感悟的世界_参考网

感悟的世界

2009-11-09邹皆恩

现代教师与教学 2009年5期

关键词：学习评价

邹皆恩

【摘要】本文介绍及论证了一种新的教学方法,博识感悟性学习。顾名思义,感悟性学习与经验性学习是相对的一种概念。前者重视灵感性激发,后者重视设定问题的方法技巧。本文介绍感悟性学习的方案设计及意图,并简介了评估方法。

【关键词】感悟性、经验性、学习、评价

The feeling becomes aware world

Zou Jieen

【Abstract】This article introduced and has proven one new teaching method, learned feeling perception study. As the name suggests, feels the perception study and the empirical study is the relative one concept. The former takes the inspiration stimulation, the latter takes seriously to establish the question the method skill. This article introduced that the feeling perception study the project design and the intention, and have introduced the appraisal method.

【Key words】Feels the perception, empirical, the study, the appraisal

请看下列三个教学设计:

Ⅰ、直线外一点,直线与点的最终的位置关系可能是

①_______________________

②_______________________

Ⅱ、①画一个棱长为1cm的正方体(各种角度),然后保持体积不变,适当变形

②在正方体一个面上点一个点,并用字母或数字标出它的位置。

③把这个正方体的各面展开成平面,你希望设点的面是哪块?

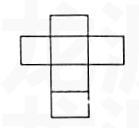
④看下面的分割平面,画出第六个分割平面的位置。

Ⅲ、①一个孤寡老人一生活了80岁,平平淡淡,无功无过,死后要求他人埋在路边。不久坟上长出一棵柳树,很多人都在树下歇凉。时间长了,坟头被人踏平了,光滑了。没有人想起这曾是一座坟,只想起有棵柳树。坟头踏成了平地。

②每只风中的鸟都栖落在迎风的枝头上。

③菜做咸了,要加点糖,而不是随意加水。

④e^iπ+1=0 包含的数学之美。

⑤如果冬天说:“春天在我心里”,谁会相信它的话呢?(纪伯伦《沙与沫》)

上述三种设计,就是博识感悟学习计划的教材。

Ⅰ.称为对称性转换,它的功能在于让学习者思维结果,放置在一个对称的空间,相互指认,相互映衬,然后打破平衡,重建智能参照体系。做到有破有立,有为有弃。

Ⅱ.称为格式训练,主要目的是为了整理学习者已有的认知与经验信息,清除无用的陈旧的杂乱的东西,变得高效而简洁。具体表现为在熟识的经验认知中形成变异机制,通过拓展认知范围,虚拟新认知空间。用两个成语能概括它的特点:温故知新、点铁成金。

Ⅲ.称为模型解读,依次为精神(人物)模型、物趣模型、事实模型、数理模型和语言模型。模型解读就是为了锻炼学生的发现、阐释能力,寻求论证路径,激发颠覆前人理论的勇气。

感悟性学习是相对于统一教材和固定教师传授解读的经验性学习。经验性学习的优势在设定的已知空间非常有效,也就是所谓的经验只能在经验中存活,而感悟性学习追求发现的是人的潜能或者说创造意识,它无法完全在知足的经验中完成,它必然要在残缺的经验中创造“经验”,在非对称的信息中反馈“信息”,在有限的技术中复制“技术”,这也就是对称性转换、格式化训练、模型解读的由来。

对称性转换强调的是思维结果的对应性呈现,用信息的虚拟对称来弥补经验的不足,这里主要给人以智力上的自信。具体说来,对称性转换涉及面较广,牵扯方方面面的知识,但都是习知和常识性的东西,它的深广都在于训练者的组合。针对六大项能力的训练是其重点,这六项能力是抽象概括能力、判断辨析能力、分析综合能力、归纳演绎能力、联想想象能力和直觉顿悟能力。当然这些能力不可能在一次训练中都体现出来,但它能够通过独特的视角,新颖的构思,灵活的评价和科学的操作实现这些能力。

格式化训练,类似于经验学习中的课堂训练,它设计的技巧在于理清经验间逻辑关系,将其概括为三种:经验空间的因果关系,交叉空间的条件关系和未知空间的假设关系。它的训练目标是在熟识经验中把握变异,即把常态转化成异态。在变异中寻求规律,即将异态转化成模型。所以格式化的目的就是建模,因而它通常有四个步骤,最后的步骤会归结为一种模型——极富典型的个例,用其涵盖知识,蕴藏经验,容纳方法。

模型解读,重点解读知识的本质内涵,提示客观世界存在的各种关系及本质联系。

如本文开头所举个案的解答会有多种多样:

Ⅰ、直线与直线外一点的关系在欧氏几何中限定的,而几何空间的变异性,却无法体现出来。这道题重点培养学生的联想与想象能力的,所以它的参考答案为,直线不“直”,直线要变曲线且闭合,也就是说,这条直线是完全画在地球表面上的。那它的两种关系是什么样,学生自然知晓。另外把侧重点关注在点上,直线看成光线而点是太阳或黑洞,那它的位置关系又可猜想。也许有人会说,把数学的高度抽象的公理约束下的概念“偷换”了,敷衍到具体的物了,最终有何意义?笔者认为,这是多数教师共生的疑窦,属于自然的,只是多少年来,不懂得思维的“对称性”的真切意义:即有抽象概括必有具象细节,有判断辨析必有模棱两可,有分析综合必有直觉顿悟,这才是辩证唯物主义认识论的本质。总想让人时时刻刻清醒或聪明,那是天方夜谭。正因为这种错误的理念,让很多人掩饰、伪巧,而不能正视自己、正视现实。人的最高智慧,是看清自身的智慧,而不是别的。

Ⅱ、格式化训练的设计意图是这样的:

①同一事物的外观在不同的角度,所展示的形态是不同的,因而,常见的形态,也非就是唯一的本质形态。这便是在熟识中开始变异。

②在正方体上点一个点,并用字母或数字标出它的位置,还需要条件,即正方体的八个顶点,由哪个作为参照系。其实这是在经验性学习中不常见的。因为经验性学习中必然要给出参照点,然后才让求点的位置坐标,也就是说这一点的坐标有两种可能。然而八种可能又可分为两大类型:即坐标原点,在点所在面和对面。其中所包含的数序与符号的规律性变化。这项“作业”的目的,告诉学习者,当我们对某些问题存在疑惑时,其根本的原因有二:第一,我们不知它们的原始参照,第二,我们不会去分类。这实际上告诉我们,事物的非常态意义,很多时候是参照系起了变化,或者说是研究方法改变了。接受变异,是创新的第一步。

③把这个正方体各面展开成平面,其时,所有的问题都简化成同一问题——这就是科学存在的全部秘密,消除表象的差异,找到本质的同一切面。之所以很多人不理解爱因斯坦的相对论,是人们总想将他的学说回归到自己的表象感知中去的缘故。这道题设计意图是当你有权决定智能表现的时候,而对他人来讲,有可能是永远的谜。当你感到自己愚笨的时候,恰恰说明你已经走出个人庸俗的经验了。这是多么值得庆幸的事啊!反过来,总认为自己很聪明,很能干,很了不起。也许,真实就是这样,可只不过是在自己的特长和经验中耍小把戏后的沾沾自喜罢了。

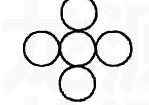
④这项作业是一种建模,最优的答案是在外面象征性地画一个大圆,均衡地罩住,为何?模型是均衡性的产物,并且它是一般性的均衡,那么这里面有哪些均衡呢?至少它包括了:知识与经验的均衡,精神与情感的均衡,感性与理性的均衡,直觉与逻辑的均衡,共性与个性的均衡。也许用“统一”比“均衡”好。统一是纸的这一面与另一面,而均衡则不然,它是孩子眼中的太阳和月亮,是自主式的“均衡”。因为人的心智不能正常发挥的原因,是由于人的感知盲点太多,焦虑、贪多、图便捷、急功近利、爱惜面子、胆怯懦弱、自卑自弃,这都是心智形成的大敌。

Ⅲ、模型解读重点解决各种关系。所谓的关系就是路径,其中最重要的是解决人与世界(精神)、主体和客体(物趣)、思维与存在(事实)、合规律性与合目的性(数理)、语言与实在(语言)、自由与必然(技术),这也就揭示了知识的奥秘:找出一切存在的相互关系,并能驾驭、顺应、遵守和崇仰。这便是知识的真正内涵。模型解读正是基于这一认识去设计的。

①无论你是无意或刻意,世界往往用其唯一的手段对你。

②倘若你是风,你是树,要从这两个角度

⑴没有我,你不能飞得更美。

⑵哪一枝都是我的枝,可只有一枝适应于你,迎风栖落,不要指望哪一个树枝会保护你,它们在风中乱舞时有可能会伤害你。

③人不能将伪装和改换的事实作为解读的对象:当靠水来稀释咸度,其他的味道也同时被稀释了。

④简洁体现了善,全面体现了真,用形式的求证解读本质。

⑤我从不敢说自己是什么,我只知道自己是在去做什么。同类无语、同质无言。世界上最美的语言,是兑现后再去看到的诺言。

模型解读不同于对称性转换之处,同一材料,同一对象能无限性地去做,而对称性转换却不能,它需要新颖而快捷,它也不同于格式化训练。模型解读既重视知识的逻辑生成,也重视知识的直觉生成。而格式化训练,只体现知识的逻辑生成。三种训练各有侧重,相辅相成。

感悟性学习的效果检测,运用两个简易公式:

①I(x₁x₂)=kx₁/x₂(k为系数)

②E(x₁x₂)=x₁x₂/k(k为系数)

公式①中,x₁为自解概念个数(自主解释),