一种改进的数据流分析方法

吕怀莲

[摘要]首先讨论传统的数据流分析技术;然后在引入分支依赖分析方法的基础上,对广泛应用于工程中的迭代数据流方程求解方法进行分析,提出一种改进的数据流分析方法,并将其应用到实际的程序分析中。

[关键词]数据流分析数据流方程控制流语句块

中图分类号:TP6文献标识码:A文章编号:1671-7597(2009)0710059-02

一、引言

基于源代码静态分析的数据流分析[1][2]作为程序分析的一种重要技术,能够从程序代码中收集程序的语义信息,它不必实际运行程序就能够获取程序运行时的信息,更易于人们理解和分析程序,因此被广泛用于解决编译优化、程序验证、调试、测试和并行编程环境等中的问题。

数据流分析获取信息的方法有两种,对于结构化的程序可采用语法制导的求解方法,对于任意控制流的程序可采用迭代数据流方程求解的方法。迭代数据流方程求解方法首先要建立控制流图,然后为每个控制流图结点建立数据流方程,最后通过迭代求解数据流方程来获取数据流信息,这种方法也被称为到达-定值的迭代算法[1],在实际的工程中应用较广。到达-定值迭代算法需多次迭代计算控制流图上所有结点的定值信息[3],时间复杂度较高。本文提出一种可应用于一般数据流分析的改进方法,在最小的迭代求解范围内以最小的迭代次数可获取完整准确的数据流信息。

本文通过引入软件测试中分支依赖“语句块”的划分思想粗化分析粒度,对传统的迭代数据流方程求解方法进行改进,将控制流图上所有结点定值的迭代求解过程转化为局部的对循环语句块内结点定值的迭代求解过程。最后,对改进方法进行分析和对比并将其应用到实际的程序分析中。

二、迭代数据流方程求解方法及其改进思想

(一)数据流方程及其建立

对于每个语句对应的控制流图结点N,可以定义out[N],kill[N],gen[N]和in[N],其中gen[N]为N对应语句处产生的定值集合,kill[N]为N对应的语句在程序中注销的定值集合;in[N]为N对应语句前一点到达的定值集合,out[N]为N对应语句后一点到达的定值集合。并且,产生和注销的信息依赖于所需要的信息。若每个控制流图结点的gen和kill已经计算,则可建立如下两组方程:

(2-1)

其中,P是N的控制流图中的前驱结点。第一组方程表明,进入语句开始点的定值是所有前驱结点到达的定值集合的并;第二组方程表明,控制流通过一个语句时,语句末尾的定值是这个语句产生的定值,或是进入语句开始点并且没有被这个语句注销的定值。这样的方程叫做数据流方程。如果控制流图有n个结点,则从(2-1)可建立2n个方程。

(二)到达-定值迭代算法和语句块

到达-定值迭代算法反复计算这2n个方程,直到所有结点的in和out集合都不再改变(即每一个控制流图结点都到达平衡状态)。每一次的迭代求解都要对所有结点的in和out重新计算一次。

到达-定值迭代算法求解过程中,循环结点及其内部循环语句结点不能到达平衡状态,导致了求解过程的多次迭代。对一个完整的控制流图,循环结点一定存在一个不满足循环条件(False分支)的出口,否则,该循环将陷入死循环而导致控制流图的不完整。因此,本文通过“封装”循环结点及其内部循环语句结点来简化数据流方程的迭代求解过程。到达-定值迭代算法的数据流分析方法是基于语句级别的程序分析。在软件测试中,静态分析技术——分支依赖分析是以语句块为分析粒度的程序分析。分析粒度从语句级别粗化到语句块级别,有助于获取语句块之间的依赖信息。

基于分支依赖分析中分析粒度可以粗化这一思想,本文将求解过程中遇到的循环结点及其内部结点“封装”成一个整体,称作为一个循环语句块,即沿着循环结点满足循环条件(True分支)出口构成的环上的所有语句结点组成的集合。对控制流图而言,循环语句块可被看作是一个虚的语句结点,该语句结点的迭代结果即为循环语句块中的循环结点到达平衡状态的迭代结果;而对循环语句块的内部结点则是一个多次迭代数据流方程求解的过程。获取循环语句结点最终的定值迭代求解结果后,沿着循环结点的False分支继续进行数据流方程求解。由此,可以认为最好情况下只需一遍迭代数据流方程求解即可使控制流图上所有结点到达平衡状态。

含循环结点的循环语句块(以while结点为例)的提取方式和数据流分析过程如下:

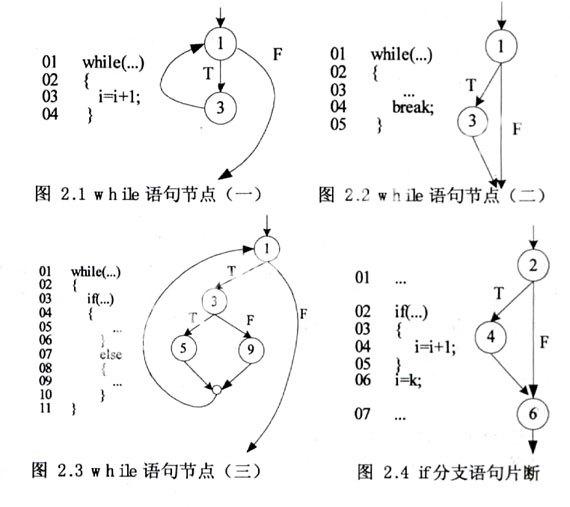
1.基本while语句结点(见图2.1)

图2.1中,结点1和结点3构成环,因此结点1和3构成一个循环语句块。根据结点1的第一次定值求解结果对该循环语句块进行到达-定值迭代求解,直到结点1和结点3到达平衡状态。此时结点1的最后的迭代结果即为该循环语句块的最终求解结果。

2.含break的while语句结点(见图2.2)

图2.2中,由于出现break结点,沿着结点1的True路径找不到环,即该图上没有结点构成循环语句块。因此只需将图中的结点按照一般语句的求解过程求解即可。

3.含分支结构的while语句结点(见图2.3)

图2.3中,沿着结点1的True分支找环,结点1、3、5、9构成一个循环语句块。根据结点1的第一次定值求解结果对该循环语句块进行到达-定值迭代求解,直到结点1、3、5、9到达平衡状态。此时结点1的最后的迭代结果即为该循环语句块的最终求解结果。

(三)分支结构和迭代求解次数

图2.4是一个if分支语句片断,结点6的定值计算可以先于结点4计算,也可以在结点4的定值计算后进行。但是,结点6的定值计算依赖结点4的定值求解结果,因此,对整个程序片断,前一种计算模式将比后一种的求解迭代次数至少多一次。而且,随着分支结构或分支嵌套的增多,求解的迭代次数将急剧增大。由此可见,分支结构上语句的定值求解顺序直接影响整个程序的定值求解迭代次数。

由上面讨论可知,分支汇合结点的定值依赖于分支上结点的定值求解结果,因此,利用控制流信息,确立分支结构上结点的定值计算先于分支汇合结点定值计算的求解模式,能够有效避免最大迭代次数的出现。

(四)到达-定值迭代算法的改进算法

基于2.2节和2.3节的讨论,可得到如下由算法1和算法2组成的改进算法。算法1是主入口算法,基本思想是对循环结点首先沿着它的True分支找环,并且定值的迭代求解只在环上进行;之后沿着它的False分支继续定值求解。算法2是对含循环结点的循环语句块中所有结点定值的求解。

其中,控制流图是一个有向图,它的每条边都连接有两个结点:头结点和尾结点,每个结点(开始结点和结束结点除外)都有至少一条入边和至少一条出边。并且,2.3节的讨论包含在算法1步骤3中“选择下一个可分析的结点”的操作中。

三、实例分析和方法对比

通过实例分析对比到达-定值迭代算法及其改进算法,两者的求解结果是一致的;并且,改进算法利用语句块划分思想和控制流信息将迭代求解局限于循环语句块内部,对程序整体而言,只需一次迭代求解即可获得所需的数据流信息。循环语句块内部的中间迭代求解结果无需保存,空间复杂度不会高于到达-定值迭代算法。实例分析对比结果,改进算法时间开销只是到达-定值迭代算法的最好时间开销的一半左右,由此可见,改进算法比到达-定值迭代算法更高效。并且,改进的数据流分析方法在求解过程中有以下几个优点:

1.全局的数据流迭代求解过程被转化为局部的迭代求解过程;

2.粗化分析粒度,引入了语句块的划分思想,获取数据流信息的流程更加清晰;

3.利用控制流信息确定求解顺序,确保以最小的迭代次数获取数据流信息。

四、结束语

数据流分析作为一种非常重要的静态程序分析技术,在保证软件质量与可靠性方面起到重要作用。本文通过引入软件测试的部分思想,对广泛应用于工程中的传统数据流分析方法进行了分析,提出了一种可应用于一般数据流分析的改进方法,该方法通过粗化分析粒度和利用获取的控制流信息,在最小的迭代求解范围内以最小的迭代次数获取完整准确的数据流信息。该方法已应用到安全检查工具XDCHECKER中。实践证明,该改进方法能够有效地进行数据流分析。

参考文献:

[1]Alfred V.Aho,Ravi Sethi,Jeffrey D.Ullman.Compilers:Principles,

Techniques,and Tools.Reading,MA:Addison Weslsy Publishing Company,1986:279-316.

[2]Flemming Nielson,Hanne R.Nielson,and Chris Hankin. Principles of Program Analysis.Springer-Verlag New York,Inc.,Secaucus,NJ,USA,1999.

[3]Gleb Naumovich.Using the Observer Design Pattern for Implementation of Data Flow Analyses.ACM SIGSOFT Software Engineering Notes,2003;28(1):61-68.