“能赶上火车吗？”教程分析

刘全兴

一、联系生活,巧妙入境

导思题:小明是一位导游,正带着7位游客分别乘两辆小汽车(每辆四人,含司机5人)在外地旅游,玩得很开心,突然小明接到他所在旅游公司的电话,电话称现在是旅游旺季,旅客太多,旅客的返程火车票很难买到,现好不容易买到当天下午6点的返程火车票,要他连旅客马上赶往火车站,小明挂上电话,马上组织游客赶往火车站,当小明赶到一条样板示范路(管理极严,中间无红灯)的路标时,不幸一辆小汽车发生故障,小明很着急,看看表,已是下午5点18分,他朝四周看看,见路标上写着距火车站15千米,限速60千米/小时,聪明的你可一定帮小明想办法及时赶到火车站哦(要知道完不成任务,旅游公司损失可就大啦)。

二、合作交流,激励解题

为了提高学习效率和激励学生解题热情,决定进行分组讨论,并制定各小组每提出一种方案(可行)奖励500分,答错不扣分,一下子把学生的热情调动起来,唤起了学生的竞争意识和创新意识。

三、探索比较,明晰思路

1. 提出问题,抓住关键题设

距火车站15千米,有一辆小汽车可用,限速60千米/小时,8人(连导游)要赶到火车站,还有42分钟。

2. 循序渐进,由算术解法自然而然过渡到方程解法

方案一:分两批送人到火车站,4人在故障点等车,a让车(开得最快)开到火车站后返回来接后面的4人。(如图)

计算:3×15÷60=0.75小时=45分钟,不可能及时赶到火车站。

方案二:(联系生活实际,发挥人的能动性,敢“破”敢“立”)有学生提出可以让后一批人先走一段路,再在车返途中接应,(立)假设人的速度为5千米/小时,车开得最快60千米/时。(如图)

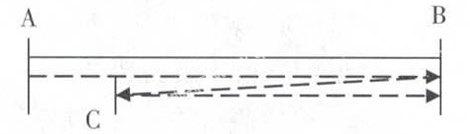
学生分析能赶到和不能及时赶到的原因时:认为AC距离要适当,但事先不知道,只能设x千米。(自然而然过渡到方程)

AC=x千米,分析如何找出等量关系:人走AC段的时间=车走AB段+BC的时间,即x/5=(15+15-x)/60,算出x=30/13千米,从而t≈40.4分钟,可及时赶到火车站。

3. 问题的再深入

方案三:有学生提出可以让后批旅客先走一段路,到火车站前放下头批旅客,也让他们走一段路,车再返回路途中接应后批旅客,这样可以更节省时间,假设人的速度为5千米/时。

用方程组解,开始有困难,但学生很快取得突破,取得突破的关键是优化了两个条件:①车速=60千米/时=1千米/1分钟,车走的路程千米数=分钟数,②人速:车速=1∶12,同时间内人车路程之比=1∶12。

解:设AC=x,BD=y①13x+2y=15×2,②13y+2x=15×2,由①+②得:15(x+y)=60,从而(x+y)=4千米,车在往返(三个)全程45千米中少走8千米,即车实际走37千米,马上得到t=37分钟,可及时赶到。

方案四:假设人跑步速度为8千米/小时,开得最快60千米/小时,算法如上,学生们对速度为8千米/时展开激烈的争论:一方认为8千米/小时不合理,理由是旅游太累、又有行李;另方认为8千米/小时合理,理由是情急之下,人的潜能无限(教师都以予正面肯定)。

四、类比联想,探索问题(策略的开放,由定性再到定量)

1. 有的学生提出等车(的士)可解决问题,继而有学生提出要求在27分钟内等到车(15千米需用15分钟,只能用27分钟等车)。

2. 有的学生提出修车可解决问题,同样继而有学生提出要求在27分钟内修好车(15千米需用15分钟,只能用27分钟修车)。

3. 学生提出拖车方案可解决问题:先找绳,拖车考虑到减速到30千米/小时,但又未考虑到拖车不能载人的交通规则。

4. 更有的学生认为不着急,火车票有3天的期限。

五、归纳总结,促进建构

结合板书让学生说说本节课学到的知识,并说出是怎样学到的,目的是让学生对本节课所学的知识系统有所认识,培养学生整理知识的能力。

最后由各小组讨论得出可行的方案:让前后两批人走一段路,时间可以控在37分钟至42分钟,能赶上火车。

责任编辑罗峰