基于最小时延差的多播路由中心点选择算法

李　萍

[摘要]研究分析各种中心点选择方案对中心树的时延和时延差的影响。首先证明寻找时延和时延差受约束的中心树问题是NP完全问题,然后提出一种可以使时延差较小的中心点选择算法。

[关键词]计算机网络 多播路由 动态多播路由算法 多播路由协议 中心点选择

中图分类号:TP3文献标识码:A文章编号:1671-7597(2009)0920092-01

随着网络技术的发展,应用于多媒体会议、远程教育、数据分发等实时业务的多播通信成为当前研究最多,和应用最广泛的网络连接方式。目前,单目标和多目标多播路由问题仍是路由问题研究的一个热点。

一、分布式中心点选择研究

在分布式网络(例如互联网)中,网络的拓扑结构也是由网络中所有节点分布式掌握,因此没有一个节点掌握全部拓扑结构。为此,一个理想的中心点选择算法应该在每一个节点只需要一部分信息,并且与邻节点的交互也应该尽量少。HILLCLIMB协议步骤如下:(l)初始时,多播组只有一个成员,因此它就成为中心点,然后周期性地运算以下步骤;(2)启动计时器Tl,Tl计时到就开始搜索;(3)发起搜索的节点向邻节点发送组成员和源节点列表,询问它们的权值,重新启动计时器TI,以便在以下步骤中有消息丢失时算法会重新从步骤(3)开始;(4)每个邻节点根据选择函数计算权值应答;(5)发起搜索的点根据最新消息更新n个最佳中心点;(6)若搜索点的权值小于邻节点的最小权值,则转移到步骤(11);(7)若所有最佳邻节点已在路径列表中,则转移到(11);(8)搜索点将自己加到已访问节点列表中;(9)搜索点从未访问的最佳邻节点中选取最佳的一个节点作为下一个发起搜索的节点;(10)上一个搜索节点将路径列表、组成员和源节点列表发给新的搜索节点,然后转到(3);(11)最后的搜索点向中心点发回一个消息报告它的权值,中心点是路径列表中的第一个节点;(12)最后的中心点成为新的中心点,然后转到(2)。

二、一种优化时延差的方案设计

对于时延受约束的中心树问题,最小最大直径方案(MinMaxDiameter)

应该是最合适的,因为此时的目标是限制最大时延,使之小于约束值。而最小平均距离方案并不合适,因为我们并不关心平均时延,只要最大时延约束值小于约束值即可。分析最小最大直径方案,可以发现可能会出现有些成员的时延较小,从而导致时延差比较大。最小平均化方案也不能解决这个问题。为此这里首先提出一种方案,该方案的基本思想如下:

步骤1:首先以任一节点为中心点,求多播树最大时延,若最大时延小于约束值,则求出时延差,然后加入中心点集合;

步骤2:将中心点集合中时延差最小的节点作为中心点。方案称为优化时延差方案,将该方案称为OVET(nelayvariation Based CenteredTree)。

通过该方案选择的中心点成员以最短路径连到中心点即可使时延差较小。当然优化时延差方案并没有使得时延差受到约束,这个问题可以使用以下方法解决,即欲加入的成员不是通过最佳路径连到中心树,而是求到中心树各节点的最短路径,选取一个最佳的作为中间连接节点,但这样做会带来一个问题,即失去了中心点选择的意义。因此上述方案不是一个时延差约束问题DVBCT的解决方案,而是尽可能减少了时延差。以上方案基于网络组成员节点来选择中心点。本章主要关注中心点选择,因此对路由选择采用了固定的算法——最短路径算法,从而来比较

不同中心点选择算法的性能。

三、仿真模型和仿真结果

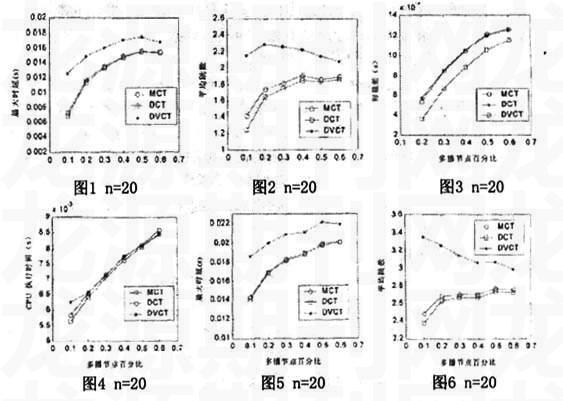
对一定大小的网络规模产生200个网络,在每个网络上进行20次试验,每次试验随机选择m个成员多播组进行仿真,m为0.1n-0.6n之间变化,因此每一个仿真数据对应4000个实验数据。仿真数据的置信度为95%,置信区间不超过5%。时延根据节点间的距离和信号在光纤中的传播速度为2/3光速算得。这里仿真的网络大小分别为n=20,50,网络平均节点度数为4。这里将比较最小化时延差方案DVCT、最小最大直径方案DCT和最大中心树方案MCT的时延、平均跳数、时延差和计算时间。图1～4是网络节点数为20,平均节点度数为4时各算法的最大时延、平均跳数、时延差和计算时间的比较。图5～6是网络节点数为50,平均节点度数为4时各算法的最大时延、平均跳数、时延差和计算时间的比较。

由图1～6可见,DCT的最大时延最小,DVCT的最大时延最大,MCT的最大时延略大于DCT的最大时延。这是因为在这里只考虑时延,DCT使最大直径最小也就是使时延最小,MCT的最大距离也是与时延紧密相关,因此其时延较小,而DVCT由于只考虑使时延小于约束值,并没有使之最小化,因此它的时延最大并不为奇。综上所述,DVCT是时延约束的、时延差较小、且执行时间与DCT、MCT算法相当的算法,可适用于时延约束且时延差较小的场合。

四、结论

本文着重讨论了中心树和中心点的选择。综述了现在学术界对中心树和中心点选择的研究进展,然后分析了现有的中心点选择方案,提出了尚未有研究的时延和时延差受约束的中心树问题,并证明它是一个NP完全问题,最后针对这一问题,提出了一种优化时延差的方案,即DVCT方案。对DvCT的仿真结果表明它是一种时延受到约束的、时延差较小、计算复杂度与MCT、DCT相当的一种算法,可适用于对时延差有要求的场合。

参考文献:

[1]曹佳、鲁士文,应用层组播的最小延迟生成树算法,软件学报,2005,16(10):1766-1773.

[2]李帮义、姚恩瑜,最短路网络及应用,系统工程理论与实践,2000,6:104-107.