对正午太阳高度的理解与应用

王彩琴

【摘 要】 正午太阳高度角的变化,影响着人类的生产和生活。对正午太阳高度的理解与应用是教学的重点,也是难点。这部分内容常常是考试的切入点,考查学生运用地理基本原理、规律分析、解决实际问题的能力。所以,在学习中应予以高度重视,从本质上理解和掌握正午太阳高度的变化规律,以及正午太阳高度角的计算方法,运用它解决生产和生活中与之相关的问题。

【关键词】 正午 太阳 高度 变化 应用

一、理解概念

1. 太阳高度:是太阳高度角的简称,表示太阳光线对当地地平面的倾角。它在很大程度上决定地面获得太阳热能的多少。

2. 太阳高度的变化

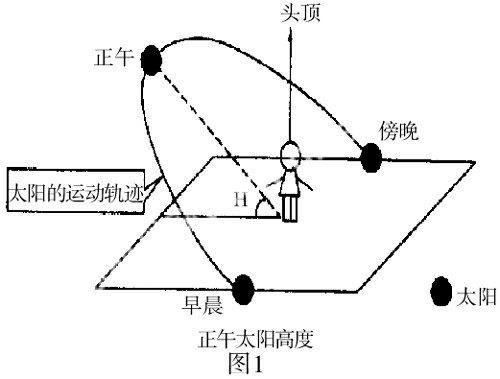
在一日内,太阳以不同的高度照射地面。从早晨日出到傍晚日落,太阳高度先是由小变大,然后由大变小。正午时刻,太阳升得最高,称为正午太阳高度(此时,各地地方时是12时)。如图一所示

说明:

(1)晨昏线上(日出日落)太阳高度=0°;昼半球上太阳高度>0°;夜半球上太阳高度<0°。

(2)正午太阳高度是一天中最大的太阳高度,但是并非一定就等于90°,只有当太阳直射某一纬度时,该纬度的正午太阳高度才能达到90°。我们知道太阳直射点所能达到的纬度范围是23°26′N～23°26′S之间,那么在这一范围之外,其他纬度正午太阳高度均小于90°。

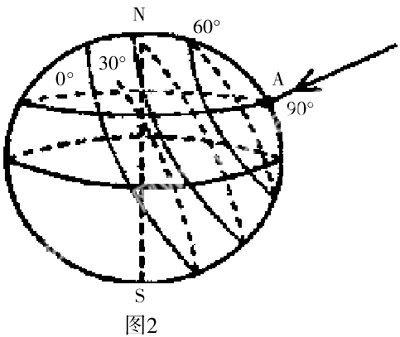
(3)从全球范围来说,在太阳直射点上,太阳高度是90°,从直射点开始,太阳高度向四周降低,作同心圆分布,到晨昏圈上,太阳高度为0°。如图二所示

二、正午太阳高度的变化规律

正午太阳高度是一天中最大的太阳高度,它的大小随纬度不同和季节变化而有规律的变化着。

1. 正午太阳高度的季节变化规律

(1)夏至日:太阳直射北回归线,北回归线及其以北各纬度,正午太阳高度达一年中最大值;南半球各纬度,正午太阳高度达一年中最小值。

(2)冬至日:太阳直射南回归线,南回归线及其以南各纬度,正午太阳高度达一年中最大值;北半球各纬度,正午太阳高度达一年中最小值。

(3)春分日和秋分日:太阳直射赤道,赤道上正午太阳高度达一年中最大值;正午太阳高度自赤道向两极递减。

2. 正午太阳高度的纬度变化规律

同一天,正午太阳高度由太阳直射点所在纬度向南北两侧递减。

夏至日:太阳直射北回归线,由北回归线向南北两侧递减。

春分日和秋分日:太阳直射赤道,由赤道向南北两侧递减。

冬至日:太阳直射南回归线,由南回归线向南北两侧递减。

三、正午太阳高度的计算

正午太阳高度在太阳直射点上是90°,由太阳直射点所在纬度向南北两侧递减。某一地方正午太阳高度的大小,可以用公式H=90°-|φ-δ|来计算,公式中H为正午太阳高度,φ为当地地理纬度,永远取正值,δ为直射点的纬度,当地夏半年取正值,冬半年取负值。

由于任一地点正午太阳高度与直射点太阳高度的差值等于它们的纬度差,在实际解题中,为了计算方便,把绝对值去掉,简化成H=90°-某地纬度与直射点纬度的纬度差。

四、正午太阳高度的应用

1.计算热水器安装角度

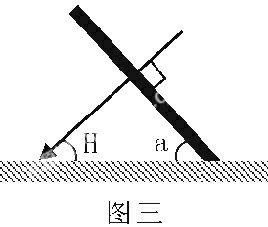
基本原理:要最大限度的利用太阳能资源,应该使太阳能热水器集热面与太阳光线垂直,提高太阳能热水器的利用效率。如果太阳能热水器集热面与太阳光线垂直,那么热水器集热面与地面之间的夹角就等于当天正午太阳高度角的余角,也就是太阳直射点与当地地理纬度的差值。如图所示,在图八直角三角形中,某天的正午太阳高度角H=90°-|φ-δ|,则а=90°-H=|φ-δ|。

案例探究:

某校所在地(120°E,40°N)安置一台太阳能热水器,为了获得最多的太阳光热,提高利用效率,需要根据太阳高度的变化随季节调整其支架倾角,下列四幅日照图中与热水器安置方式搭配不合理的是

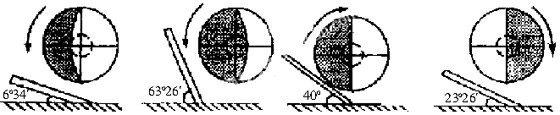
解析:D.根据图中地球自转的方向和晨昏线特点,判断四个图所对应日期(A图为夏至日,B图为冬至日,C和D图为春分日或秋分日),再根据正午太阳高度的计算公式H=90°-|φ-δ|可计算出H1=73°26′,H2=26°34′,H3=H4=50°;第三步根据支架的倾角和正午太阳高度角应该互为余角时,搭配合理,推出只有D项不合理。

2.计算楼房间距

基本原理:为了使楼房底层获得充足的太阳光照,一般来说,纬度较低的地区,楼距较小;纬度较高的地区,楼距较大。解题关键是计算当地冬至日的太阳高度,并计算影长。

案例探究:

如图所示,位于北纬36°34′的某疗养院,计算在一幢20米高的楼房北面新建一幢楼房。因为疗养的需要,要求高楼的每一层一年四季都能晒到太阳。

(1)新楼至少要距原楼多少米?

(2)若黄赤交角变为23°34′,两楼之间的距离将应如何变化,才能保证各楼层均有较好的采光?

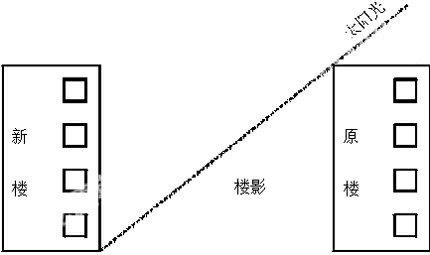
解析:根据题意因疗养院位于北纬36°34′,当太阳直射南回归线时北半球正午太阳高度角达一年中最小值,若此时该楼的一层能被太阳照射的话,则各楼层都能被阳光照射,求出此时的正午太阳高度角H=90°-|φ-δ|(代入φ=36°34′,δ=-23°26′)即H=30°.根据三角函数关系,两楼间最小距离应为x=20cot 30°,x=34.7 m。若黄赤交角变为23°34′,比原来变大,则此时北纬36°34′的正午太阳高度角H′=90°-|φ-δ′|,H′=29°52′变小,但x=20cot 29°52′在(0°～90°)为减函数,故两楼间距应增大。

答案:(1)34.7 m (2)间隔应增大

3.确定房屋的朝向

基本原理:为了获得充足的太阳光线,确定该房屋的朝向与正午太阳所在的位置有关。在北回归线以北的地区,正午太阳位于南方,房屋朝南。在南回归线以南的地区,正午太阳位于北方,房屋朝北。

4.确定地方时

当某地太阳高度达到一年中最大值时,此时当地的地方时是12时。

参考文献:

[1]金祖孟.地球概论(第三版).北京:高等教育出版社,2000

[2]全日制普通高级中学教科书(必修)地理上册.人民教育出版社,2003

(责编 李 晔)