通过数学模型培养学生解决问题的能力

李爱娜

当今是数学广泛应用的时代，随着社会的发展，科技的进步，特别是信息时代的到来，数学模型的地位也得到显著的提高，数学模型不仅是数学学科的背景材料，它已成为人们改造自然的一种技术。千姿百态的数模型，闪烁着人类智慧的无限光芒，数学模型的应用遍及科学、工程、经济、语言乃至历史考古，计算机的出现更使数学模型插上飞翅，获得实时控制的实用效果。

一、什么是数学模型

数学模型乃是问题从数学角度的抽象化，一般说来，一个有价值的问题，进行数学化，通过分析、求解、研究，都会抽象成一个数学模型，成为一类问题求解的模式。广义地理解，一切数学概念、法则、公式、定理、数量关系、数学事实(各种方程、函数式等)都可以称之为数学模型。

现代数学观认为，数学具有科学方法论的属性，数学思想方法是人们研究数学、应用数学、解决问题的重要策略。而建立数学模型，研究数学模型，正是问题解决过程中的中心环节，是决定问题解决程度如何的关键。当年，瑞士大数学家欧拉面对哥斯尼堡“七桥问题”时，巧妙地将陆地看成点，将桥看成线，把实际问题转化为点线相连的数学一笔画问题，通过对所构建的模型的研究，来最终解决问题，正是这一过程的绝好例证。显然，在这个问题解决的过程中，数学家构建出的一笔画模型是关键，体现出了数学模型在实际问题解决过程中的作用——它在很大程度上决定了问题能否最终得以彻底的解决。

数学模型是数学基础知识与数学应用之间的桥梁，建立和处理数学模型的过程，就是将数学理论知识应用于实际问题的过程。并且，建立模型更为重要的是，学生能体会到从实际情境中发展数学，获得再创造数学的绝好机会，在建立模型、形成新的数学知识的过程中，学生能更加体会到数学与大自然和社会的天然联系。因而，在数学教学中，让学生从现实问题J隋境中学数学、做数学、用数学应该成为教师的一种共识，只有这样，数学教学中的“问题解决”才有了相应的环境与氛围。

二、教学中培养学生的模型思想

学生在学习数学知识和应用数学知识的过程往往无意识地形成很多的数学模型来解题，比如在一个小学生的头脑里，由于他解过许多算术应用题，因此已形成了相当多的数学模型，当向他提出一个算术题的时候，他略加思索就会列出算式，给出答案。如果问题超出了他的知识范围，他从自己的模型库中找不到相应的模型，而他又学得不够灵活。他就会说：没学过。如果他的思维灵活敏捷，他就会变通自己的模型来求解。中学生的头脑里储存了更多的数学模型，如“方程模型”、“函数模型”、“不等式模型”、“全等模型”、“相似模型”、“面积模型”、“几何图形模型”等等。当他面临一个问题时，他会迅速巡检自己的模型库，如果找不到可直接应用的模型，他会通过式子变化、参数代换、引辅助线、对问题进行等价变换等，转变为已有的模型来求解。

学生既然自己也能无意识地利用数学模型，教师何不加以有意识的指导以培养学生的模型思想，比如在讲解实际问题时不要只分析解题过程，多讲一些解题过程的解题方法及形成解题方法的思路，方法中应用了所学过的哪一数学模型，用这一模型还能去解决什么问题等。

下面，以一道例题教学为例：

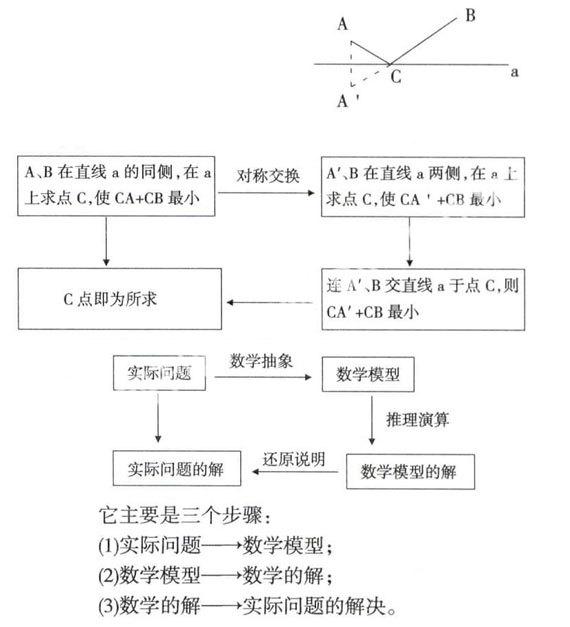
如图，在铁路a的同侧有两个工厂A、B，要在路边建一个货场c，使A、B两厂到货场c的距离和最小，在图上作出点c。

[1]思路分析：

[2俐用例题变式，渗透模型思想方法：

变题1：A、B为直线a同侧的两个点，试在a上求c、D两点使cD=b，且使折线AcDB为最短。

变题2：河的两岸成平行线，A、B分别为河两侧的两个点，问应在何处建桥(桥应垂直于河岸)，才能使从A至B的路程最短?

三、培养学生应用自己的数学模型解决实际问题

数学模型不同于一般的模型，它是用数学语言模拟现实的一种模型，即把一个实际问题中某些事物的主要特征、主要关系抽象成数学语言，近似地反映客观事物的内在联系与变化过程。建立数学模型的过程就称为数学建模，数学建模的思维过程可用下面的框图表示：

它主要是三个步骤：

(1)实际问题——数学模型；

(2)数学模型—一数学的解；

(3)数学的解—一实际问题的解决。数学模型呈现的形式是多种多样的，有的以函数显示，有的以方程显示，也有的以图形显示，当然还有其他各种形式的模型。下面举常用的数学方程模型加以说明：

笔者刚想训斥学生，没想到一个平时调皮学生最后一个过去，一声不响的把地上的篮球收拾得整整齐齐。笔者当时真的被感动了，马上在全班学生面前表扬了他，全班同学也都为他鼓掌，看他被表扬时那副憨厚的样子真是可爱极了。说也奇怪，从此那个调皮学生体育锻炼更积极了，学习成绩也进步了。可见激励只有在最佳情境、最需要的时候才发挥最大的作用。

2激励要适度

激励不仅是对学生的肯定与鼓励，同时也是向其他同学树立榜样。例如，在篮球行进间单手肩上投篮的教学分析动作时，教师分别请一个动作准和一个动作错误的同学示范，然后问：“刚才两位同学所做的动作，好在哪里，错在哪里?”在学生作出了正确的回答后，教师用鼓励的语气教学，有效地促进学生在思考中练习。表扬时要做到言如其实、恰如其分。过轻的表扬让学生失望、泄气；过头的表扬有时让学生产生自满情绪，或者反过来认为你在取笑他。

3激励要讲策略

激励性评价并不是一味追求肯定，也要有艺术性否定。要采用委婉、幽默的措辞加以表达，体现对学生的尊重，更多地给予期望和鼓励，即寓贬褒，创设一种心理安全的教学氛围，使教学评价的调控功能得以有效发挥。如果教师一味追求讲“好听的话”，则会对学生人格的健全发展有一定的负面影响。很难想象，听惯了“好听的话”的学生，会怎样应对挫折，怎样明辨是非、认识自我。

六、总结反思——课堂教学有效性的助剂

高三学生所追求的精神状态是心情愉悦，心里轻松。学生在紧张的学习之余，通过体育活动松弛紧张的神经，释放学习的压力，让压抑的心情得到缓解，让疲惫的心得到休息，为进一步的奋斗做好心理的准备。为此，教师在高三期中考试前安排了班级拔河赛，在第一次高考模拟考前进行了班级跳长绳比赛，增强了班级凝聚力，陶冶情操，缓解考前压力，师生反映良好。

通过教学实践和取得的良好教学效果，笔者做出了总结反思：首先，教师要转变观念，提高自身创新意识。要研究学生的心理需求，才能超越常规，更大胆地、独特地运用有创造性的教学模式。其次，加强赏识教育，让每位学生都有机会去真正实践，去参与，真正体现出学生的主体作用。在教学中少批评多表扬、多鼓励、多肯定，营造一种宽松和谐的学习氛围。

数学模型呈现的形式是多种多样的，有的以函数显示，有的以方程显示，也有的以图形显示，当然还有其他各种形式的模型。下面举常用的数学方程模型加以说明：