深度开发学习材料 有效放飞学生思维

钱　兴

学习材料是教与学的媒介，是教师教与学生学的桥梁，如何让这座桥梁发挥最大的价值，是我们教师要考虑的问题。多年的教学实践让我体会到学习材料的开发度，对学生的思维起着很大的影响。我们要在充分尊重原有学习材料的基础上，让学习材料的内涵更加丰富，让材料中蕴藏的问题更具挑战性、探究性，让材料的功能更有效地释放。

前不久，我在海盐一所小学听课时，听到这么一则学习材料：

(1)口算，把表格填完整。

(2)仔细观察下表，你有什么发现?

此题放在了学习《长方形面积》这一课的最后，教师既把它当做新授课的巩固练习，又把它当做新授课的延伸拓展，从材料的功能性上说可谓“一举两得”。但由于时近下课，教师匆匆把它带过，学生的发现基本停留在长方形的长一定，宽增加1厘米，面积就增加8平方厘米。课后，我思索着这个材料，觉得这个材料完全可以开发。

[开发理由]

一、口算的意义不是很大。学生在学了长方形面积后，已经知道长方形的面积计算公式是长×宽，口算没有从本质上提升学生的思维。

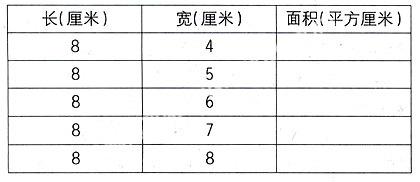
二、表格的限制使学生的学习按部就班，没有真正自主探索的空间；表格的呈现使学生的注意力放在了关注数据之间关系和寻找数据之间规律上，而忽视了内在的本质。

三、这个表格仅仅是现象中的一部分，虽然有多个例子支撑，但仍然是一些个例，不能代表全部，我们的数学不能以偏概全。一种不完全的归纳，不足以令学生信服。

回校后，我把该材料改了，当做练习课在自己班里试教。

[改后新貌]当长方形的长不变，宽变化，面积会怎么样?

[现场效果]

学生独立探究，3分钟后交流。

师：谁先来向大家汇报一下你的研究成果?

生：当长方形的长不变，宽大起来，面积也大起来。

师：你是怎么想的?能具体说说看吗?

生：我是这样想的，长×宽=长方形面积，长不变时，宽大起来，面积肯定也大起来。

师：哦!就是一个因数不变，另一个因数大起来，积也大起来，对吧!还有不同的想法吗?

生：我先举例，假设原来长方形的长是6厘米，宽是3厘米，它的面积是18平方厘米，另一个长方形的长也是6厘米，但宽是4厘米，它的面积就是24平方厘米。从例子中可以看出，宽变大，面积也变大。

师：讲得很清楚，非常棒!

生：老师!我画了一个表格，还要清楚。(实物投影展示学生表格)

生：长方形的长不变，宽大起来，面积也太起来，而且宽大l厘米，面积刚好大6平方厘米；宽小起来，面积也小起来，而且宽小1厘米，面积刚好小6平方厘米。面积随着宽的增加而增加，随着宽的减少而减少。当宽是6厘米时，正好是个正方形。

师：说得真好!用表格举例是一种好方法，表扬一下!还有别的方法吗?

生：我画图的。(实物投影展示学生表格)

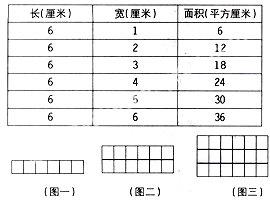
生：长6厘米就是一行摆6个小正方形，宽1厘米就是摆1行小正方形，宽2厘米就是摆2行。宽多1厘米，就是多摆一行，多6个小正方形，也就是多6平方厘米；宽多2厘米，就是多摆2行，多6×2个小正方形，也就是多12平方厘米。

生：多3平方厘米也行。(其余学生表示不解)

师：怎么想的?

生：宽大半厘米，也就是多半行，就多6个半小方格，刚好是3平方厘米。

师：真有创意，宽除了整数，还可以是其他数，那这样的例子举得完吗?

生(齐答)：举不完。

课到此，我觉得已经差不多了，开始给同学们总结了。但我的话音刚落，一只小手又举了起来。

生：老师!我有一个好办法!假设宽多x厘米，那么就多x行，也就多(长×x)平方厘米。

思考一：学习材料的开发，是否能引起学生思维真正的开放?材料的开发，如果不能打开学生的思维，那么这种开发是无效的。课上，学生的表现大大出乎我的预料。没想到去掉原题的表格限制，学生韵思维一下子打开了，学生都有自己喜欢的研究方法，有的用乘法的数量关系，有的用列式举例，有的用列表举例，有的用画图的方法，甚至有的用字母表示数。在交流汇报中，学生的认识不断加深，思维的广度和深度得到了有效的拓展和提升。在解决问题的过程中，那些即时的、感性的经验不断地合理化、系统化，进而让学生建构起自己的数学方法与思想，有效地唤醒了学生的“元认知”。

思考二：学习材料的开发，是否有利于构建创新、挑战的课堂?课堂教学是培养学生创新的主渠道，教师要培养创新人才，必须从实施课堂教学的开放做起。重视为学生提供“开放性的学习材料”，必将为学生提供更多思考与挑战的空间，更多自主探究的余地，使学生的潜能得到更极致的发挥。对比两者的教学，后者更好地促进了学生学习的主动性，为学生全方位的参与创造了条件。后者更能满足每个学生的学习需求，能更好地启迪学生的思维，使学生的创新精神、实践能力得到更好的发展。

思考三：需要开发成怎样的学习材料，才能更好地放飞学生的思维?学习材料是数学教学的基石。好的学习材料能引领出概念，能激发学生的好奇心和探索欲望，能激活学生的思维，并巧妙的吸引学生来探索问题、理解教学。笔者认为，好的学习材料应该具备下列特征：①材料是易懂的、现实的、有趣的，能吸引学生的眼球。②学习材料中提供的信息与问题有较强的挑战性和探索性。③学习材料能使学生产生多样的解法和思维，能照顾到一般和个别，能让优秀生“吃好”，让后进生“吃饱”。④学习材料能渗透数学本质，具有数学价值，能够启发学生的数学思考。⑤学习材料能承前启后，为后续的学习提供数学经验和方法。