自编歌诀，记忆性质

赵焕霞

在平时学习中,有些性质和方法,自己编成歌诀,有利于记忆和理解。

例如在一次函数中,系数k决定图象的方向。当k>0时,图象如图A所示,像是一道撇。当k<0时,图象如图B所示,像是一道捺;当截距b>0时,图象如图C所示,在原点的上方。当截距b<0时,图象如图D所示,在原点的下方。而当截距为零时,则一次函数变为正比例函数,如图E所示。

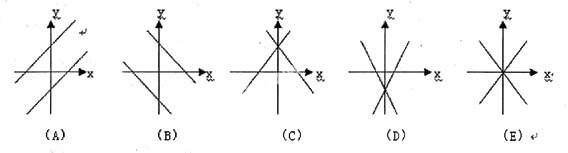
于是可编为:

“撇”k正,“捺”k负;

b的符号看截距:

上为正,下为负,

通过原点换函数。

又如在分解因式中,也可以用自编歌诀的办法,来理解因式分解的方法。

任何一道因式分解题,首先考虑的方法是提取公因式法;其次再考虑其他方法。如果是两项的,要考虑平方差与立方和、立方差公式;如果是三项的,就考虑完全平方公式与十字相乘法(即叉乘法);如果是四项、五项就要采用分组分解法;而如果前面的方法都不能分解时,则要采用拆项、添项的方法。另外,在分解因式时一定要分解到底。于是可编为:

提公因式第一法,

两项立方、平方差。

三项完全、叉乘式,

四项、五项分组法。

实在不行拆添项,

分解到底才不差。

再如在求不等式组的解集时,有如下特点:

1、当x>a,x>b且ab。(即两个都大时,取大的)

2、当x

3、当x>a,x

4、当xb且a

于是可编为:

大大大,小小小,

大小小大中间好,

大大小小解不了。

同学们在日常学习中,不妨也试着自己编一下,对加深记忆与理解还是有一定帮助的。

收稿日期:2009-03-30

作者地址:山东省诸城市辛兴小学262218