社会保障水平与产业结构调整的关系研究

2009-07-31杨贺王慧

商情 2009年9期

关键词：回归方程产值比重

杨　贺　王　慧

【摘要】本文主要研究中国产业结构调整对社会保障水平的影响，通过研究得出社会保障水平与产业结构间存在内在的联系的结论，因此，国家应加强社会保障制度建设。

【关键词】社会保障水平产业结构调整

CSI

一、研究假设

1.本文主要考虑产业结构调整对社会保障水平的影响。

2.社会保障的发展完全服从经济学分配理论中消费与积累的关系。

3.国家对社会保障制度的态度是理性的。

二、实证研究

在1978—1980年间，社会保障水平与产业结构调整之间的发展不相适应。这是由于社会保障水平虽有所发展，但第一产业的比重却有所增加，从而导致两者的CSI值为负数。在1980—1990年期间，第一产业的比重逐年下降，但社会保障水平的增长速度快于第一产业比重的下降速度，两者没有协调发展，使得CSI值大于1。在1990—1995年期间，第一产业的比重有了明显的下降趋势，但由于在此期间，我国社会保障支出水平也呈现下降的趋势，导致两者的CSI值小于0。从1995年至今，两者的CSI值大于0小于1，表明两者比较协调的发展。在此期间，第一产业的比重呈逐年下降的趋势，同时，社会保障支出水平呈逐年上升的趋势，但按照小口径统计的社会保障水平仍然远远低于社会保障水平的适度下限，说明我国的社会保障还没有为需要保障者提供充分的保障，还有发展的空间（见表2.1和表2.2）。

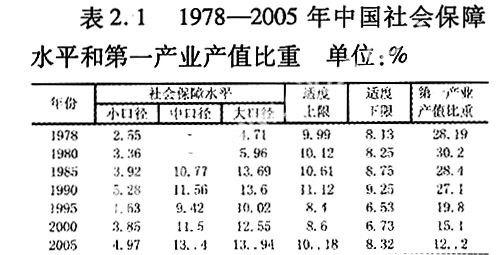
资料来源：1978—1990年社会保障水平数据、适度上、下限数据均源于穆怀中，《中国社会保障适度水平研究》，175；1995—2005年社会保障水平所需数据、老年人口比重均源于《中国统计年鉴2000》和《中国统计年鉴2005》，经计算而得；第一产业产值比重均源于《中国统计年鉴2006》。

资料来源：根据表2.1的数据计算而得

三、趋势预测

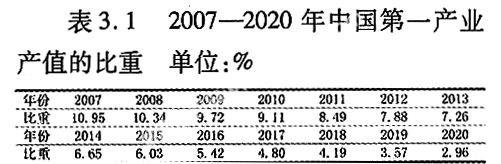
1．第一产业产值比重的趋势预测

预测所用数据的时间区间选择1999—2007年，预测内容为我国2008—2020年第一产业产值的比重。预测软件选择SPSS11.5。预测的假设：假设未来2008—2020年我国第一产业的发展趋势和1999—2007年的第一产业的发展趋势相同，而且这种趋势是线性的。得到下面的回归方程：

Y=-0.615X+16.486（R=0.968）

上面的方程的时间序列是以1999年为基期。把2008—2020年的时间序列数作为自变量代入回归方程，即可预测出2008—2020年我国第一产业产值的比重。

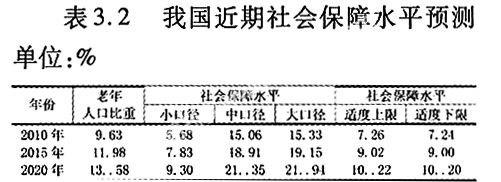
2．社会保障水平的趋势预测

预测所用数据的时间区间选择1997—2007年，预测内容为我国2010、2015、2020年的社会保障水平趋势预测。预测软件选择SPSS11.5。预测的假设：假设未来2008—2020年我国社会保障发展趋势和1997—2007年社会保障的发展趋势相同，而且这种趋势是线性的。得到下面的回归方程：按小口径统计：Y=-3.156+0.917X（R=0.774）按中口径统计：Y=-1.711+1.741X（R=0.870）按大口径统计：Y=0.676+1.522X（R=0.841）

把2010、2015、2020年的老年人口比重作为自变量代入回归方程，即可预测出这三年我国的社会保障水平。

3．我国近期CSI值的预测

根据上述预测的结果，可以计算出我国在2010、2015、2020年的CSI值（见表3..5）。在2020年之前，我国第一产业产值的比重会呈逐年下降的趋势，而社会保障水平则呈逐年上升的趋势，两者基本上能够协调发展。一般来说，按照小口径统计的社会保障水平低于适度下限，社会保障支出还有待提高，其发展落后于产业结构的调整。按照大、中口径统计的社会保障水平则明显高于适度上限，社会保障支出超度，其发展快于产业结构的调整。