Leibniz代数胚上动力系统的轨道范例与图示
2009-07-05王宝勤周小辉赵晓华袁丽霞
王宝勤,周小辉,赵晓华,袁丽霞
(1.新疆师范大学数理信息学院,新疆乌鲁木齐 830054; 2.浙江师范大学数理信息工程学院,浙江金华 321004)
Leibniz代数胚上动力系统的轨道范例与图示
王宝勤1,周小辉1,赵晓华2,袁丽霞1
(1.新疆师范大学数理信息学院,新疆乌鲁木齐 830054; 2.浙江师范大学数理信息工程学院,浙江金华 321004)
首先陈述Leibniz代数胚上的动力系统和在局部坐标系下该动力系统的方程,在此基础上,给出了动力系统轨道的范例和图示.
向量丛;Leibniz代数胚;动力系统的轨道
1 引言
人们曾把经典的Poisson括号和经典Hamilton系统推广为广义Poisson括号和广义Hamilton系统,正是这种推广使具有Hamilton形式的动力系统具有了很多特殊的动力学性质,但是这种推广系统和括号,只能描述保守力学系统,对耗散系统等是不能用Poisson括号描述的.由于许多领域不断提出的实际问题和众多学科发展的需要,很有必要对前述理论做进一步的推广[12].过去二十年来,学者们对这种推广的努力不断在进行,特别值得一提的是,推广系统的思想和方法相似于过去对广义Hamilton系统的做法,即用一个括号结构,但括号结构不是Poisson括号,而是Leibniz括号,Leibniz系统就是适合于某些耗散系统的动力学模型,还有许多重要的系统都能用Leibniz括号定义[3](如梯度系统和非完整约束简单力学系统等).这种推广的思想和趋势还在不断发展和深入,涉及到相应的几何描述层次也在提高,如所讨论的动力系统涉及丛结构,李代数胚和Leibniz代数胚等[45],为了更好理解和深入研究这些动力系统,我们在陈述理论的基础上给出了范例和轨道的图示.
2 Leibniz代数胚上的动力系统

赋予一个Leibniz代数胚结构的向量丛π1:B→M叫做M上的Leibniz代数胚,并记作(B,[·,·],ρ1,ρ2).
如果Leibniz代数胚的括号[·,·]是反称的(这种情形有ρ1=ρ2),它就叫做准李代数胚(Pre-Lie algebroid).而若Leibniz代数胚的括号[·,·]是对称的,它就叫做对称代数胚(这种情形有ρ1=−ρ2).
对于一个给定的σ∈P,用下边的关系式定义对偶丛空间B∗上一个函数FB∗σ
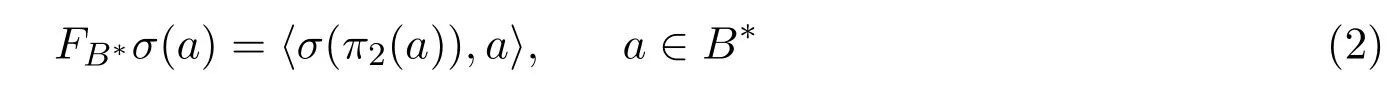
其中〈·,·〉是丛空间B和对偶丛空间之间的标准配对.
令Λ0是B∗上一个2-逆变张量场,并对任意两个函数f,g∈C∞(B∗)定义括号[·,·]Λ0为

如果对P中每一对截面(σ1.σ2),定义在B∗上的函数Λ0(dFB∗σ1,dFB∗σ2)是线性的,我们就说Λ0是线性的.
引理[4]对于每一个具有括号[·,·]和锚映射ρ1,ρ2的向量丛π1:B→M上的Leibniz代数胚结构,存在一个唯一的B∗上的2-逆变张量场Λ0,使得下述关系式成立

对所有σ,σ1,σ2∈P和f∈C∞(M).
反之,每一个B∗上的2-逆变线性张量场Λ0,用关系式(4),(5)定义一个B上的Leibniz代数胚.这个引理表明:在向量丛π1:B→M上的Leibniz代数胚结构和对偶向量丛π2:B∗→M的丛流形B∗上的2-逆变张量场之间建立起对应.
设dim M=n,dim B=m,{xi},i=1,···,n是M上的一个局部坐标系;再设{ej},j= 1,···,m是B的局部截面的一个基,而{ej},j=1,···,m表示B∗的局部截面对偶基;(xi,ya)和(xi,ξa)依次分别表示B和B∗上的坐标系.
易知,每一个B∗上的线性2-逆变张量场Λ0有如下形式
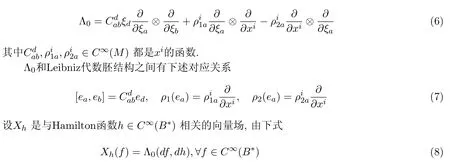
给出的相伴于向量场Xh的动力系统,叫做Leibniz代数胚π1:B→M上的动力系统.

3 范例和轨道图示
设向量丛π1:B=R3×R3→R3,其对偶丛π2:B∗=R3×(R3)∗→R3.
下边对每一个例子的叙述步骤是:
(1)先给出对偶丛B∗上的2-逆变线性张量场Λ,两个锚映射ρ1,ρ2的三阶方阵表示以及函数h的表达式.
(2)根据已知的Λ,ρ1,ρ2,h,写出相伴于Leibniz代数胚(R3×R3,Λ,ρ1,ρ2)的动力系统方程(9)和(10)的具体表达式.
(3)在一定条件下,给出动力系统在坐标系Ox1x2x3和Oξ1ξ2ξ3中的轨道图示.

取sinξ2=0.5,sinξ3=0.8;初值x1(0)=0.5,x2(0)=0.5,x3(0)=0.5
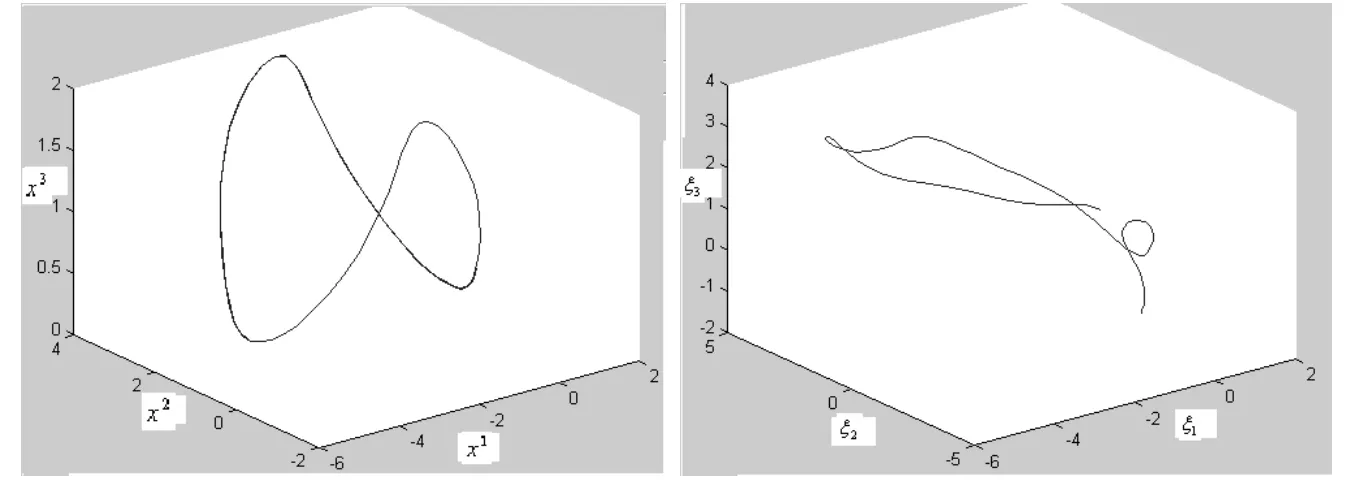
图1 例1的轨道图示图


图2 例2的轨道图示


n=2,5时的两组图如下:

图3 例3的轨道图示1

n=7,8时的两组图如下:
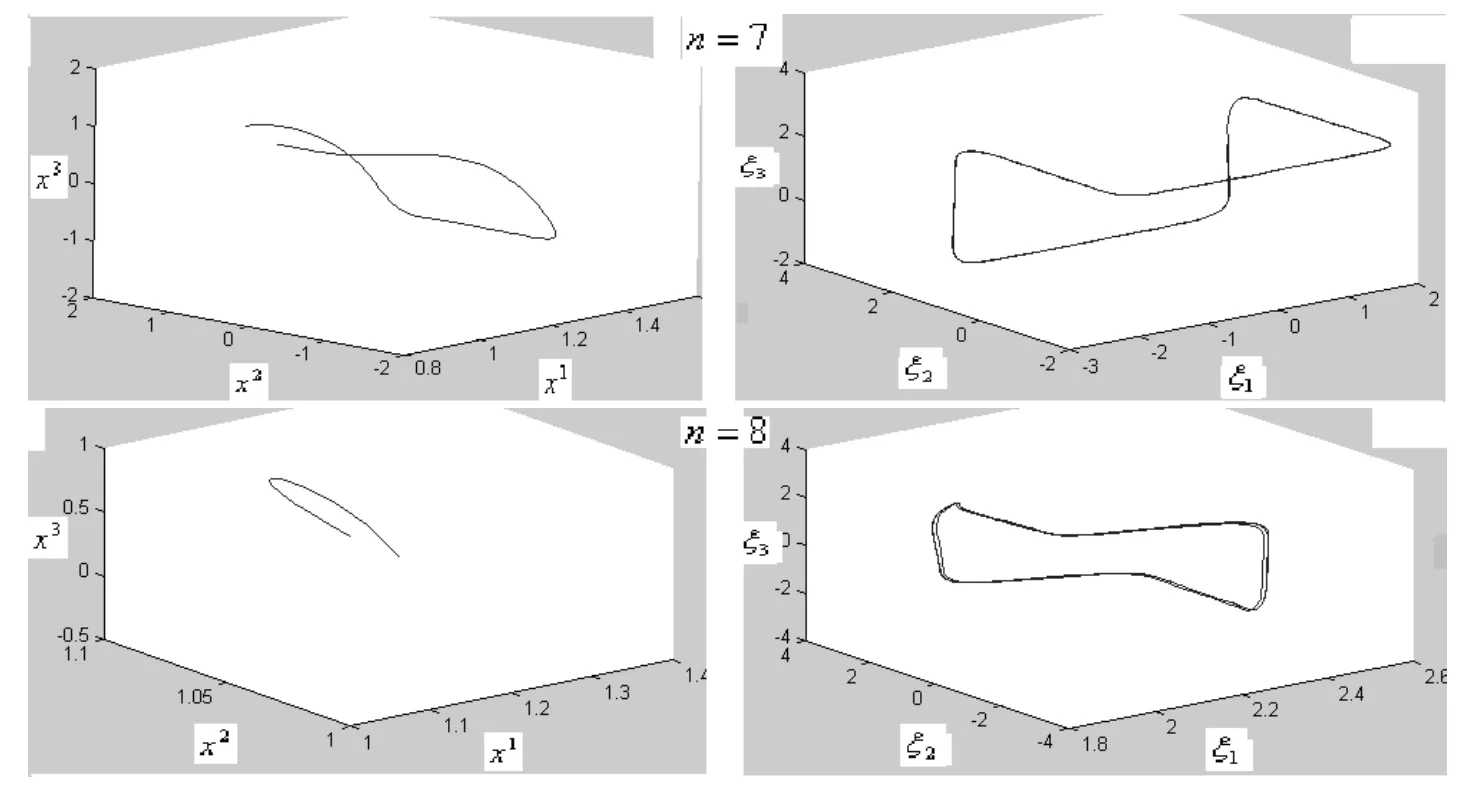
图4 例3的轨道图示2
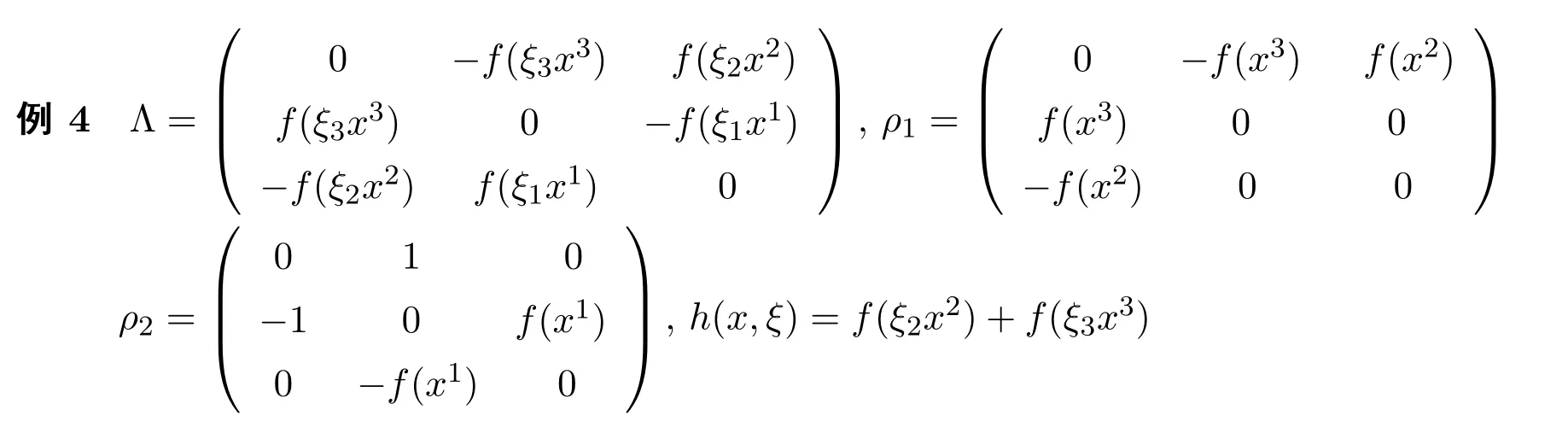

图5 例4的轨道图示
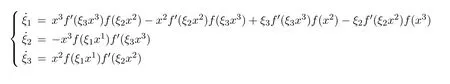

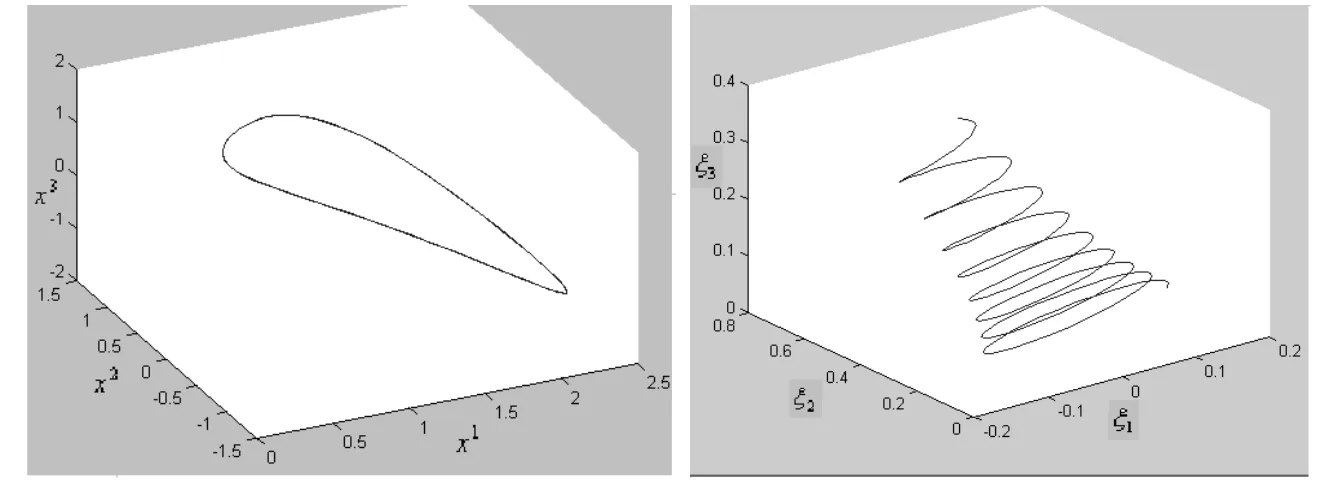
图6 例5的轨道图示
[1]王宝勤,袁丽霞,赵晓华.关于李群胚和泊松作用的讨论[J].纯粹数学与应用数学,2007,(23)4:487-492.
[2]袁丽霞,王宝勤.相配群胚上的诱导联络[J].数学进展,2008(5):617-624.
[3]王宝勤,张福娥,赵晓华.关于L流形的一些讨论[J].数学进展,2009(3):359-366.
[4]Grabowski J,Urbanski P.Lie algebroids and Poisson-Nijenhuis structures[J].Rep.Math.Phys.,1997,40:195-208.
[5]Ortega J P,Planas-Bielsa V.Dynamics on Leibniz manifolds[J].Journal of Geometry and Physics,2004,52:1-27.
Example and graphical representation of orbits of dynamical systems on Leibniz algebroids
WANG Bao-qin1,ZHOU Xiao-hui1,ZHAO Xiao-hua2, YUAN Li-xia1
(1.School of Maths-Physics and Information Science,Xinjiang Normal University,Urmuqi830054,China; 2.School of Maths-Physics,Information and Engineering Science,Zhejiang Normal University, Jinhua321004,China)
First of all,we explain dynamical systems on Leibniz algebroids and equations of this dynamical systems in a system of local coordinates.On the base of this,example and graphical representation of orbits of dynamical system are given.
vector bundle,Leibniz algebroid,orbit of the dynamical system
O186.1
A
1008-5513(2009)04-0642-07
2008-11-10.
国家自然科学基金(10872183),新疆师范大学优秀青年教师科研启动基金(XJNU0728).
王宝勤(1937-),教授,研究方向:现代微分几何及其应用.
2000MSC:53C12
