两种神奇的拓扑图形
2009-06-19潘楷林
潘楷林
拓扑学是19世纪发展起来的一个重要的几何分支。早在欧拉或更早的时代,就已有拓扑学的萌芽,那时候发现的个别问题,例如哥尼斯堡七桥问题、多面体的欧拉定理、四色问题等,都是拓扑学发展史上的重要问题,后来在拓扑学的形成中占着重要的地位。拓扑所研究的是几何图形的一些性质,它们在图形被弯曲、拉大、缩小或任意的变形下保持不变,只要在变形过程中不使原来不同的点重合为同一个点,又不产生新点,换句话说,这种变换的条件是:在原来图形的点与变换了图形的点之间存在着一一对应的关系,并且邻近的点还是邻近
 的点,这样的变换叫做拓扑变换。拓扑有一个形象的说法——橡皮几何学:因为如果图形都是用橡皮做成的,就能把许多图形进行拓扑变换。例如一个橡皮圈能变形成一个圆圈或一个方圈,但是一个橡皮圈不能由拓扑变换成为一个阿拉伯数字8,因为不把圈上的两个点重合在一起,圈就不会变成8。拓扑学专家创造出了许许多多迷人的物体。今天我们就来认识两种神奇的拓扑图形——莫比乌斯带和克莱因瓶。
的点,这样的变换叫做拓扑变换。拓扑有一个形象的说法——橡皮几何学:因为如果图形都是用橡皮做成的,就能把许多图形进行拓扑变换。例如一个橡皮圈能变形成一个圆圈或一个方圈,但是一个橡皮圈不能由拓扑变换成为一个阿拉伯数字8,因为不把圈上的两个点重合在一起,圈就不会变成8。拓扑学专家创造出了许许多多迷人的物体。今天我们就来认识两种神奇的拓扑图形——莫比乌斯带和克莱因瓶。
“莫比乌斯带”
数学上流传着这样一个故事:有人曾提出,先用一张长方形的纸条,首尾相粘,做成一介纸圈,然后只允许用一种颜色,在纸圈上的一面涂抹,最后把整个纸圈全部抹成一种颜色,不留下任何空白。这个纸圈应该怎样粘?如果是纸条的首尾相粘做成的纸圈有两个面,势必要涂完一个面再重新涂另一个面,不符合涂抹的要求,能不能做成只有一个面、一条封闭曲线做边界的纸圈儿呢?
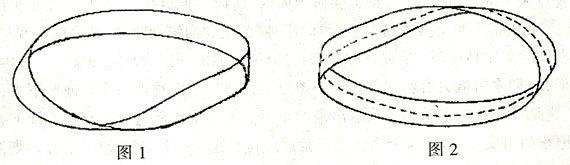
曾作过著名数学家高斯助教的莫比乌斯(Mobius,1790—1868),在1858年与另一位数学家各自独立发现了单侧的曲面,其中最闻名的是“莫比乌斯带”。如果想制作这种曲面,只要取一片长方纸条,把一个短边扭转180°,然后把这边跟对边粘贴起来,这样就形成了一条“莫比乌斯带”(如图1所示)。这样的纸带已不再具有两面,它只有单面。设想一只蜘蛛开始沿着莫比乌斯带爬,那么它能够爬遍整条带子而无须跨越带的边缘。要证实这一点,只要拿一支铅笔,笔不离纸连续地画线。那么,你将会经过整条的带子,并返回你原先的起点。
莫比乌斯带的另一个有趣的性质,只要你沿着如图2所示的带子中央的虚线剪开,把这个圈一分为二,照理应得到两个圈儿,奇怪的是,剪开后竟然是一个大圈儿。如果在纸条上画两条线,把纸条三等分,再粘成“莫比乌斯圈”用剪刀沿画线剪开,剪刀绕两个圈竟然又回到原出发点。猜一猜,剪开后的结果是什么,是一个大圈,还是三个圈儿?都不是。它究竟是什么呢?同学们自己动手做这个实验就知遭了。你就会惊奇地发现,纸带不仅没有一分为二,反而剪出一个两倍长的纸圈。有趣的是:新得到的这个较长的纸圈,本身却是一个双侧曲面,它的两条边界自身虽不打结,但却相互套在一起。我们可以把上述纸圈,再一次沿中线剪开,这回可真的一分为二了!得到的是两条互相套着的纸圈,而原先的两条边界,则分别包含于两条纸圈之中,只是每条纸圈本身并不打结罢了。
“莫比乌斯带”有点神秘,一时又派不上用场,但是人们还是根据它的特性编出了一些故事。据说有一个小偷偷了一位很老实农民的东西,并被当场捕获,将小偷送到县衙,县官发现小偷正是自己的儿子。于是在一
 张纸条的正面写上:小偷应当放掉,而在纸的反面写了:农民应当关押。县官将纸条交给执事官由他去办理。聪明的执事官将纸条扭了个弯,用手指将两端捏在一起,然后向大家宣布:根据县太爷的命令放掉农民,关押小偷。县官听了大怒,责问执事官。执事官将纸条捏在手上给县官看,从“应当”二字读起,确实没错。仔细观看字迹,也没有涂改,县官不知其中奥秘,只好自认倒霉。
张纸条的正面写上:小偷应当放掉,而在纸的反面写了:农民应当关押。县官将纸条交给执事官由他去办理。聪明的执事官将纸条扭了个弯,用手指将两端捏在一起,然后向大家宣布:根据县太爷的命令放掉农民,关押小偷。县官听了大怒,责问执事官。执事官将纸条捏在手上给县官看,从“应当”二字读起,确实没错。仔细观看字迹,也没有涂改,县官不知其中奥秘,只好自认倒霉。
县官知道执事官在纸条上做了手脚,怀恨在心,伺机报复。一日,又拿了一张纸条,要执事官一笔将正反两面涂黑,否则就要将其拘役。执事官不慌不忙地把纸条扭了一下,粘住两端。提笔在纸环上一画,又拆开两端,只见纸条正反面均涂上黑色。县官的毒计又落空了。
现实中可能根本不会发生这样的故事,但是这个故事却很好地反映出“莫比乌斯带”的特点。
“莫比乌斯带”在生活和生产中已经有了一些用途。例如,用皮带传送的动力机械的皮带就可以做成“莫比乌斯带”状,这样皮带就不会只磨损一面了。一种从莫比乌斯带得到灵感的针式打印机色带能使用更长的时间——因为可以更好的利用整个带子。如果把录音机的磁带做成“莫比乌斯带”状,就不会存在正反两面的问题,磁带就只有一个面了。在世界特殊奥林匹克运动史上,莫比乌斯环也有着特殊的意义,它象征着连接起全世界智障人士的友谊,彰显出特奥会所崇尚的“转换一种生命方式,您将获得无限发展”的理念。以2007年世界夏季特奥会会标“眼神”为主题的纪念雕塑,其采用的就是象征着无限发展的莫比乌斯环。瑞典1982年发行的《不可能的图形》邮票,图案是一个古里古怪的图形,如果你用指尖沿着这个古怪的图形上任何一个面顺着一个方向画下去,结果会发现,这是一个在现实中不可能造出来的东西。但如果你就这样一直顺着画下去。又会回到原来的出发点,似乎这个物体又不荒谬。其实这是一个立体化的“莫比乌斯圈”。发行这枚“不可能的图形”邮票,意在引导人们关注科学,探索宇宙不解之谜。
“克莱因瓶”
莫比乌斯带很神奇,但是,莫比乌斯带具有一条非常明显的边界。这似乎是一种美中不足。公元1882年,另一位德国数学家费力克斯·克莱茵(Felix Klein,1849—1925),终于找到了一种自我封闭而没有明显边界的模型,以他的名字命名的著名“瓶子”——“克莱因瓶”(如图3所示)。这种怪瓶实际上可以看作是由一对莫比乌斯圈沿边界粘合而成。如果把一个克莱因瓶适当地剪开来,我们就能得到两条莫比乌斯带。
这是一个像球面那样封闭的(也就是说没有边)曲面,但是它却只有一个面。在数学领域中,克莱因瓶是
 指一种无定向性的平面,比如二维平面,就没有“内部”和“外部”之分。“克莱因瓶”这个名字的翻译其实是有些错误的,因为最初用德语命名的时候名字中“Flache”是表面的意思,大概是误写为“Flasche”,这个词才是瓶子的意思。不过不要紧,“瓶子”这个词用起来也非常合适。在图片上我们看到,克莱因瓶的确就像是一个瓶子。它的结构非常简单,只是没有瓶底,它的瓶颈被拉长,然后似乎是穿过了瓶壁,最后瓶颈和瓶底圈连在了一起。如果瓶颈不穿过瓶壁而从另一边和瓶底圈相连的话,我们就会得到一个轮胎面。
指一种无定向性的平面,比如二维平面,就没有“内部”和“外部”之分。“克莱因瓶”这个名字的翻译其实是有些错误的,因为最初用德语命名的时候名字中“Flache”是表面的意思,大概是误写为“Flasche”,这个词才是瓶子的意思。不过不要紧,“瓶子”这个词用起来也非常合适。在图片上我们看到,克莱因瓶的确就像是一个瓶子。它的结构非常简单,只是没有瓶底,它的瓶颈被拉长,然后似乎是穿过了瓶壁,最后瓶颈和瓶底圈连在了一起。如果瓶颈不穿过瓶壁而从另一边和瓶底圈相连的话,我们就会得到一个轮胎面。
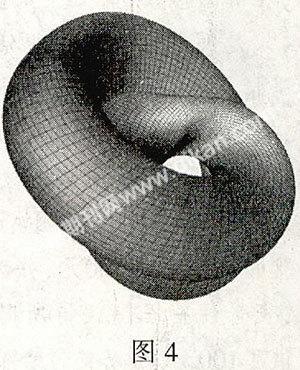
我们可以说一个球有两个面——外面和内面,如果一只蚂蚁在一个球的外表面上爬行,那么如果它不在球面上咬一个洞,就无法爬到内表面上去。轮胎面也是一样,有内外表面之分。但是克莱因瓶却不同,我们很容易想象,一只爬在“瓶外”的蚂蚁,可以轻松地通过瓶颈而爬到“瓶内”去——事实上,克莱因瓶并无内外之分。如果我们观察克莱因瓶的图片,有一点似乎令人困惑——克莱因瓶的瓶颈和瓶身是相交的,换句话说,瓶颈上的某些点和瓶壁上的某些点占据了三维空间中的同一个位置。但是事实并非如此。克莱因瓶是一个在四维空间中才可能真正表现出来的,曲面,如果我们一定要把它表现在我们生活的三维空间中。只好把它表现得似乎是自己和自己相交一样。也就是说,克莱因瓶的瓶颈是穿过了第四维空间再和瓶底圈连起来的,并不穿过瓶壁。如果我们把两条莫比乌斯带沿着它们唯一的边粘合起来,就会得到一个克莱因瓶(当然,我们必须在四维空间中才能真正有可能完成这个黏合,否则的话就不得不把纸撕破一点)。同样地。如果把一个克莱因瓶适当地剪开来,我们就能得到两条莫比乌斯带。除了我们上面看到的克莱因瓶的模样,还有一种不太为人所知的“8”字形克莱因瓶(如图4所示)。它看起来和上面的曲面完全不同,但是在四维空间中。它们其实就是同一个曲面——克莱因瓶。
克莱因瓶和莫比乌斯带一样,都是不可定向的。但是与之不同的是。克莱因瓶是一个闭合的曲面,也就是说它没有边界。莫比乌斯带可以嵌入到三维或更高维的欧几里德空间,而克莱因瓶只能嵌入到四维或更高维。空间。
