从几道习题看初中数学应用题的解法

杨立春

数学的应用题，无论对于小学生，还是对于初中生和高中生，多少年来都是他们学习的难点，如何才能正确地解答应用题呢?下面就通过几道习题的做法谈一谈我对于如何解应用题的几点看法。

例1：小明家想用34米长的篱笆，一面靠墙，围成一个面积是144平方米的鸡场，(1)若在墙上留2米宽的门，鸡场的长和宽各是多少米?(2)若在篱笆上留2两米宽的门，鸡场的长和宽各是多少米?

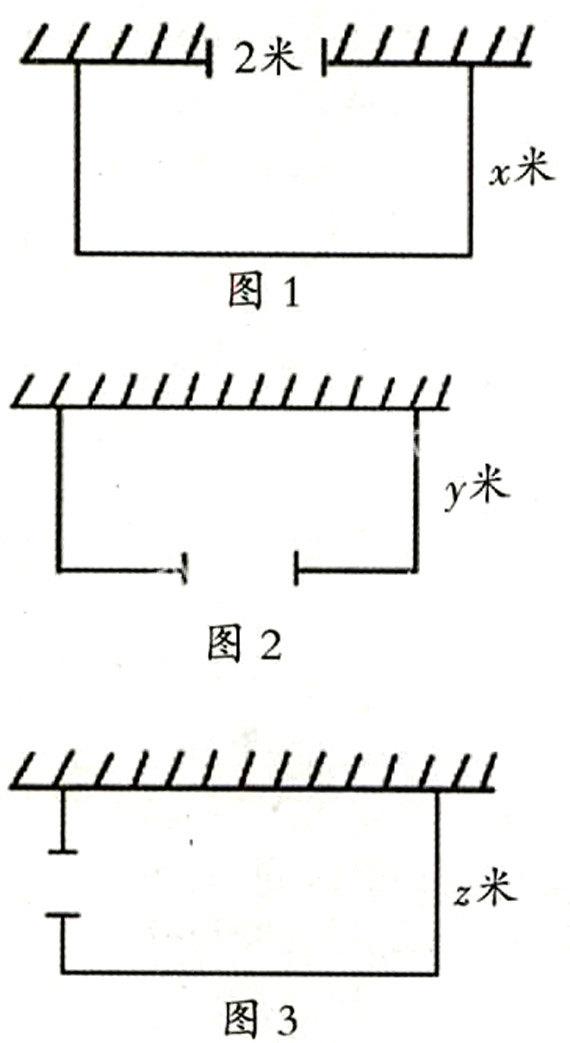
这道题的第一问较简单，在这一问中，门是留在墙上的，与篱笆的长度无关，如图1，设与墙垂直的篱笆长x米，则与墙平行的篱笆长为(34-2x)米，由方程x(34-2x)=144，得x1=8，x2=9，所以这个鸡场的长是18米，宽是8米，或长是16米，宽是9米。

这道题的第二问，正因为2米宽的门是留在篱笆上的，有很多学生的解题思路就被这道无形的“门”给挡住了，从而出现了很多的错误，在解答这一问时，考虑问题要全面，应该分两种情况去分析。

正确的解法是：当门留在与墙平行的篱笆上时，设与墙垂直的篱笆长是y米，则与墙平行的篱笆长是：(34-2y+2)米，由方程y(36-2r)=144，解得y1=6，y2=12，所以当2米宽的门留在与墙平行的篱笆上时，鸡场的长是24米，宽是6米或长和宽都是12米。

当门留在与墙垂直的篱笆上时，如图3，设与墙垂直的篱笆长是z米，则与墙平行的篱笆长是(34-2z+2)米，由方程z(36-2z)=144，解得：x1=6，x2=12，所以当2米宽的门留在与墙垂直的篱笆上时，鸡场的长是24米，宽是6米或长和宽都是12米。

例2：有一个长方形的猪舍，它的一边靠着长为14米的墙，其他三个边用35米长的铁丝网围成，甲同学的设计方案是长比宽多5米，乙同学的设计方案是长比宽多2米，问哪位同学的设计方案是可行的?

这道习题的解题思路是分别按照甲乙两名同学的设计方案求出长方形猪舍的长和宽，把不合实际的方案舍去就可以了。

甲同学的设计方案是长比宽多5米，若设猪舍的宽是。米，则猪舍的长是(a+5)米，根据两个宽与一个长的和是35米，可列出方程：2a+a+5=35，通过解方程得：d=-10，则a+5=15，由此可知，猪舍的长是15米，宽是10米，但原题中的墙是14米。墙体是不够长的，所以甲同学的设计方案不合实际，应该舍去。

乙同学的设计方案是长比宽多2米，若设猪舍的宽是^米，则猪舍的长应该是(b+2)米，因为两个宽和一个长的和是35米，可以列出方程：2b+b+2=35，通过解方程得b=11，则b+2=13，所以猪舍的长是13米，宽是11米，在这一方案中猪舍的长是13米，墙体的长是14米，墙体是够长的，所以在这个题目中乙同学的设计方案长比宽多2米，才是可行的。

例3：甲乙两个班级共有95名学生，现在从甲班调1人到乙班，甲班的人数就是乙班人数的90％，求甲乙两个班级的人数各是多少人?

在解这个题目时，设甲班有m人，则乙班有(95-m)人，根据题意可列出方程：m-1=(95-m+1)×90％，通过解方程得：m=46，则95-m=49，所以，甲班的人数是46人，乙班的人数是49人，学生在做这道题的时候，出现错误最多的是：把方程列成m-1=(95-m)×90％，正因为这个方程的解不是整数，从而认为这个题无解，经认真分析，学生之所以把这个题的方程列错，原因是他们只知道从甲班的m人中调出1人，是(m-1)人，而乙班的(95-m)人却没有变化，甲班调出的那个人到哪里去了呢，难道会蒸发吗?

通过这几道习题的解答，可以看出，解答数学应用题应从以下几个方面动脑分析：

1认真审题，多读几遍题，把题中的数量关系分析清楚，例如在解第一个题目的第二问时，设与墙垂直的篱笆长是y米时，与墙平行的篱笆长是(34-2y+2)米，而不是(34-2y)米，不要把2米宽的门给忽略了。

2考虑问题要全面，不能顾此失彼，尽管在第一个题目的第二问中两种情况的鸡场的长和宽一样，但这两种情况必须都要考虑到，在第三个题目中，既要考虑到从甲班的m人，调出1人是(m-1)人，又要同时考虑到，甲班调出的1人是调到乙班去了，乙班(95-m)人就必须增加1人，即乙班的人数是(95-m+1)人，如果只考虑甲班减1人。不考虑乙班加一人，自然想把题解对，是不可能的，另外还要记住，在解和一元二次方程有关的问题时，要考虑方程的判别式必须大于零，或等于零。

3有些题目要画出相应的图形，因为从第一个题目的图形可以看出，画图更能直观地体现出题中数量关系，如果不画图光凭想象容易把题中的条件漏掉而出现错误。

4列方程就是找出题中相等关系，在第一个题目中鸡场的面积是144平方米是相等关系，把这种相等关系用代数式表示即列出了方程，也就是说找相等关系对于列方程是最重要的。

5解应用题必须与生活实际相结合，求长度，速度不能出现负值，求人数不能出现小数，与生活实际、与题意矛盾或不相符的应该舍去，例如，在第二个题目中，给出墙的长是14米，当猪舍的长是15米时，墙就不够长了，所以应该把猪舍长15米，宽10米这种情形舍去。

6运用知识要灵活，不能教条，要以点代面、触类旁通，通过这几个习题的解题过程的分析，教师向学生讲解这一类问题的解题思路，能够提高学生分析问题和解决应用题的能力。

7有些应用题，相关的概念、含义、定义不能混淆，例如在有些经济问题中，进价、标价、售价、利润、利润率等不能混淆，标价不一定就是售价，售价减去成本才是利润，求利润率的计算方法是：利润率=(利润÷成本)×100％，求利润和利润率都与进价有关，如果这些量混为一谈，想把题解对是不可能的。

8解应用题要注意解题格式的书写。无论是设还是答，都不要忘记写单位，更不要把单位写错，在解题过程中用到的各个量的来龙去脉必须要交代清楚，例如在第一个题目中，方程：y=(36+2y)=144中的“36+27”实际上是由34-2y+2=36-2y计算得来的，如果不交代清楚，别人就会出现误解，光自己懂了还不行，必须让评卷入和看题者懂才可以。

综上所述，如果我们在解初中数学应用题的时候，能够综合的考虑到以上几个方面，就能够尽可能多的避免在解题时出现这样或那样的错误或漏洞，为正确的解决初中数学应用题打下坚实的基础。

编辑张烨