飞翼式飞行器结构布局与构件尺寸的两级优化

张仲桢　余雄庆　胡添元

文章编号：1006-0871(2009)01-0027-04

摘 要：为优化飞翼式飞行器的结构，提出同时考虑结构布局优化和构件尺寸优化的两级优化方法. 第1级优化将翼梁数量范围和位置范围作为约束，以重量最轻为优化目标，采用iSIGHT的多岛遗传算法优化结构布局；第2级优化给予第1级给定的结构布局方案，在满足应力约束和位移约束的前提下，确定各构件最佳尺寸，使该结构布局方案的结构重量最轻. 在第2级优化中，根据CAD外形模型和固定的结构布局参数，采用MSC Patran的PCL语言自动生成飞机的结构有限元模型，采用MSC Nastran优化全机结构，并将优化结果返回给第1级. 再通过两级之间的迭代获得结构布局和构件尺寸的最优设计方案. 整个两级优化过程用iSIGHT集成. 实例表明该方法为飞翼式飞行器结构布局和构件尺寸协同优化问题提供1种有效的解决办法.

关键词：飞翼；结构布局；结构尺寸；两级优化；MSC Patran；MSC Nastran；iSIGHT

中图分类号：V214.19；TB115

文献标志码：A

收稿日期：2008-06-02 修回日期：2008-07-07

Two-level optimization on structural layout and component size of flying wing aircraft

ZHANG Zhongzhen，YU Xiongqing，HU Tianyuan

(National Defense Key Lab. of Fundamental Sci. for Advanced Design Tech. of

Flight Vehicle，Nanjing Univ. of Aeronautics & Astronautics，Nanjing 210016，China)

Abstract：To optimize the structure of flying wing aircraft，a tow-level optimization method is proposed considering the optimization of structural layout and component size at the same time. In the first level，the number and position of wing beam are taken as the constraint，the lightest weight is taken as the optimization object，and the structural layout is optimized by multi-island genetic algorithm of iSIGHT. The second level is based on the structural layout obtained by the first level，the best size of every component is confirmed while the constraint of stress and displacement is satisfied，and so the lightest structure is obtained. In second level，according to the profile model of CAD and the fixed parameters of the structural layout，the finite element mode of an aircraft model is automatically generated using PCL of MSC Patran，the structural size of the whole aircraft is optimized using MSC Nastran，and the optimization results are returned to the first level. The optimal optimization deign solution of the structural layout and component size is achieved by the iteration between the first level and the second level. The optimization of the two levels are integrated by iSIGHT. The examples indicate that the method provides an effective solution for the collaborative optimization of structural layout and component size for flying wing aircraft.

Key words：flying wing；structural layout；structural size；two-level optimization；MSC Patran；MSC Nastran；iSIGHT

0 引 言

飞机结构的初步设计包含2个方面[1]：(1)确定结构布局；(2)确定每个结构件的尺寸.结构初步设计的任务是：在满足强度、刚度和工艺等要求的前提下，确定结构布局和结构件尺寸，并尽量使结构重量最轻[2，3].

优化方法有助于设计人员能获得更好的结构设计方案.目前大多数结构分析和优化软件(如MSC Nastran和ANSYS等)只能进行结构尺寸优化[4]，结构布局仍主要依靠设计人员的经验来布置.但对于新型飞机，以往的经验不一定能获得最优的结构布局和尺寸设计方案.更好的办法[5]是在飞机初步结构设计阶段，同时考虑结构布局优化和尺寸优化，从而得出最优结构设计方案.

针对飞翼外形飞行器结构初步设计问题，提出1种两级优化策略，即第1级对结构布置进行优化，第2级对结构件尺寸变量进行优化，以期获得最优结构设计方案.

1 优化问题描述

根据飞翼外形设计结果(见图1)，需完成结构件布置和确定各受力构件的尺寸，使结构重量尽量轻.全机所有结构材料均采用硬铝LY12，弹性模量为69 GPa，密度为2 700 kg/m3，泊松比0.3.按常规结构布局设计的经验，1种可能的布局形式见图2.

图 1 全机CAD外形

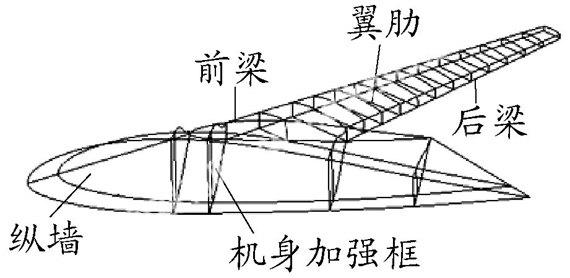
图 2 结构布局示意图

该机翼结构采用双梁式布局形式，前梁在弦长15%处，后梁在弦长65%处，肋距约为580 mm，共布置14根肋.但该布局方案不一定为最优方案，而采用布局和尺寸同时优化方法可能会获得更好的结构设计方案.

用优化设计方法描述这一结构布局和尺寸设计问题，可表达为目标：全机结构重量最轻.设计变量：X₁，X₂.设计约束：构件正应力≤450 MPa，构件剪应力≤250 MPa，最大位移≤5%半展长，翼梁个数取值为2或3，前梁位置范围在0.135～0.165，后梁位置范围在0.6～0.7.

其中：X₁为描述结构布局特征的设计变量，包括机翼梁的个数和位置；X₂为描述构件尺寸的设计变量，包括机身加强框厚度、上下蒙皮厚度、纵梁厚度、加强框缘条面积、支柱面积，机翼上下蒙皮厚度、翼肋厚度、梁腹板厚度、梁缘条面积、支柱面积、肋缘条面积.在飞翼结构布置设计中，采用多梁式布局，梁的个数取值范围为2或3.前梁和后梁位置变量范围分别在当地弦长的13.5%到16.5%之间和60%到70%之间.翼肋的作用是维持机翼剖面形状，提高蒙皮稳定性.本文不考虑稳定性约束，翼肋个数按经验确定为14，不作为设计变量.

在该优化问题中，设计变量包含结构布局参数和尺寸参数，设计变量类型包含连续设计变量和离散变量(翼梁个数)，用现有的CAE软件(如MSC Nastran)无法求解，必须探索新的优化策略.

2 优化策略与实施流程

2.1 两级优化策略

为了解决上述结构布局和尺寸同时优化问题，采用两级优化策略，即将优化过程分为结构布局优化和结构尺寸优化2个层次，结构布局优化和结构尺寸优化之间的关系见图3.

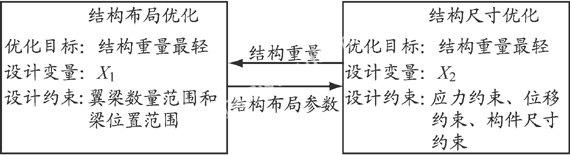
图 3 飞翼结构两级优化策略

结构尺寸优化(第2级)的任务是：对于第1级给定的结构布局方案，在满足应力约束和位移约束的前提下，寻找各构件最佳尺寸，使该结构布局方案的结构重量最轻.在第2级优化中，结构布局参数固定，采用MSC Nastran软件提供的优化方法[4]，对全机的结构尺寸进行优化，将优化结果(结构重量)返回给第1级.在第1级优化中，根据第2级优化的结果，寻找最佳结构布局方案(机翼梁的个数和位置)，使机翼结构重量最轻.由于第1级优化问题中的设计变量包含连续设计变量和离散变量，所以采用遗传算法对机翼和机身内部结构进行结构布局优化.通过第1级布局优化与第2级尺寸优化之间的多次迭代，最终获得结构布局和构件尺寸的最优设计方案.

2.2 优化过程的实现

实现上述飞翼结构两级优化策略流程见图4.

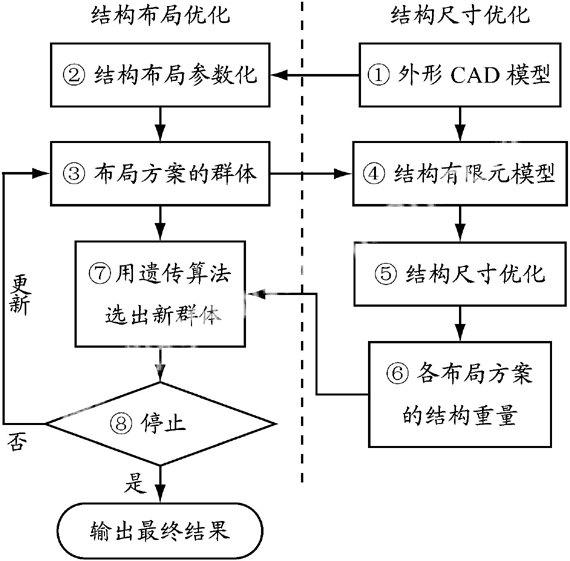
图 4 飞翼结构两级优化流程

综合应用iSIGHT软件[6]的集成和优化功能，以及MSC Patran和MSC Nastran软件[4]的结构分析和优化功能实现该流程各环节.具体实现过程如下：

(1)将图1所示的外形CAD模型以IGES格式导入MSC Patran环境.

(2)结构布局参数化：将机翼梁的个数和位置设置为描述飞翼结构布局参数.其中，机身加强框与机翼梁对接，所以机翼梁个数能确定机身加强框个数.翼肋沿机翼展向均匀布置14根.若机翼结构布局为三梁式，则中间梁布置在前后两梁中点，所以只需设定前梁和后梁位置2个变量.一旦这几个结构布局参数确定，整个飞翼结构布局就被确定.

(3)根据遗传算法生成结构布局参数的群体.采用iSIGHT软件中提供多岛遗传算法进行布局优化.多岛遗传算法需要设置3个参数：岛数、每个岛上的样本个数以及遗传代数.对于该优化问题，设置6个岛，每个岛5个样本，需要繁殖10代，所以在第1级优化中共需计算300次.

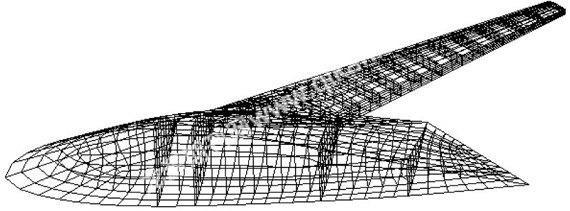
图 5 结构有限元模型

(4)根据结构布局参数和CAD外形模型，采用MSC Patran二次开发语言PCL自动生成飞机的结构有限元模型.[7]所生成的其中1个结构有限元模型见图5.模型的有限元网格采用四边形4节点等参面单元和2节点杆单元，边界约束为中间对称面处固支.根据气动计算出的升力分布，采用场力加载方法将载荷施加在全机蒙皮上，另外还考虑燃油卸载和自身结构重量.

(5)结构尺寸优化采用MSC Nastran软件中提供的序列二次规划法.[4]其中，杆单元以截面面积为优化变量，面单元则以厚度为优化变量.为了减少计算量，对机翼采用区域划分法对优化变量进行合并.把机翼沿展向划分为3个区域，每个区域上的优化变量有该区域中肋腹板的厚度、上蒙皮的厚度、下蒙皮的厚度、梁腹板的厚度、梁上缘条的截面面积、梁下缘条的截面面积、肋缘条的截面面积和支柱的截面面积共8个优化变量，加上机身设置的优化变量，整个结构的优化变量约为45个.

(6)当结构尺寸优化结束后，MSC Nastran将结果存放在*.f 06文件中.用iSIGHT提取*.f 06文件[4]的优化结果(即全机重量)，并将这些结果返回布局优化层次.

(7)在布局优化层次中，遗传算法对种群中每个个体的适应度进行评估，并通过交叉和变异等算子生成新的种群.

(8)返回第(3)步，更新种群，执行步骤(3)~(7)，直到规定的繁殖代数停止.最后提取最优结构布局参数和各构件尺寸参数，从而完成结构布局和尺寸优化任务.

图4所示流程中各环节在iSIGHT环境中集成，整个优化流程自动进行.在CPU为P4 3.2 GHz，内存3.5 GB的计算机上计算时间约为8.5 h.

3 优化结果

经过优化后最终获得的结构布局方案为3个梁，前梁位置为弦长16.22%处，布局方案后梁位置为弦长61.53%处，见图6.在优化过程中，结构重量的变化历程见图7，最终获得的结构重量为796.38 kg.

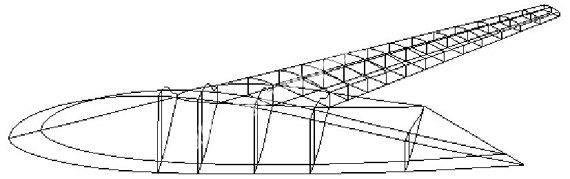
图 6 优化后的结构

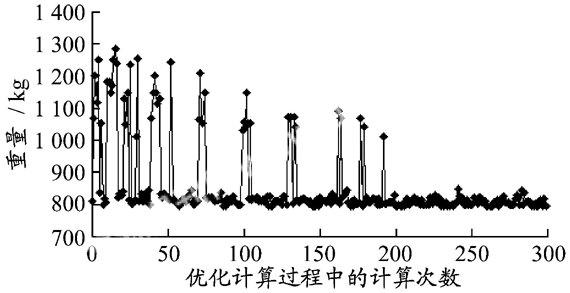
图 7 结构重量变化历程

按照传统经验的方案，获得的最轻结构重量为1 123.8 kg.因此，与原设计方案相比，采用两级优化方法所获得的结构设计方案，重量能减少29.14%.

优化后的结构布局增加1个梁和框，见图6.从最终尺寸优化结果看，机翼在增加1个梁和框的情况下结构重量反而减轻.这是因为增加的梁和框承担部分载荷，减少原先结构(前梁、后梁、蒙皮等)的受载，在同样应力和位移约束下，这些结构尺寸相应减小，综合效果是使得总的结构重量减轻.

4 结 论

针对飞翼式飞行器结构的布局和尺寸优化问题，提出1种两级优化策略，通过综合应用iSIGHT软件和MSC Patran/Nastran软件的功能实现这种两级优化策略.优化结果表明该两级优化策略和技术途径能有效解决飞翼式飞行器的结构布局和尺寸协同优化问题.进一步研究工作将考虑稳定性约束，将翼肋的个数作为设计变量，进行结构布局优化.该思路和方法也可以用于解决其他结构布局和尺寸优化问题.

参考文献：

[1] SENSMEIER M D，STEWART B T. Rapid generation and assessment of aircraft structural topologies for multidisciplinary optimization and weight estimation[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures，Struct Dynamics，& Mat Conf，USA：AIAA，2006.

[2] YOUNG J A，MCGILLIVARY S R. Full aircraft conceptual layout optimization techniques[C]//Proc 7th AIAA/NASA/USAF/ISSMO Symp on Multidisciplinary Anal & Optimization，USA：AIAA，1998.

[3] 黄国宁，陈海，霍应元. MSC Nastran优化功能在结构强度设计中的应用[J]. 计算机辅助工程，2006，15(S1)，50-52.

[4] 隋允康，杜家政，彭细荣. MSC Nastran有限元动力分析与优化设计使用教程[M]. 北京：科学出版社，2004：207-227.

[5] 王伟，杨伟，赵美英，等. 基于神经网络预杂交算法的机翼结构优化设计[J]. 机械设计，2007(8)：49-51.

[6] KOCH P N，EVANS J P，POWELL D. Interdigitation for effective design space exploration using iSIGHT[J]. J Struct & Multidisciplinary Optimization，2002，23(2)：111-126.

[7] NAWIJN M，van TOOREN M J L，BERENDS J J. Automated finite element analysis in a knowledge based engineering environment[C]// 44th AIAA Aerospace Sci Meeting & Exhibit，USA：AIAA，2006.

(编辑 廖粤新)