多媒体与数学教学

龚　萍

摘 要 多媒体技术和数学教学的学科特点结合起来，可以使教学的表现形式更加灵活和多样性，可以使原本枯燥的数学教学充满活力，可以使深奥难懂的概念变的浅显易懂

关键词 多媒体，数学教学

随着21世纪的到来，以计算机和互联网为代表的当代信息技术，正在以惊人的速度改变着人们的生存方式和学习方式，也迫切需要我们改变教育方式。多媒体辅助教学已成为现代化教育中的一种有效手段，恰当地使用多媒体教学，能利用图形、图像、文本、声音、动画等多种媒体信息刺激学生的感官，通过形象生动的画面、悦耳动听的音乐等充分展示知识的形成过程，培养学生的思维能力，提高学生的综合素质，从而全面提高教学质量。信息技术和数学教学的学科特点结合起来，可以使教学的表现形式更加形象化、多样化、视觉化，有利于充分揭示数学概念的形成与发展，数学思维的过程和实质，展示数学思维的形成过程，给教学带来了新的生命力，使数学课堂教学收到事半功倍的效果。本来枯燥无味的课堂因计算机的作用而使得本身抽象的知识变得生动活泼且易懂明了。

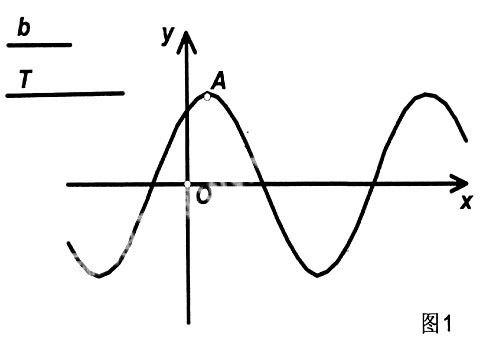
“函数”是中学数学中最基本、最重要的概念，它的概念和思维方法渗透在高中数学的各个部分；同时，函数是以运动变化的观点对现实世界数量关系的一种刻划，这又决定了它是对学生进行素质教育的重要材料。可以用《几何画板》根据函数的解析式快速作出函数的图象，并可以在同一个坐标系中作出多个函数的图象，如在同一个直角坐标系中作出函数y=x2、y=x3的图象，比较各图象的形状和位置，归纳函数的性质；还可以作出含有若干参数的函数图象，当参数变化时函数图象也相应地变化，如在讲函数y=Asin(ωx+φ)的图象时，传统教学只能将A、ω、φ代入有限个值，观察各种情况时的函数图象之间的关系；利用《几何画板》则可以以线段b、T的长度和A点到x轴的距离为参数作图（如图1），当拖动两条线段的某一端点（即改变两条线段的长度）时分别改变三角函数的首相和周期，拖动点A则改变其振幅 ，这样在教学时既快速灵活，又不失一般性。

在讲授平面向量知识时，我们可以在《平面向量的基本概念》及《平面向量的坐标表示》的教学中，利用Powerpoint制作动态的平面向量课件，学生通过探索，发现了平面向量的基本概念，深刻的理解了平面向量的坐标表示的意义和作用。

在讲解与《空间四边形》有关的问题时，如果只利用模型让学生观察，在黑板上作出空间四边形的平面直观图，大部分学生在课后解决相关的问题的时候，总自然而然的认为空间四边形两条对角线是相交的。我们可以在教学中利用三维立体几何画板导入基本图形，现场制作旋转运动的空间四边形图形，现场添加线条，在旋转运动过程中让学生感受空间立体图形的形象，培养学生的空间观察和思维能力，从而使他们在观察过程中留下空间四边形两条对角线不相交的深刻印象，在解决其它有关问题时不致出错，同时学生在这个过程中发现了异面直线的概念，为后面的《异面直线》的教学奠定了基础。

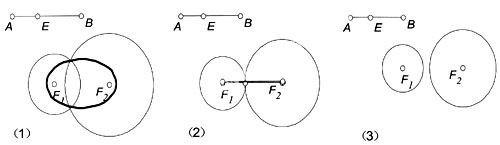
比如在讲椭圆的定义时，可以由“到两定点F1、F2的距离之和为定值的点的轨迹”入手——如下图，令线段AB的长为“定值”，在线段AB上取一点E，分别以F1为圆心、AE的长为半径和以F2为圆心、AE的长为半径作圆，则两圆的交点轨迹即满足要求。先让学生猜测这样的点的轨迹是什么图形，学生各抒己见之后，老师演示图（1），学生豁然开朗：“原来是椭圆”。这时老师用鼠标拖动点B（即改变线段AB的长），使得|AB|=|F1F2|，如图（2），满足条件的点的轨迹变成了一条线段F1F2，学生开始谨慎起来并认真思索,不难得出图（3）

（|AB|<|F1F2|时）的情形。经过这个过程，学生不仅能很深刻地掌握椭圆的概念，也锻炼了其思维的严密性。

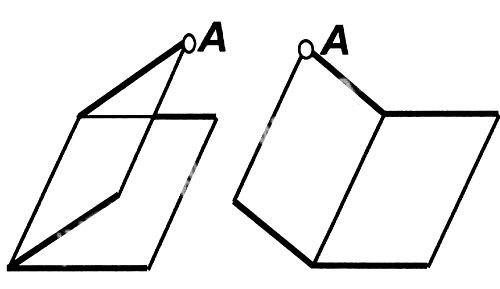
在讲二面角的定义时（如图），当拖动点A时，点A所在的半平面也随之转动，即改变二面角的大小，图形的直观地变动有利于帮助学生建立空间观念和空间想象力。

在讲授线性规划时，可以充分利用几何画板作图：先作出可行域，在作出初使直线，利用该直线的可移动性，让学生发现当直线经过可行域时，在何处可以使目标函数取得最值。原本只能画在黑板上的图象，需要借助教师通过移动直尺划过可行域，而学生理解的也很费劲。现在学生通过多媒体的演示，可以很轻松的理解线性规划问题了。

由此可见，运用多媒体教学，不但能充分刺激学生的感官，调动他们的积极性，并能激发学生创造性的学习，发展他们的思维，培养运用知识的综合能力。总之，利用多媒体辅助进行教学是教育改革实践中的一种新探索，不仅能调动学生的学习积极性，而且学生的数学知识、能力和思维等智力因素也得到发展。我们深信：教学改革伴随着多媒体手段的普遍运用，课堂教学效率将会不断提高，学生的整体素质将得到全面发展。