美元数独
2009-04-14孙维梓
科学大众(中学) 2009年3期
孙维梓
假定你已经对数独游戏有了一定的了解,但是当你见到图1中那样的图案时,你仍然会产生疑惑:难道这也算是数独?没错,它的确是一种新颖别致的数独,但是被设计成了美元的符号,也就是形如$那样,由一条直线和一条呈S状的曲线组成。直线与曲线上分别独有9个格子,你得填入数字,使得这两条线段上都能具有从1到9的全部数字,但是在任何两个相邻格里不准出现相邻的数字,如1与2,2与3等等。
那么如何着手解决呢?能保证答案是唯一的吗?这得动一番脑筋才行。
请看,在直线上已经有2,3,8,9四个数字,还缺少1,4,5,6,7这五个数。而曲线上有了2,5,7,8,9五个数字,还缺少1,3,4,6这四个数。注意到直线和曲线有两个公共格,而上列这两组缺少的数中间共有的却有1,4及6这样三个数。那么究竟哪两个数才是我们所需要填入到公共格里的呢?

看来最上面的公共格中由于耍避免出现相邻数,所以不能填4及6了,唯一能填的只有1!剩下那个中央公共格里,看起来4或6都能够填。可是你看:在曲线上还有三个空格,能填的数只有3,4及6这样三个数。由于3与4不能相邻,所以6必须写在3与4的中间,所以能填入中央公共格的只能是4,别无它法。这样曲线上的三个数就全解决了,如图2所示:

下面我们再来观察直线。它已经有了六个数,需要解决的是:5,6,7该怎么填。稍一思索,就能知道你必须把6写在最下一格,才能使5与7成为相邻的数。但是5不能与中央格的4相邻,所以在4的下面只能填7,而5则要写在7的下面。好,万事俱备啦!美元到手,请看图3:
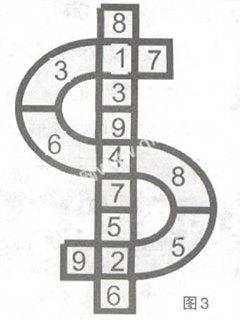
怎么样?美元数独挺有意思吧?那么请你自己来解答另外一道题如何?它就是图4:

美元数独的唯一答案如下:
