灰色关联度法在地下水脆弱性评价与分区中的应用

孙丰英，许光泉，唐文锋

（1. 安徽理工大学，淮南 232001；2. 淮南联合大学，淮南 232038）

灰色关联度法在地下水脆弱性评价与分区中的应用

孙丰英1，许光泉1，唐文锋2

（1. 安徽理工大学，淮南 232001；2. 淮南联合大学，淮南 232038）

采用灰色系统理论中的灰色关联度分析方法对地下水脆弱性进行研究，选取地下水位埋深、包气带岩性、含水层砂层厚度等6个因子建立了脆弱性评价指标体系，采用离差最大化方法确定评价指标的权重，使权重的分配有了一定的理论依据。并以MATLAB为平台编制了常用计算程序，应用于抚州市地下水脆弱性评价与分区，取得良好结果。

灰色关联度；地下水脆弱性；指标体系；离差最大化方法

0 引言

“脆弱性”是系统失稳后产生后果的严重性，是灾害形成的根源[1]。地下水脆弱性反映了地下水系统遭受污染的潜在可能性，污染物在不同的地下水系统中具有不同的迁移转化能力，目前缺乏这方面的系统研究。要有效控制地下水污染，必须研究不同地下水系统的脆弱性。

影响地下水脆弱性的潜在因素很多，要想建立一个包含所有影响因素的评价因子体系在实际应用中是不现实的[2]。首先因子越多，因子之间的关系也就越复杂，容易造成因子之间相互关联或包容（如含水层的水动力传导系数与含水层岩性密切相关）；其次，有些因子（如土壤成分、含水量、粘土矿物含量等）在区域性评价中取值比较困难，可操作性较差；另外因子太多，也会冲淡主因子的影响。

灰色系统理论提出的灰色关联分析，可在不完全的信息中对要分析研究的各因素，通过一定的数据处理，在随机的因素序列间，找出它们的关联性。因此，特别适合像地下水脆弱性这类数据有限、没有模型、复杂而且具有不确定性问题的分析和评价。灰色关联分析是一种多因素统计分析法，它以各子因素时间序列与母因素时间序列数据为基础计算母子因素的关联度，用关联度来描述母子因素间关系强弱、大小和次序[3]。

(1) 灰色关联度算法

制定一个参考数据：

x0(x0=(x0(1),x0(2), ... x0(n))),

有m个比较数据列：

x1,x2,...xm(xi=(xi(1),xi(2),...xi(n));i=1,2,...,m)。

按下式计算xi相对于x0在第j个元素上的关联系数[4](j=1,2,...,n)

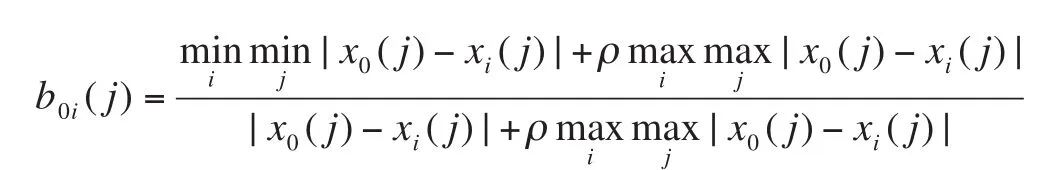
式中：ρ为分辨系数，其取值的大小可以控制对数据转化的影响，通常在(0,1)内取值。一般情况下取ρ=0.4，越小越能提高关联系数间的差异。

从上式关联系数计算得到的是各比较序列与参考序列在各点的关联系数值，结果较多，信息过于分散，不便于比较，因此，有必要将每一个比较数列各个时刻的关联系数集中体现在一个数值上，即灰色关联度。一般可采用求平均值或加权求和的方法[4]，求出xi对x0的关联度：

其中， 是比较序列与参考序列在第j个指标的权系数，利用离差最大化来计算[5]。

(2) 算法的MATLAB实现

为了计算方便，笔者以MATLAB为平台开发了无量纲化的Matlab程序、计算关联系数矩阵的Matlab程序以及离差最大化求权重等函数程序。因篇幅所限，仅给出离差最大化计算权重的Matlab程序。

1 灰色关联度应用于抚州市地下水脆弱性评价与分区

抚州市位于江西省东部，抚河中游。研究区地理坐标为东经116°15′ 116°22′，北纬27°57′28°01′。区内海拔标高40～60m，发育一、二、三级阶地，为第四系冲积层覆盖。一、二级阶地具有明显的双层结构，上部为0.5～2m厚的粉细砂层或耕作层，下部为4～6m厚的砂砾石层。三级阶地上部为4～9m厚的红粘土层，下部为少量砂砾石。

为了取得较准确的资料，针对区内地质地貌、工农业布局、水系及污染情况，在抚河、宜黄河流域的不同地段均衡取点，共布置20个地下水监测点。

（1）DITRQP评价模型

在进行指标选取时，遵循指标的稳定性、独立性、可比性和易操作性原则[6～8]。此次地下水脆弱性评价指标包括地下水埋深（D），包气带岩性（I），浅层地下水含水层砂层厚度（T），含水层的补给强度（R），地下水水质现状（Q）和污染源（P）等。

本文地下水脆弱性评价模型为经过修改的DRASTIC模型[9,10]：

DrDw+IrIw+TrTw+RrRw+QrQw+PrPw=DITRQP

式中：下标r为划分等级，Dr为r等级量化值，Dw为权重，DITRQP为评价综合指数。

地下水埋深、浅层含水层砂层厚度、地下水质量等与地下水脆弱性呈负相关性，值越大，评分越低；含水层的净补给、降水入渗系数与地下水脆弱性呈正相关性。以0.2作为等级划分间隔，将地下水资源脆弱性划分为五个等级，根据以上各评价指标与地下水脆弱性关系，进行如下量化分级（表1）。

表1 地下水脆弱性评价指标的量化值

（2）网格剖分与编号

进行网格剖分是将空间大区域划分为小的统计单元，以便于数据的获取和样本空间的统计。本文根据研究区面积和数据的精度，对研究区进行间距为0.1km×0.1km正方形网格剖分，剖分单元共计5980个（图1）。

图1 研究区网格剖分图

（3）评价结果

设k为研究样本的序号，即区内20个监测点。k0为各评价指标的最优值，作为标准参考数据列，即k0=[0.5；0.4；1.4；18.0；0.8；0.9]，利用上述方法进行灰色关联度计算，其原始数据及评价结果见表2。

表2 地下水脆弱性评价指标测点数据及评价结果

应用上述的离差最大化方法确定的各指标的权重w为：w =[0.167，0.146，0.170，0.193，0.186，0.137]，表明此6个评价指标对地下水脆弱性的影响程度为：含水层的净补给＞地下水质量＞含水层砂层厚度＞地下水埋深＞包气带岩性＞污染源。

由表2可以看出灰色关联度算法算得的结果跟运用RBF神经网络法计算的结果基本吻合，进一步说明了灰色关联度算法的可靠性。

最后将算得的DITRQP模型综合评价指数结果通过内插法分配到各评价单元[11,12]，利用MAPGIS的空间分析和编辑功能完成地下水脆弱性分区，如图2。

图2 地下水脆弱性评价分区示意图

高脆弱区大致分布在河流两岸和主城区一带，沿河两岸呈带状分布组成一、二级阶地，为松散岩类孔隙含水层，地下水位埋深较浅。一般脆弱区主要分布在区内的东北部、主城区边缘及抚北等地，本区具有明显的双层结构，地下水天然保护条件好。低脆弱区分布在南部及抚北部地区，人口稀疏，远离市区和工业区，污染物渗入地下的量较少，即使有污染因子，也由于地下水的不停交替与淡化作用，使其脆弱性程度相对最低。

2 结语

（1）选用灰色关联度方法进行地下水脆弱性评价与分区，使用的数据量较一般的函数相关性分析和回归分析的要求较少而分辨率高，回避了不同指标的数量集和量纲，具有很好的扩展性。

（2）利用灰色关联度方法进行研究，并与人工神经网络结果进行比较，结果基本一致。抚州市的应用实践表明：所得结果具有较好的客观性，是提高地下水脆弱性评价与分区客观度的一种有效途径。

[1] 商彦蕊，史培军等.人为因素在农业灾害形成过程中所起作用的探讨——以河北省旱灾脆弱性研究为例[J].自然灾害学报,1997(4):35～43.

[2] Vrba J, Zaporozec A. Guidebook on mapping groundwater vulnerability[M]. International Association of Hydrogeologists (International Contributions to Hydrogeology 16),Verlag Heinz Heise, Hannover, 1994.106.

[3] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2000:78～101.

[4] 谢乃明,刘思峰.离散GM(1,1)模型与灰色预测模型建模机理[J].系统工程理论与实践,2005(1)：93～99.

[5] 王应明. 运用离差最大化方法进行多指标决策与排序. 软科学研究, 1998（3）：36～38，65.

[6] 孙才志,林山杉.地下水脆弱性概念的发展过程与评价现状及研究前景[J].吉林地质，2000, 19 (1): 30～36.

[7] 吴登定,谢振华等.地下水污染脆弱性评价方法[J].地质通报,2005,24(10):1044～1046.

[8] Soutter Marc, Musy Andre. Coupling1D Monte-Carlo simulations and geo statistics to assess groundwater vulnerability to pesticide contamination on a regional scale [J].Journal of contaminant Hydrology，1998，32:35～39.

[9] 王国利,周惠成,杨 庆.基于DRASTIC的地下水易污染性多目标模糊模式识别模型.水科学进展,2002,11(2):173～179.

[10] Gogu R C, Dssargues A. Current trends and future challenges in groundwater vulnerability assessment using overlay and index methods[J]. Environmental Geology,2003,39(6):549～561.

[11] 周 磊.北京城近郊区地下水脆弱性研究[D].吉林大学硕士学位论文,2004.9.

[12] 雷 静.地下水环境脆弱性研究[D].清华大学硕士学位论文,2002,11～14.

Abstract:The different engineering geological problems of foundation pit excavation will occur in the different geological-engineering condition. In this paper, the author discusses the different geologic problems during excavating the foundation pit, and puts forward the detailed countermeasures in a foundation pit project in Xi’an City.

Keywords:groundwater flow into foundation pit; side slope slippage; settlement; timbering; precipitation

Application of the Method of Gray Correlation in Groundwater Vulnerability Assessment and Partitioning

SUN Fengying1, Xu Guangquan1,Tang Wenfeng2
(1. Anhui University of Science and Technology, Huainan, Anhui 232001. 2. Huainan Union University, Huainan, Anhui, 232038 )

The Grey Correlation Method is employed to analyze the vulnerability of groundwater. This paper established an assessment index system, which was made up of the depth to groundwater, impact of the vadose zone, aquifer thickness, net recharge, groundwater quality, and pollutant headwater. The weight allocation is more reasonable by applying the method of maximizing deviation to determine. Moreover, based on the MATLAB, it developed several calculation programs. On the attempt to assess and partition the groundwater vulnerability in Fuzhou City of Jiangxi Province, the result is satisfactory.

gray correlation;groundwater vulnerability;index system; maximizing deviation method

Research on Geologic Problem and Countermeasure of Foundation Pit for a Excavation Project in Xi’an City

GUO Zhifeng
(Shenzhen Construction Engineering Group Co. Ltd., Shenzhen, Guangdong 518048)

P641

A

1007-1903(2009)03-0032-04

孙丰英(1979 -),女,安徽理工大学水文系教师，主要从事环境地质、水文地质方面的教学和科研。