基于强度折减系数法的基坑数值仿真分析

2009-03-28付建军贾柠骏吴晓旺

城市地质 2009年3期

赵川，付建军，贾柠骏，吴晓旺

（1.武警交通直属工程部第一工程处,北京 102101;2.中国科学院武汉岩土力学研究所，武汉 430071; 3.湖南省吉首市保靖县规划办,吉首 416500 ;4.中铁五局建筑公司遵义第五分公司，遵义 563000 ）

基于强度折减系数法的基坑数值仿真分析

赵川1，付建军2，贾柠骏3，吴晓旺4

研究表明，由极限平衡法确定的滑动面、安全系数存在一定误差，强度折减法以弹塑性力学为基础，能准确给出真实稳定系数的下限。本文以武汉某基坑为例，以强度折减法为基础，采用flac软件进行数值仿真分析，提出了基坑支护的方法，经过工程验证，达到了预期的支护效果。

极限平衡法；强度折减法；稳定系数；仿真分析

0 前言

经典极限平衡分析法的缺点主要是只适用于均质材料，并且通常是根据边坡岩体的结构等特征，假想一个滑动面作为危险滑动面，从而计算该假想滑动面相应的稳定安全系数。然而，现实中几乎没有均质的土体，而且计算中要假设多个危险滑动面进行稳定安全系数的计算，用平面、折线、楔形、圆弧形等常规的滑动面形式无法反映基坑滑动的真实状态[12]。

为了克服和弥补经典极限分析法的不足，一种方法是采用弹塑性极限平衡分析法。弹塑性极限平衡法从分析边坡体的应力和变形入手，由边坡体的应力和变形特征来确定边坡体的极限平衡状态，从而避免对边坡体最小安全系数的反复计算及比选，达到减少工作量和提高准确率的目的。弹塑性极限平衡法中采用强度折减法，在地质条件、材料参数、屈服准则和本构关系正确的前提下，能够保证由此得到的稳定安全系数为真实稳定安全系数的下限。弹塑性极限平衡法不必假设土条间的作用力与破坏面的位置和形状，因此，该方法能处理复杂几何轮廓和边界条件，有广泛的适用性和良好的应用前景[3][8]。

1 强度折减系数法

1.1 基本原理

强度折减系数法认为外荷载保持不变的情况下，边坡内土体所发挥的最大抗剪强度与外荷载在坡内所产生的实际剪应力之比，外荷载所产生的实际剪应力与抵御外荷载所发挥的最低强度即按照实际强度指标折减后所确定的，实际中得以发挥的抗剪强度相等。当假定边坡内所有土体抗剪强度的发挥程度相同时，这种抗剪强度折减系数定义为边坡的稳定安全系数，由此所确定的安全系数可以认为是强度储备安全系数。在地基极限承载力与传统边坡稳定性分析中，所采用的传统安全系数一般是指荷载增大系数。

1.2 基本假设

（1）边坡岩、土体为理想的弹塑性材料，且本构模型为摩尔－库仑准则。

（2）失稳判断标准：塑性区贯通即利用图形可视化技术绘制边坡内广义剪应变的分布图,如果在某一折减系数下,土体内某一幅值的广义剪应变自坡脚底部下方向坡顶上方贯通，则认为此前的折减系数为安全系数。

1.3 折减参数分析

强度折减系数法的基本原理是将土体参数C和φ值同时除以一个折减系数F，得到一组新的C'和φ'值，然后作为新的材料参数进行试算。当边坡处于临界状态时，即F再稍大一些，边坡将发生破坏，对应的F被称为边坡的稳定性系数。此时土体即将发生剪切破坏，即计算结果是指达到临界状态时的折减系数F，具体公式为：

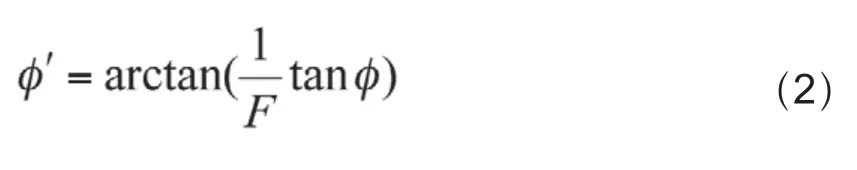
2 数值仿真分析

2.1 工程概况

同时我们亦发现少数BF+，AI-2-菌株存在，说明形成BF的形成可能存在其他调控通路。我们推测AI-2信号是促进BF形成的条件之一，但不是全部条件，CRS表葡菌BF的形成应该是多通路共同调节。本研究也证实无论何种通路形成BF，鼻渊舒口服液均可有效拮抗。

武汉某基坑工程开挖深度8.0m，周边环境条件简单，拟建场地土层如下，①杂填土，厚度1.6m；②淤泥，厚度2.4m；③粘土，灰褐色—黄褐色，饱和硬塑，厚度2.8m；④粘土，黄褐色，饱和硬塑，厚度2.9m；⑤粘土，黄褐—棕红色，局部夹砾石；厚度10m。根据勘察报告，不考虑地下水的影响。

2.2 模型及参数选择

计算模型取高度为17.7m，建筑长度取34m，见图1、图2，各土层的计算参数见表1，采用1:1的坡率放坡，计算所得安全系数。

图1 基坑模型

图2 边界条件

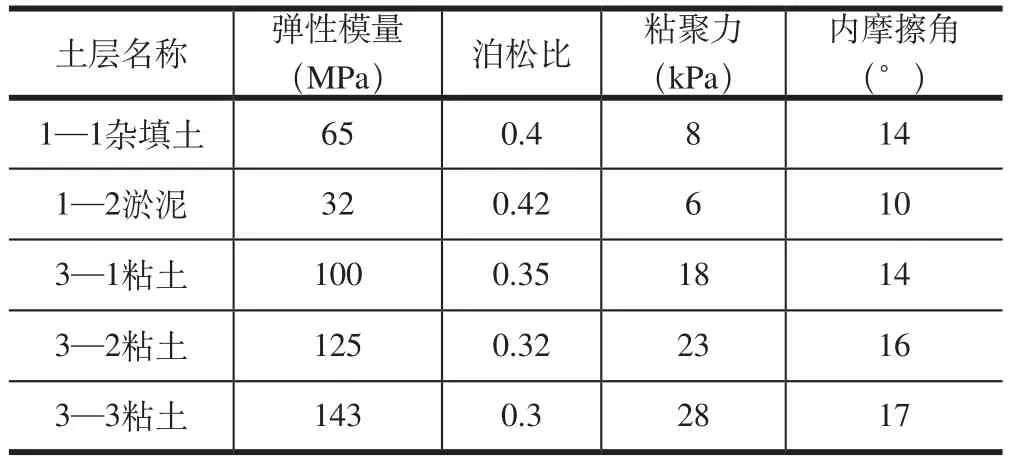
表1 仿真分析计算参数

2.3 安全系数稳定分析

Flac软件数值仿真分析结果见图3，极限平衡法分析结果见图4，由图可知，强度折减法计算的最小安全系数0.93，极限平衡法计算所得最小安全系数为0.801。安全系数区别的原因在于强度折减法考虑了土体强度与变形的关系，能更真实反应土层位移、应力场；两种方法都认为基坑最危险滑动面发生在基坑上部，且滑动溢出边界面处在淤泥土层中，认为此基坑不会发生深层滑动。

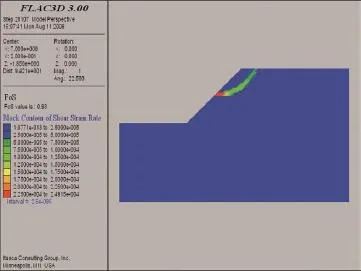
图3 强度折减法安全系数

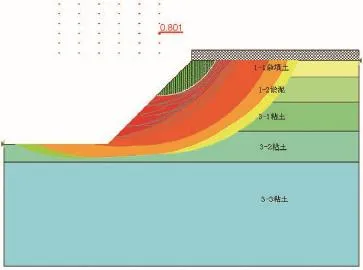
图4 极限平衡法安全系数

2.4 基坑安全稳定控制措施

为了保证安全生产、控制基坑变形，拟采用以下方案：

(2) 在坑边土体2 3m范围内喷射混凝土进行硬化处理，使邻空面土体形成整体稳定性；

(3) 由计算结果判定基坑很难产生深层滑动，整个基坑采用1：1放坡并对坡面采用喷射混凝土＋1m短土钉护面。

(4) 在基坑底面、顶面设置明沟排水；

工程实践结果证明，采用以上方法进行基坑支护，能实现预期支护效果。

3 结语

（1）极限平衡法属于刚体力学范畴，强度折减法属于变形力学范畴，由于它考虑了土体强度与变形的关系，因此理论上能更真实反映出安全系数的理论精确解。

（2）强度折减法和极限平衡法都是以摩尔－库仑强度准则为基础，都认为土体发生破坏主要是由于抗剪强度不够，因此可以采用注浆、打锚杆等措施来增强土体自身、滑动面上抗剪强度。

（3）表层喷射混凝土，使土体由二向应力状态变为三向应力状态，土体抗剪强度明显增加。

[1] GB 50007—2002 建筑地基基础设计规范.

[2] 赵明阶,何光春,王多垠.边坡工程处理技术[M].北京:人民交通出版社,2003.

[3] 张鲁渝,郑颖人,赵尚毅等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003,(1):21～26.

[4] 赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座—Ⅱ有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332～336.

[5] 迟世春,关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性[J].岩土工程学报,2004,26(1):42～46. [6] 陈祖煜.土质边坡稳定分析原理·方法·程序[M].北京:中国水利水电出版社,2003.

[7] 栾茂田,武亚军,年延凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1～8.

[8] 郑颖人.岩土材料屈服与破坏及边(滑)坡稳定分析方法研讨[J].岩石力学与工程学报,2007, 26(4): 649～661.

Numerical Simulation of Foundation Pit Based on the Shear Strength Reduction

ZHAO Chuan1, FU Jianjun2, JIA Ningjun3, WU Xiaowang4
（1.The First Engineering Section of Traffic Engineering Sector Directly Under the Armed Police Force, Beijing 102101; 2. Institute of Rock and Soil Mechanics, CAS, Wuhan, Hunan 430071; 3. Jishou City, Hunan Province Baojing Country Planning Office, Jishou 416500 4.The Fifth Subcompany of China Railway No.5 Engineering Group Co. Ltd, Zunyi, Guiyang 563000）

The related studies show that the stability coefficient and sliding surface acquired by limit equilibrium method are lack of trueness. Shear strength reduction based on elastic and plastic mechanics can give the lower limit of the realistic stability coeffcient. This paper takes the foundation pit in Wuhan as an example; the numerical simulation is done by the Fast Lagrangian Analysis of continua (FLAC) according to shear strength reduction; at last puts forward a support method for the foundation pits. The engineering practice has proved the support method up to the anticipation effect.

limit equilibrium method; shear strength reduction; stability efficient; numerical simulation

TU431

1007-1903（2009）03-0029-03