低年级数学学习过程中的错误原因例析
2009-03-27朱宇
朱 宇
这是一些屡屡出现的错误:44-19=35,36×2=82,29÷3=8……5,如此等等。我们在痛心疾首之余,往往会疾言厉色地批评这些错误的小主人“太粗心”。由于低年级儿童的感知具有笼统、不精确的特征,因此在数学学习过程中经常出现这些“低级错误”。这些“低级错误”真的可以用“粗心”一言以蔽之吗?或者说,我们真的可以把产生这些错误的原因全部诿过于学生吗?
在此,笔者试从儿童数学学习的特点,结合平时的教学实践,对“粗心”背后的原因向自己,也向广大的数学教师叩问——
一、 学生存在学习障碍吗
1.言语障碍
对低年级学生而言,阅读理解能力是解决数学问题的必要前提。小学数学应用题中的词汇有些是数学中的专门术语,有些则是生活中的日常用语。因此,指导学生准确理解这些词汇的内涵是正确理解问题的前提。
例如,有这样一道图文应用题:图书室原来有500本故事书,1班:我们班要借200本;2班:我们班要还150本。现在图书室有多少本故事书?
这样一道加减混合的应用题(500-200+150),许多学生笔下列出的却是连减算式:500-200-150,问及缘由,着实令人哭笑不得:原来,二年级的学生还不能准确地掌握“还”字的两种读音,把题目中的“要还(huán)”误读成“还(hái)要”,阅读理解的偏差造成了解题思路的错误。
“‘60比15多得多,这句话还可以怎么说?”
“15比60少得少。”
学生由“多得多”想到“少得少”,其实并不是类推的结果。这其中生活经验的作用被忽视了。因为在后面的练习中,学生都很流利地说出“小红比小明矮得多”、“小华的岁数比爷爷的岁数小得多”,完全没有出现“矮得矮”、“小得小”这些不合规矩的说法。
数学上像这些约定俗成的表示方法,它们与生活联系密切,如果在教学中不注意两者的有机整合,也会给学生的语言表达带来麻烦。
2.认知欠缺
如果不是亲耳听到这位同学的解释,我怎么也不会相信存在这样的算法:
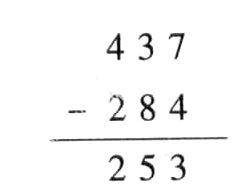
“个位上用7减4得3,十位上用8减3得5,百位上用4减2得2。”
“十位上为什么用8减3呢?”
“减法,就是用大的减去小的。”
天哪,如果不多问一个为什么,我们还会不厌其烦地告诉他和他的同学们:十位上3减8不够,向百位借走了“1”,所以百位上应该算3减2得1。
可他是这样想的吗?根本没有!那么他怎么听得进我们的指导呢?正确的认知建构是避免错误的前提条件。
3.技能生疏
计算过程中失误连连,根本原因在于学生没有形成纯熟的运算技能。因此我们必须帮助学生实现计算行为的自动化。因为口算既是笔算、估算和简算的基础,也是计算能力的重要组成部分。在教学中,要做到每堂课上安排口算训练,形式可以包括听算训练、视算训练、抢答、“开火车”等。此外,还应该鼓励学生参加必要的社会实践,比如让学生随父母上街采购物品时,帮助家长口算价款。
因为低年级学生注意力差,所以,老师在课堂上一般不敢让学生打开课本,认为学生看了课本后,什么都知道了,就不会认真听课。实际上,由于低年级学生识字能力不强,对文字本身的含义理解不够深刻,更加难以理解隐藏在文字背后的数学知识,难以领悟其中的密切联系。因此,低年级老师更应该指导学生有效地进行数学阅读,在阅读的基础上展开数学课堂教学。
二、 教师指导到位了吗
1.怎能如此武断
课上,一位学生计算36×2时把结果写成了82。教师审视了其运算竖式,指着这“显而易见”的错误,谆谆告诫这位学生,以后不能如此粗心。该生虽说满脸通红,低着头,口里却小声嘀咕着什么。看样子,他挺有意见。
其时,笔者正在课堂上听课,发现这位学生的书写过程确实没错,于是悄悄地请他说说算理“二六十二,写二进一;三加一得四,二四得八”。
原来如此!我小声地给他指出了他运算顺序上的错误之处,十位上应先算2个3,再加上1,得7,结果是72。
学生在计算过程中发生的错误,确有粗心造成的,这涉及学习习惯与意志品质的培养,这里且不提它。但是,更多的错误,却各有其产生的原因,有的是因感知错误,导致法则出错;有的是因旧知识的干扰,而产生的痕迹性错误;有的是因概念模糊而产生的错误。
我们常教育学生说:学习知识,不仅要知其然,更要知其所以然。那么,身为教师的我们,在对待学生计算中的错误时,又何尝不应如此呢?我们做教师的不仅要“明其错”,更要“明其何以错”,方能让学生找到错误的根子,及时对症下药。否则,同样的错误还会在同样的地方继续出现。
2.为何不能“坐下来看”
这是我的一次亲身经历。
在 “观察物体”这一课的课前,我给每桌准备了三个同样大小的正方体,让他们课上拼摆、观察。
投影出示:如图1,先摆一摆,再画出从侧面看到的图形。
经过一番操作、观察,学生画出的图形让我大吃一惊。
学生几乎都画出了图2。
我很感意外:没道理呀,从侧面看到的图形应该是图3。让学生再观察,但是学生仍然坚持自己的意见。

我刚准备说些什么,这时,小红同学大声地对我说:“老师,你坐下来看!”
坐下来看?我边琢磨着,边来到小红的座位旁边。
小红站起身,把她的座位让给我。
位置太小,很不舒服,真难为他们了!与我视线的水平线相比,小正方体位置太低,我只得把头向右侧过去
我愣住了:眼前看到的分明是图2,原先水平的两个图形竟然“立”了起来。
我一下子全明白了:从侧面看,不等于侧过头看。侧面与正面的区别不等于视角的“侧”与“正”,而在于观察者是否以身体正对物体的侧面,视线是否垂直于物体的侧面。
在我们成人的“想当然”中,把“侧面”“正面”理解得非常简单,其实,这当中的细节因素,如视角的调节、位置的移动等就很值得研究。然而,我只是笼统地提出一个“粗糙”的要求。
我们平时常常挂在嘴边的一句话是:站在孩子们的角度看问题。然而,我们却常常不自觉地以自己的思维替代孩子们的思考,以自己的主观臆断推测孩子们的客观认识。
3.不该“无心误导”
课上,认识完整时后,教者把分针拨到12过了一点点,这时时针自然也过了“8”,看着这时的钟面,师生共同找到了表示这一时刻的方法——大约8时。以同样的方法学生又认识了“大约1时、10时”……
从“几时”到“大约几时”,似乎大功告成。然而,当教师把分针拨到12左边一点点时,指着时针(6不到一点)提问,学生的回答把教师吓了一跳:小约6时。
竟然还有“小约”几时。
是孩子们在信口胡言吗?不是,他们错误答案的背后还有推理过程呢:既然分针过了12多一点叫大约几时,那么,相应地,分钟不到12,当然被称为“小约几时”了。
错误的缘起在于教师推介材料的不当。须知,“大约几时”是相对于整时出现的一个模糊概念,应该包括“整时多一点”和“整时差一点”,两者之间是并列关系,并无先后关系。材料呈现时机的不当造成了学生认知上的“先入为主”。
三、 你有长远的眼光吗
1.提倡一次做对
犯错后及时纠错,这是对的。但总是做“事后诸葛亮”并不是明智之举。我们应要求学生一次做对。比如,要求学生对于所抄写下来的题目都进行认真校对,细到数字、符号,不错不漏。看清题目中的每一个数据和运算符号,确定运算顺序,选择合理的运算方法。规范书写,做到书写工整、格式正确、字迹端正。另外,要教给他们验算和估算的方法,并将验算作为计算过程的一个重要环节进行严格要求。
2.培养反思意识
对学习过程中表现出来的错误,我们不能简单地下判断,可以“将错就错”,要求学生观察、分析,自行找出错误的原因,不仅“明其错”,更要“明其何以错”。很多时候,学生在探索过程中不一定都能获得对错误的体验,因此,作为处于主导地位的教师,有时可以巧设“陷阱”,让学生于不经意间“上当”一回,从而有效地弥补探索过程中的体验不足。在解决问题的过程中,我们还应该经常这样问学生:想一想,你为什么没有得到问题的答案?这个问题之所以没能得到解决,主要原因在哪里?怎样修改就可以了?
