巧用多媒体 让数学思想成为学生思维发展的助推器
2009-03-13殷国伟
殷国伟
数学思想方法是人类思想文化宝库中的瑰宝,是数学的精髓。《数学课程标准》在总体目标中提出:通过义务教育阶段的数学学习,使学生能够“获得适应未来社会生活和进一步发展所必需的重要数学知识(包括数学事实、数学活动经验)以及基本的数学思想方法和必要的应用技能”。在小学数学教学中,教师有计划、有意识、有步骤地渗透一些数学思想方法,是未来社会的要求和国际数学教育发展的必然结果。正是基于这种考虑,现行苏教版教材从四年级开始把“解决问题的策略”作为独立的一个单元进行教学。“形成解决问题的一些基本策略,体验解决问题的多样性,发展实践能力和创新精神。”
然而在实际的教学过程中,我们发现很多教师在教学这一单元时为了策略而策略,仅仅着眼于“解决问题”,追求某一类型题的能解会算。我们认为:新教材之所以增加这类内容,其目的不仅在于要让学生“学会做这些题”,获得这些问题的结论与答案,更在于让学生经历并体验每一种策略的形成过程,获得对策略的认识与理解,感受策略给问题解决带来的便利,真正形成自觉运用策略的意识。下面就通过国标本苏教版数学教材六年级下册《解决问题的策略》谈谈如何运用多媒体让数学思想在解决问题中发挥其作用。我们在充分理解教材编写意图后对单元教学内容从整体上进行了构思,进一步丰富了教与学的素材,并根据教学实际增设了第三课时的教学,现采撷几个教学片断。
●转化的思维方法
如果不“变化问题”我们几乎不能有什么进展。转化应该是数学教育过程的核心——用基本的和一般的观念来不断扩大和加深知识。
——G.波利亚
【片断1】
1.[练习题]
求下列各图形的阴影部分面积,都需要用到转化的策略吗?分别说一说。

(学生均认为第1、2幅图都不需要转化,能直接求出阴影部分面积,而第3、4幅图均需要转化,并说出了具体如何转化。)媒体的出现很好地解决了静状思维,通过化静为动,让学生直观地感知转化对解决问题的帮助。
2.[练习题]
A.一种盐水中,盐的含量是水的1/9,810克这样的盐水中,含盐多少克?
B.一种盐水中,盐的含量是盐水的1/10,810克这样的盐水中,含盐多少克?
学生独立练习,部分学生到黑板上板演。(学生在解答时进一步明晰了何时需要用转化的策略:当题中“未知量”与“已知量”没有直接关系时,一般要用“转化策略”进行解决。)
师:遇到比较难的应用题时,对关键句进行合适的转化是解题的关键。
3.转化下列关键句
(1)男生人数是全班人数的3/7。
(2)学校饲养小组养的白兔与黑兔只数的比是4︰5。
(3)学校十月份的用电量比九月份节约了10%。
(此环节引导学生从部分与部分,部分与总体以及分数、比、百分数等不同的形式方面考虑,让学生进行了多角度思考,有效实施了转化。)
【解读】
本练习通过媒体“需要转化”与“不需要转化”的图形及应用题的对比,引导学生在比较中体悟转化策略的应用情境,在反思中形成自觉运用转化策略的意识。就转化的思维方法而言,应该分为“需不需要转化”、“转化什么”、“怎么来转化”三个层次来考虑,就图形的转化求面积、周长来说,因为其具有很强的直观性,也很难归纳出一个具有典型代表意义的方法,因此,第一环节的设计仅仅停留在“要不要转化”上,并不需要学生解决之。而应用题中的转化则是比较典型的,也是学生在后续的学习中会经常遇到的,所以在第二环节的教学中重点分“需不需要转化”、“转化什么”、“怎么来转化”三个步骤引导学生掌握转化的一般思维方法。如果说第
一环节仅仅是转化意识渗透的话,那么第二、三环节则是扎扎实实的能力、方法的训练。
●数形结合的思维方法
数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离。
——华罗庚
【片断2】
1.媒体出题:6+7+8+9+10+11+12+13+14+15=
师:此题你会做吗?如何思考?
生:会,用(6+15)×10÷2=105,也就是用等差数列求和公式来求。
师:真厉害,都能用公式求和了。刚才你说的这个公式,老师小时候也学过,但总是忘记,你们有没有好方法帮助我记住呢?
生1:可以借助图形来帮助理解记忆。
生2:对,我们可以把它转化成正方形图来求和(学生尝试,但未成功)。
师:你们的想法很好,思路很开阔。的确,很多计算题有时是能借助图形来理解和解决的,但你们都想到了用“正方形”,是受第一节课内容影响了吧!(生表示赞同,教师同时用多媒体由最上面一层6个小圆、第二层7个小圆……依次呈现出了如下梯形)。
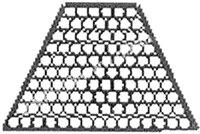
生3:我们所说的求和公式中的“首项”即相当于梯形面积公式中的“上底”……(众生恍然大悟)
生4:今后我们再也不会忘记“等差数列求和公式”了,它就跟我们学过的梯形面积公式差不多。(喜形于色)
生5(抢说):我发现了,今后如果遇到不会的计算题可以想能否“转化”成图形来解决。当然,不一定都是转化成正方形,也可以转化成梯形,也可能转化成圆……(众生笑)
2.媒体再现教材P72中的“试一试”,题目如下:
1-1/2-1/4-1/8-1/16=
师:看了这道题,你打算怎么做?(通分)对,通分也是一种转化的方法,把异分母分数转化成同分数分数。那有没有更好的方法呢?(学生分组讨论)
学生很快想到可以用图形来帮助分析、思考,具体如下:

学生到实物投影仪上展示了上图,并说出了理由:大正方形就相当于数字“1”,左半部分表示减去了1/2……(汇报后,教师又组织学生进行了充分交流)。
师:根据同学们刚才的发现,你们能很快说出下列算式的结果吗?(多媒体出示)
1-1/2-1/4-1/8-1/16=
1-1/2-1/4-1/8-1/16-1/32=
1-1/2-1/4-1/8-1/16-1/32-1/64=
……(学生很快说出了上面算式的结果)
师:观察这些算式与结果,你们有什么发现?
生1:每一个算式中的结果与最后一个减数都相同。
生2:结果相同的原因是可以把上面的每一个算式都与正方形结合起来思考,图形中剩下的部分就是与最后一次要减的部分同样大。
生3:上面算式的结果越来越小,好像越来越接近0了。
师:你太棒了,那老师想请同学们想想,像这样减下去,结果会等于0吗?
(教室里出现了学生们发自内心的小声争论,但一会儿,学生们即统一了意见:这个结果会越来越接近0,但永远也不会是0。)
师:这个有意思的现象很早以前就有人发现了。2300多年前,庄子就说:“一尺之棰,日取其半,万世不竭。”(媒体呈现)你能解释这句话吗?
【解读】
数形结合思想的实质,就是将抽象的数学语言和直观的图形结合起来,通过媒体化抽象为直观来深化数学内容,实现抽象与形象的联系与转化。“数缺少形时少直观,形少数时难入微。”本教学设计利用媒体把枯燥的数(算式)转化成规则的图形,使学生在体会数学美妙一面的同时,也充分感受到把数形结合的直观性与便捷性,有效沟通数学知识之间的联系,凸显数学的本质特征。作为一种策略的选择,或者说一种思维方法的渗透,我们关注的不仅仅是要解决某一个具体的数学问题,更重要的是让学生在这一过程中体验到数学的多姿多彩、五彩斑斓,并能自觉运用这种思维方法观察、分析、解决数学内、外的各种问题。
●归纳的思维方法
归纳这种方法……选出一个类似的、较易的问题,去解决它,改造它的解法,以便它可以用作一个模式。在外人看来似乎是迂回绕圈子,但在数学上或数学以外的科学研究中是常用的。
——G.波利亚
【片断3】
[练习题]
有4支足球队参加比赛,比赛以单场淘汰制(即每场淘汰1支球队)进行。一共要进行多少场比赛后才能产生冠军?如果是64支球队呢?(第二问稍后出示)
[练习过程]
1.这样的题你能画出示意图吗?(指导学生用树形图表示)
2.学生画图。(大部分学生应该很容易地得出是3场比赛)
3.出示第二问。如果是64支球队呢?还想画图吗?
4.学生思考后,教师引导:遇到这种比较难的、数字比较大的题,我们可以先找几个数学比较小的题进行尝试,得到规律后再解决原来的题。
5.学生用画树形图的方法,自己独立解决8支球队、16支球队需要进行多少场比赛。
6.刚才我们分别解决了4支、8支、16支球队比赛需要的场数。你发现什么规律了么?(学生说规律:需要的场数比球队数少1)
7.现在你知道64支球队需要比赛多少场了吗?你是怎么想的?
8.还可以怎么想呢?
引导(转化思路):每进行一场比赛淘汰一支球队,64只球队需要淘汰掉63只球队才能决出冠军,所以一共需要进行63场比赛。
9.小结:转化的不仅仅是图形、关键句,更重要的是对思路的转化。
【解读】
不完全归纳的思维方法是对若干个特殊事例的考察,从中归纳出一般性的结论的一种推理方法。为了让学生感受这种方法,在本练习中,让学生先从简单的做起,分别用画图的策略得到4支、8支、16支球队参赛时的场数,再推及到64支球队的情况。让学生完整地经历由一般到特殊,从简单到复杂,大题小做、归纳推理的方法,不但使学生的思维层次得到一次提升,更能促进学生从“学会”到“会学”的跨越。
总之“解决问题的策略”不仅仅是为了解决问题,而应该是以问题的解决为载体,通过媒体引领学生在操作中体验,在对比中反思,发展数学思维,初步形成用数学的眼光看待问题,用数学的头脑分析问题,用数学的方法解决问题的能力。在教学中,我们要善于捕捉数学思维的生长点,用数学思维撑起解决问题的脊梁,带领学生感受数学丰富的方法、深邃的思想,分享数学前行足迹中的创造、超越及其背后折射出的人类智慧和人性光芒。■
