基于离散单元法的裂隙岩体渗流与应力耦合作用机制研究
2009-01-29孙玉杰邬爱清张宜虎张家发
孙玉杰,邬爱清,张宜虎,张家发
1 概 述
对渗流而言,裂隙岩体是双重介质,岩块是孔隙介质,而由裂隙构成的网络体系是离散介质。对大多数岩石而言,完整岩块的渗透系数极为微弱,从工程角度可忽略不计,被认为水流只在岩体的裂隙网络中流动。由于裂隙常成组分布,因而裂隙岩体渗流往往具有明显的各向异性,不同方向渗透性差异很大。岩块的弹性模量很大,而岩体的变形模量要小很多,两者之间的差异反映了裂隙变形的影响。在正常荷载作用下,岩体绝大部分变形发生在裂隙部位。研究成果表明,裂隙的过水能力与隙宽的3次方成正比,裂隙宽度的微小变化,会在很大程度上改变岩体的渗透特性。因此,对裂隙岩体渗流场的研究,一方面应考虑应力环境对裂隙变形的作用;另一方面,裂隙的变形将改变岩体的渗流场,渗流场改变进而会影响裂隙的变形,这一过程的分析,即是在裂隙岩体条件下的应力场与渗流场的耦合分析问题。
目前,关于岩体渗流场与应力场的耦合研究,主要是连续介质条件下的研究成果[1-9]①②Louis C.Rock Hydraulics.Rock Mechanics.(edited by Muller L),udine 1974:299-387.。这里的连续介质包括两个含义:①将分析对象本身概括为连续介质,采用线性与非线性数值计算方法,研究岩体的渗流与应力耦合问题;②鉴于岩体裂隙的存在,对岩体渗透特性的重要影响,采用基于连续介质模型的数值方法,通过嵌入岩体中裂隙的本构模型,以实现裂隙岩体的渗流与与应力耦合。在这些研究成果中,关于因应力条件的改变而引起岩体中裂隙的张开、闭合与错动等裂隙几何非线性问题,未能考虑。
为在裂隙岩体渗流分析中考虑裂隙张开与闭合变形等几何非线性问题的影响,进而研究真正意义上裂隙岩体的渗流与应力耦合机制,这里以裂隙岩体中洞室开挖问题为研究对象,采用UDEC(Univer-sal Distinct Element Code)离散单元法中关于裂隙岩体开挖模拟及水力全耦合分析模型,分析裂隙岩体洞室开挖后,因围岩应力与水力耦合作用而导致的裂隙隙宽变化及渗流变化的过程,研究在有承压水条件下裂隙岩体洞室开挖过程中,裂隙岩体渗流与围岩中应力间的相互作用机制。
2 基于UDEC的渗流分析算法②
2.1 基本模型
利用UDEC水力全耦合模型来模拟裂隙中水的流动。UDEC是ITASCA公司开发的针对非连续介质的平面离散元程序,在数学求解方式上采用了与FLAC一致的有限差分法。对于水力全耦合的渗流分析,当水流主要是由裂隙网络控制时,UDEC程序是非常合适的。因此本文假设岩石基质是不透水的,水流主要通过水力连通的裂隙网络涌入隧洞内。UDEC中被裂隙所包围的岩块可以被模拟为刚体或者可变形体,通过域分析流体在裂隙中的流动。图1中将域顺序标号为①~⑤,假定域内充满各向等压流体,域和域之间通过接触与临域发生作用。接触顺序标号为A~F。域①、③、④表示节理,域②表示2个节理的交点,域⑤为空洞。
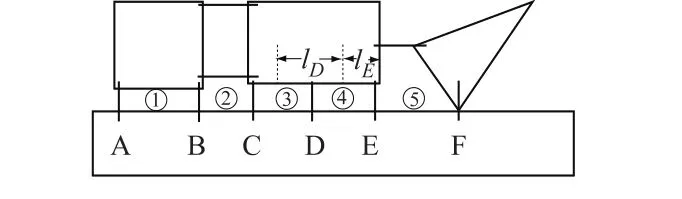
图1 通过域模拟流体在节理裂隙中的流动模型Fig.1 Flow in joint fissure modeled by flow between domains
不计重力时,假设流体压力在流动域中的分布是均匀的。考虑重力时,流体压力则按线性分布的静水压力计算。流体的流动是由相邻流体域的压力差决定的,其中流动域中流体压力的大小由流动域中的中心压力大小决定。
2.2 渗透流速计算
按块体接触条件的不同,裂隙岩体中流体的速率有2种计算方法。
(1)点接触。点接触分为角-边接触和角-角接触。设流动域①的流体压力为p1,流动域②的流体压力为p2,则由流动域①到流动域②流体的流速为

式中kC为接触处的渗透系数;
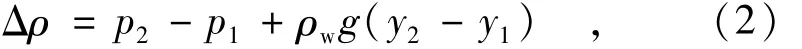
式中:ρw为流体密度;g为重力加速度;y1,y2为两个流动域的中心坐标。
(2)边-边接触。首先定义接触长度,图1中lD和lE分别为接触D和E的接触长度,然后利用平行板裂隙中的立方定律计算流动速度,即

式中:kj为裂隙的渗透系数(理论值为1/12μ,μ为流体的动力粘滞系数),l为两流体域之间的接触长度,a为接触的水力开度。
水力开度a由裂隙在无法向应力时的开度a0及在某法向应力条件下法向开度增量un组成,即:a=a0+un。假定法向开度增量un张开为正,压缩为负,水力开度的最小值为ares,最大值为amax。裂隙宽度随节理法向应力的变化如图2所示。

图2 水力开度a与法向应力σn之间的关系Fig.2 Relation between hydraulic aperture(a)and joint normal stress(σn)
2.3 裂隙水压力计算
计算过程中,每计算一个时步,重新生成系统的几何形状,而后计算出所有接触的裂隙宽度以及所有域的体积(对二维条件,取单位厚度),之后利用上面的公式计算出各接触处的流量。最后,迭加各接触点流入裂隙域的流体流量,并考虑由于周围块体的位移增量而产生的域体积的变化,按下式计算出域内的裂隙水压力。

式中:p0为前一时步的孔隙压力;Q为通过孔隙周围的所有接触点流入该孔隙的流量之和;kw为流体的体积模量;Δv=v-v0,vm=(v+v0)/2,其中,v和v0分别为现在时步和前一时步孔隙的体积,Δt为计算时步。
计算出域内裂隙水压力后,可以计算流体作用在其周围岩块的力。将该力与诸如接触点力和外力荷载等力迭加,施加在块体的节点上。这样就可得到不透水岩块的总应力以及节理的有效法向应力。
3 岩体渗流与应力耦合数值模拟
以裂隙岩体地下洞室开挖为例,研究裂隙岩体渗流与应力耦合作用机制。
3.1 几何模型及参数
本模型开挖地下洞室形状为马蹄形,隧洞宽4 m,高7 m,地下洞室顶拱中心距离地表300 m,并假定地下水位与地表面齐平。根据量测数据得到Ⅳ级结构面的统计参数见表1。根据地质资料,所采用的岩块及结构面的模型材料参数见表2所示。
根据经验,选定分析区域为44 m×44 m。依据表1中的Ⅳ级结构面的统计参数以及Ⅲ级结构面生成图3所示的结构面网络样本。依据结构面的交切关系,生成的连通水力网络如图4所示。
3.2 模型初始条件与边界条件
(1)初始条件。假定地下洞室顶拱中心距离地表为300 m,根据天然地应力场分布规律,可近似取铅直天然地应力为自重应力,并假设侧压力系数K铅直向应力分量随埋深增加线性增加。因此在顶拱中心位置,水平应力分量为12 MPa。

表1 Ⅳ级结构面样本几何形态统计结果Table 1 Statistical result of geometrical shape ofⅣ-grade structure samples

表2 模型材料参数Table 2 Material parameters in model

图3 结构面网络样本Fig.3 The structureal-face network molelling result

图4 连通水力网络Fig.4 The connective hydraulic network
(2)边界条件。由于地下洞室顶拱距离地表300 m,地下水位在地下洞室顶拱以上的高度相对地下洞室跨度而言足够大,可认为在地下洞室开挖过程中,岩体中的地下水位无变化,即洞室外边界水位为恒定水位状态。
洞室开挖模拟中,计算域外边界采用位移约束条件。
3.3 裂隙隙宽变化结果分析
计算结果表明,洞室开挖后,围岩中大部分裂隙受应力重分布影响有闭合发展趋势,只有少数裂隙处于张开发展趋势。裂隙的闭合使得结构面水力梯度变大,作用在裂缝上的渗透压力增大,促进导水裂缝扩展,裂隙连通性增加。裂缝张开度增大,渗透能力增强,渗流量增大,其渗流压力相应降低。
图5~9给出了隧洞开挖后,随着渗流的发展,洞周裂隙隙宽在应力渗流耦合作用下的变化过程。可以看出,由于开挖应力与渗流的耦合作用,与洞室相交的贯穿性裂缝,其隙宽有明显的增大趋势;在洞周附近,裂隙隙宽的变化比远离洞室要显著。
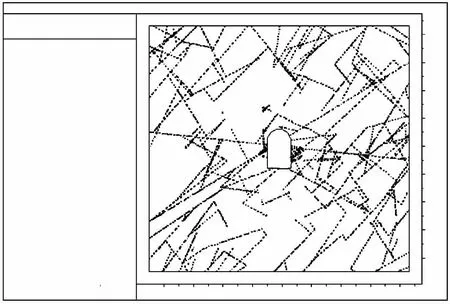
图5 洞室开挖完成1 s后裂隙隙宽Fig.5 Crevice opeining of cavity excavation after 1 second

图6 应力与渗流作用16 s后裂隙隙宽Fig.6 Crevice opeining of coupling action of stress and seepage after 16 seconds
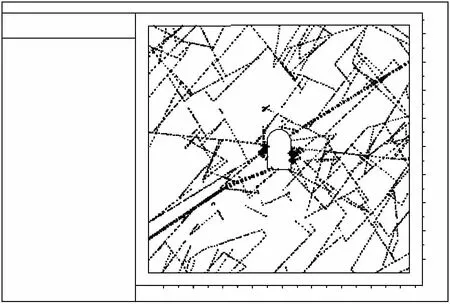
图7 应力与渗流作用36 s后裂隙隙宽Fig.7 Crevice opeining of coupling action of stress and seepage after 36 seconds
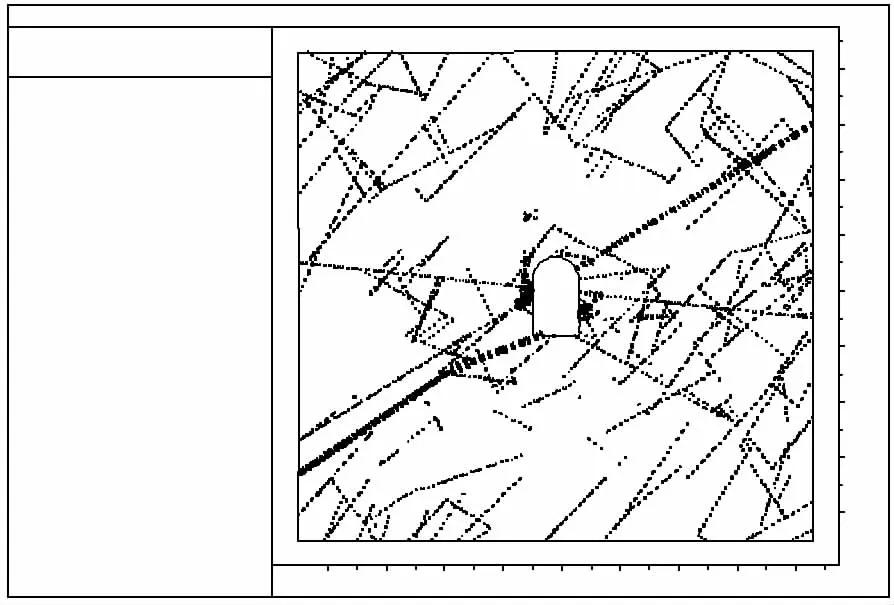
图8 应力与渗流作用76 s后裂隙隙宽Fig.8 Crevice opeining of coupling action of stress and seepage after 76 seconds

图9 应力与渗流作用136 s后裂隙隙宽Fig.9 Crevice opeining of coupling action of stress and seepage after 316 seconds
3.4 裂隙中水流量及水压力变化
为显示洞周围岩裂隙部位因隙宽变化引起的渗透压力与流量的变化过程,可根据节理裂隙与洞室围岩的切割情况,在洞周选取部分特征点作为监测点,根据监测点计算结果展示由于洞周隙宽的变化而引起的监测点处水流量与水压力发生变化的过程,进而反映洞周围岩裂隙中渗流与应力耦合的相互作用机理。
这里,选取洞室围岩中位于左边墙中部和位于洞室右边墙上部的2个特征点为监测点(监测点1和监测点2)。图10~13分别给出了上述监测点部位裂隙流量和水压力随时间的变化过程曲线。
从图10可以看出,位于左边墙中部点1处,在洞室开挖后,该处流量在逐渐减小,但是在水力耦合作用力裂隙隙宽逐渐变大。到15 s时水压力增加到2.7 MPa,流量发生突变时,该处最大流量达到4.46 m3/s。其后流量又开始减小,对应水压力开始增大,裂隙隙宽在水力耦合作用力下不断调整,对应水压力可由图11直观得出。每次流量的变化对应水压力均有变化。
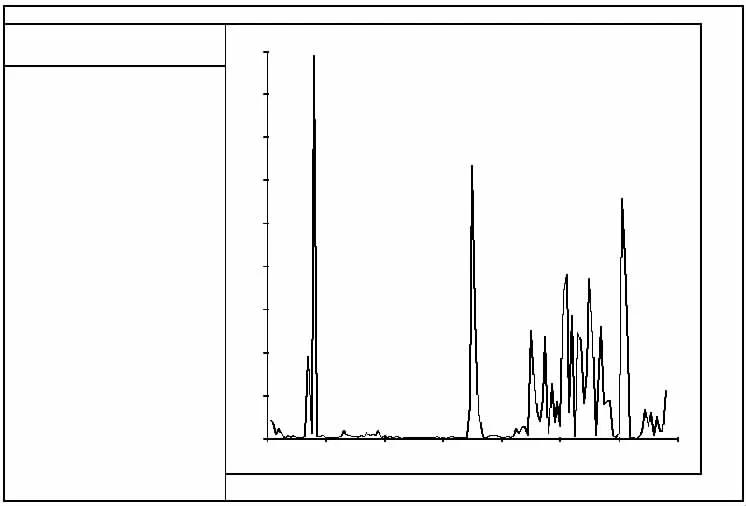
图10 监测点1处流量变化曲线Fig.10 Variation of the flow rate at the monitoring point 1
从图12可以看出:位于洞室右边墙上部监测点2在洞室开挖后的开始阶段流量逐渐减小,在渗流到 16 s时,流量变化达到最大,为0.734 m3/s,其后该处裂隙在水力耦合作用下逐渐闭合,流量逐渐减小;在渗流到39 s时,该处水压力降到零,这是因为该点所在块体发生脱离,且该点对应裂隙中没有水流因而流量降为零,此时,水压力也降为零。
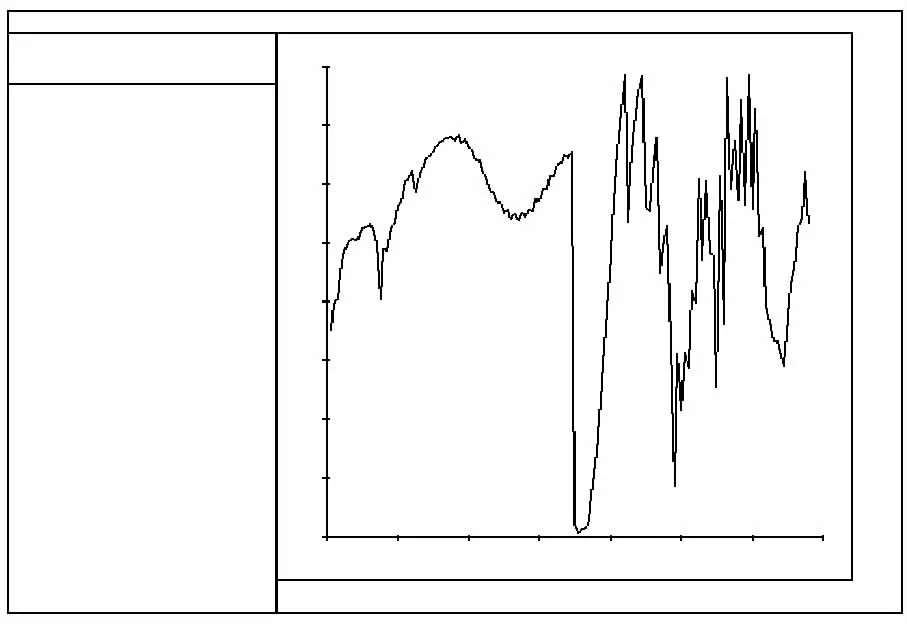
图11 监测点1处水压力变化曲线图Fig.11 Variation of the water pressure at the monitoring point 1
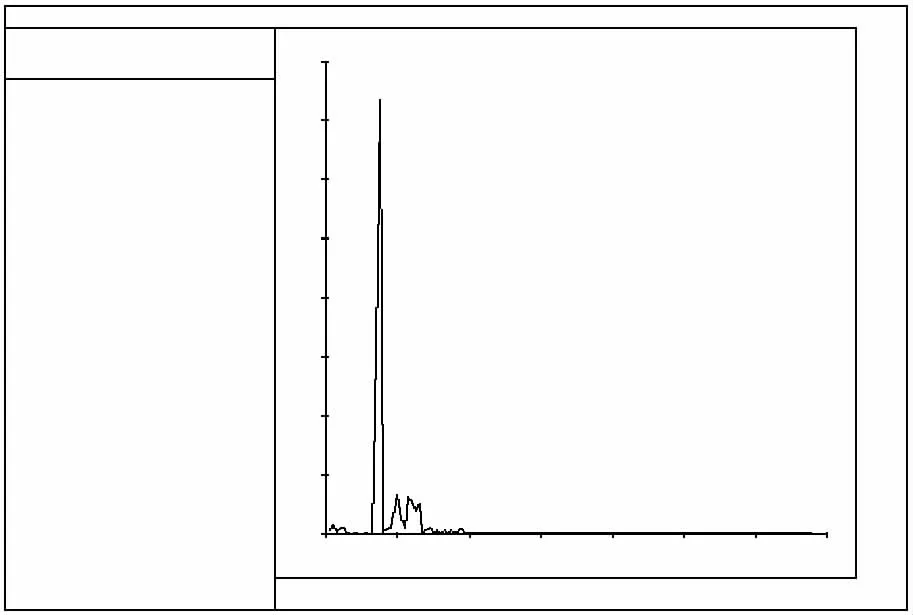
图12 监测点2处流量变化曲线Fig.12 Variation of the flow rate at the monitoring point 2
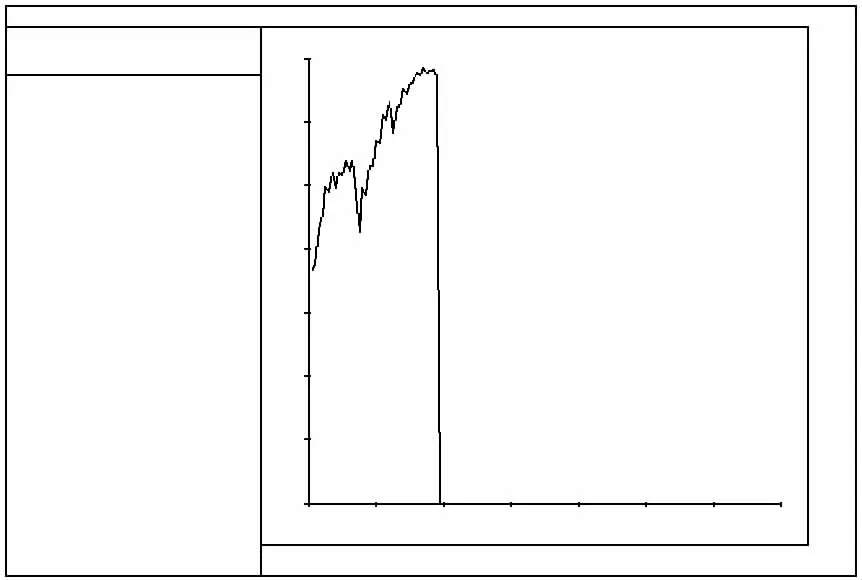
图13 监测点2处水压力变化曲线图Fig.13 Variation of the water pressure at the monitoring
4 结 语
本文以裂隙岩体中洞室开挖问题为研究对象,采用UDEC离散单元法中关于裂隙岩体开挖模拟及水力全耦合分析模型,分析裂隙岩体洞室开挖后,因围岩应力与水力耦合作用导致裂隙隙宽变化及渗流变化的过程。实例计算结果表明,洞室开挖完成后,在围岩渗流与应力耦合作用下,围岩中裂隙隙宽、裂隙中水压及其渗透流量的变化是一个动态过程,且相互作用与相互依赖。裂隙的闭合使得结构面水力梯度变大,作用在裂缝上的渗透压力增大,促使导水裂缝扩展,裂隙连通性增加。裂缝张开度增大,渗透能力增强,渗流量增大,渗流压力相应降低。
由于围岩中裂隙隙宽、压力和渗流量的动态依赖性,在一定条件下,裂隙隙宽的改变可导致局部水力通道的形成,高压水头从局部涌出,从而促进突水灾害的形成。
本文基于离散单元方法与程序,研究了因岩体应力环境的改变引起岩体裂隙的张开与闭合等几何非线性变形,进而引起岩体渗透特性与渗流场的动态变化,由此实现裂隙岩体渗流与应力耦合作用机制研究。研究成果初步表明了所采用方法的有效性,并为研究裂隙岩体中开挖洞室引起的突水问题提供参考。
[1] 忤彦卿.岩体裂隙系统渗流场与应力场耦合模型[J].地质灾害与环境保护,1996,7(1):31-34.
[2] 王 媛,速宝玉,徐志英.等效连续裂隙岩体渗流与应力全耦合分析[J].河海大学学报,1998,26(2):26-30.
[3] 陈 平,张有天.裂隙岩体渗流与应力耦合分析[J].岩石力学与工程学报,1994,13(4):299-308.
[4] 王 媛,徐志英,速宝玉.裂隙岩体渗流与应力耦合分析的四自由度全耦合法[J].水利学报,1998,(7):55-59.
[5] AYATOLLAHI M S.Stress-Fluid Flow Analysis of Frac-tured Rocks[J].J.of Eng.Mech.,1983,109(1):1-13.
[6] ODA,M.An Equivalent Continuum Model for Coupled Stress and Fluid Flow Analysis in Jointed Rock Masses[J].Water Resource Research,1986,22(12):3235-3246.
[7] 张有天.岩石水力学与工程[M].北京:中国水利水电出版社,2005.
[8] 忤彦卿,张倬元.岩体水力学导论[M].成都:西南交通大学出版社,1995.
[9] 陈洪凯.裂隙岩体渗流研究现状(Ⅰ)(Ⅱ)[J].重庆交通学院院报,1996,15(2):29-34.
