KL展开在渗流场随机分析中的初步应用

李少龙，杨金忠，张家发

为了准确反映土性参数的空间变异性，一般将渗透系数等参数作为空间随机场。将参数随机场和反映物理规律的微分方程相结合并发展相应的数值方法，成为随机分析的有力工具。文献［1］将渗透系数作为随机场，采用蒙特卡罗随机有限元法研究了土体渗透系数的随机性对有压渗流场统计特征的影响。文献［2］将渗透系数作为随机场，应用小参数摄动法得到稳定渗流的随机有限元列式，通过算例分析水力坡降标准差与渗透系数变异性之间的关系。以上分析仅考虑了一个参数的空间变异性，实际问题中通常是多个参数共同作用。

为了将参数随机场引入数值分析方法中，一般需要将随机场离散化。随机场的离散方法大体上可分为2类［3］：①空间离散，如中点法和局部平均法；②抽象离散，如 Karhunen－Loeve（KL）展开和多项式混沌展开。随着研究的深入，已经提出了许多求解随机问题的方法。蒙特卡罗模拟是在概念上比较直接的随机偏微分方程求解方法，但一般认为其计算量太大。摄动方法通常用于求解问题的一阶解，不适用于参数变异性较大的问题。文献［4］和［5］提出了联合运用随机场KL展开和摄动分析的KLME渗流随机分析方法，研究表明该方法具有较好的计算效率和精度。本文阐述参数随机场KL展开及其在渗流随机分析中应用的基本原理和特点，通过随机数值模拟，对饱和渗流场和多参数随机场条件下非饱和渗流场的统计特征进行分析。

1 随机场KL展开

随机场可以表示为级数展开，即用确定性函数的一个完备集与相应的随机系数来表征。在随机场的级数展开中，较为常用的是KL展开。随机场U（X，ω）的 KL展开式为

式中：珚U（x）为随机场的均值函数；｛ξi（ω）｝为零均值互不相关的随机变量序列；i（x）和 χi分别为随机场协方差函数C（x，y）的特征函数和特征值；x为空间坐标；ω为随机事件。特征值和特征函数满足第二类Fredholm积分方程：

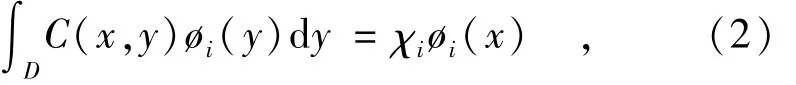
式中D为所研究的空间域。

由式（1）可知，随机场KL展开的关键是获得协方差函数的特征值和特征函数，它们满足方程（2）。对于定义在规则几何域上的一些协方差函数，可以得到其特征问题的解析解［6］。对于一般性问题，通常需要通过数值方法求解积分方程［7－9］，如迦辽金有限元法。

对任意分布的随机场，KL展开都是均方收敛的。在实际应用中，随机场的KL展开以有限项的截断形式近似表达，文献［6］证明该截断级数是最优的，即均方近似误差最小。这一性质表明只要利用随机场KL展开的少量展开项就可以表示随机场的空间相关信息，为KL展开应用于渗流随机分析提供了基础。KL展开既适用于平稳随机场又适用于非平稳随机场，适用范围较广，因而得到广泛关注。

2 基于KL展开的渗流随机模型

多孔介质中的稳定渗流可以用连续性方程和达西定律描述，

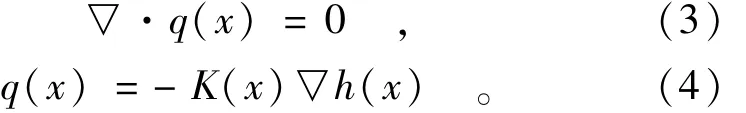
式中：q（x）为达西流速；h（x）为总水头；K（x）为渗透系数，在非饱和区它还是含水量或土壤负压的函数。根据具体问题给定相应的边界条件，那么就构成了渗流数学模型。实际上，渗流模型包含许多随机因素，这些可能因素包括：（1）模型中介质参数的不确定性，大量试验表明，含水层或土壤的渗透系数具有显著的空间变异性，即具有随机性和结构性；（2）模型中源汇项或定解条件的不确定性，文献［10］分析了降雨的随机特性对平面潜水流场统计特征的影响。由于模型包含众多不确定性因素，所以模型的解（通常是水头）也是具有一定概率分布的随机函数。本文仅考虑土体渗透参数的不确定性，将它们作为随机场，并采用上述KL展开离散化。

如果在渗流模型中只有一个参数随机场，记为f（x，ω），那么可直接根据KL展开将其分解为

式中：N为KL展开中保留的阶数，实际上也表示了概率空间中的随机维数，其余变量的意义同式（1）；f表示相应于参数场f（x，ω）。实际问题中还会有多个参数场的情形，基于KL展开的随机分析可以处理多个随机参数场的问题。为了简化分析，本文仅考虑2个参数随机场，记另一参数场为α（x，ω），将其展开为

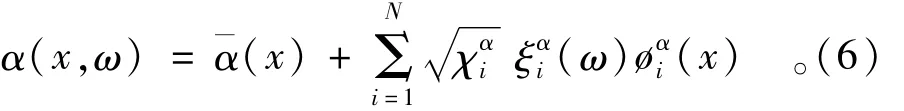
当模型中有多个参数场时，应考虑它们之间的互相关性。当参数场 f（x，ω）与 α（x，ω）不相关时，可分别按式（5）和式（6）将它们展开，此时随机变量序列｛ξfi（ω）｝和 ｛ξαi（ω）｝互不相关。当参数场f（x，ω）与 α（x，ω）完全相关时，即有线性关系 α＝af＋b，其中a和b为系数，由此可知它们的标准差满足关系式σα＝aσf。在此条件下，两参数场的KL展开式（5）和（6）可用同一随机变量序列，即 ｛ξfi（ω）｝＝｛ξαf（ω）｝。

文献［6］提出了谱随机有限元法（SSFEM），将系统输入随机场用KL展开，而系统输出则表示为Hermit多项式混沌展开，通过随机迦辽金有限元法推导了系统输出展开系数的微分方程组，由于这些方程是相互嵌套的，难于求解，当系统的随机维数较大时，计算量非常大。本文将水头展开为摄动级数，

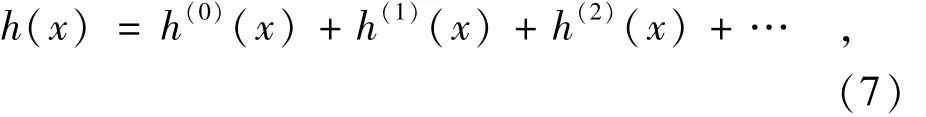
式中：h（0）为确定性的零阶展开项；h（1）和 h（2）依次为一阶和二阶摄动展开项。由于将模型参数作为随机场，待求水头的不确定性来源于参数的不确定性。当仅有一个参数场时，水头各阶摄动展开项可表示为［4］

当有2个参数场时，若它们是完全相关的，水头仍可按式（8）展开；若它们是不相关的，水头展开式可在式（8）的基础上增加随机维数而扩展得到［5］：

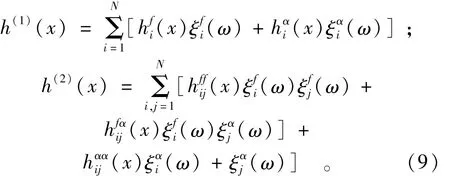
SSFEM和KLME方法都是将随机偏微分方程转化为待求变量展开系数的确定性偏微分方程组，进而数值求解得到研究问题的统计矩（如均值和方差）。然而KLME方法得到的偏微分方程组是一系列递推方程，由低阶向高阶依次求解，同阶方程的求解没有优先关系，可以逐个或并行求解。

3 算例分析

根据以上原理和方法，编写了渗流随机分析的Fortran程序，进行算例分析。首先考虑一个饱和流问题，取某堤坝的一个断面进行渗流计算，坝基为含水层，其下部为不透水层，由于坝体的透水性相对于坝基来说很小，因此假设坝体不透水。上游水位60．0 m，下游水位30．0 m。将渗透系数Ks作为对数正态平稳场，则对数渗透系数f＝ln Ks为正态场，均值 珋f＝－2．45（即 Ks几何平均0．086 4 m／d），协方差 Cf＝σ2fexp（－｜x1－y1｜／λ1－｜x2－y2｜λ2），方差σ2f＝1．2，考虑随机场的各向异性取相关尺度 λ1＝40 m，λ2＝2 m。对于不同具体问题，可以根据实测数据通过统计方法如地质统计学方法推求参数场的各统计量。

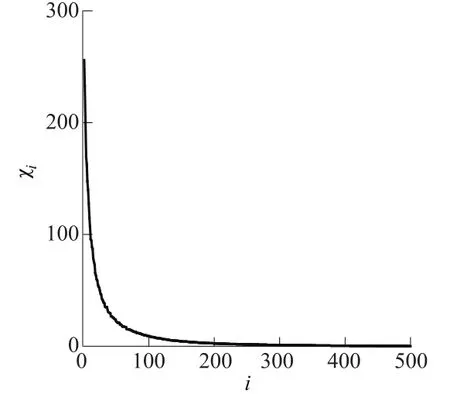
图1 特征值序列Fig．1 Sequence of eigenvalues

图1 所示为参数场KL展开的前500阶特征值，从图中可以看出，随着阶数的增加，特征值快速减小。在 KL展开中，较小特征值的展开项对整个随机场展开的作用不大，因而可以忽略。图2和图3分别显示了各阶水头展开系数，由图可见，二阶水头展开项在数值上比一阶水头展开项要小，几乎降低了一个数量级；对于同一阶水头展开，各展开项随着项数增加而减小，逐渐趋近于0。这一结果表明，水头的摄动展开具有渐进收敛性，用较低的阶数和较少的项数来近似表达水头展开是可行的。

图2 水头一阶展开项Fig．2 First order terms of hydraulic head

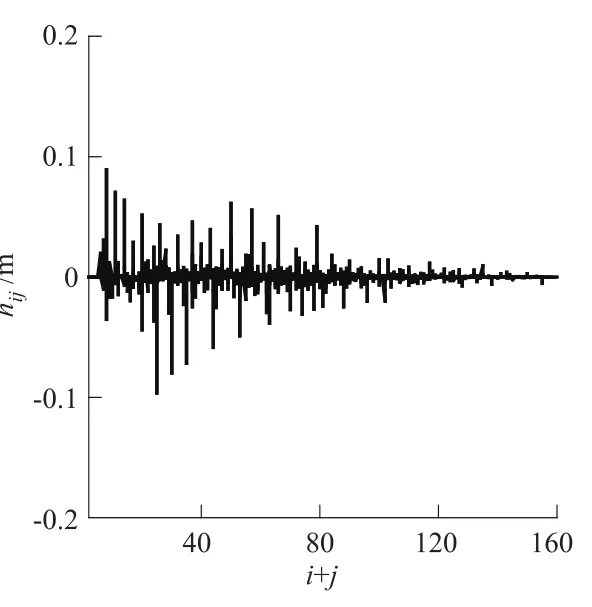
图3 水头二阶展开项Fig．3 Second order terms of hydraulic head

水头均值和标准差分别见图4和图5。从图中可以看出，水头均值在区域中部即坝体下方的下降较大，相应地水头标准差也在该区域出现极大值，说明水头的不确定性不仅与参数场的不确定性有关，也与渗流场的水流特征有关。由于大坝底部的上、下游边为确定性的水头边界，因而其水头标准差为零。水头标准差由定水头边界向区域中心逐渐增大，呈对称分布。

图4 水头均值分布图Fig．4 Distribution of mean head

图5 水头标准差分布图Fig．5 Distribution of standard deviation of head

下面考虑入渗达到稳定条件下土柱的非饱和渗流随机分析。为便于比较，非饱和渗透函数采用Gardner－Russo指数模型

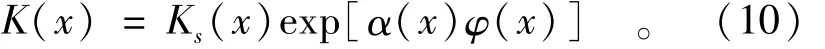
式中：φ（x）为土壤负压水头。将模型中的渗透系数Ks和孔隙大小分布参数α分别作为对数正态随机场和正态随机场。由于目前尚未对这2个参数的相互关性得到一致认可的结论，在一些非饱和渗流随机数值模拟中假设它们不相关，本文考虑对数渗透系数f和α不相关、正相关和负相关3种情况。采用文献［11］中的土壤数据，对数渗透系数的均值珋f和方差 σ2f分别为3．0（即 Ks几 何 平均 为20．1 cm／d）和1．2，孔隙大小分布参数的均值珔α和σ2α方差分别为0．07 cm－1和0．000 1 cm－2，相关尺度为50 cm。模拟土柱高度为1 000 cm，其底部为自由水面，顶部入渗率为0．002 cm／d。

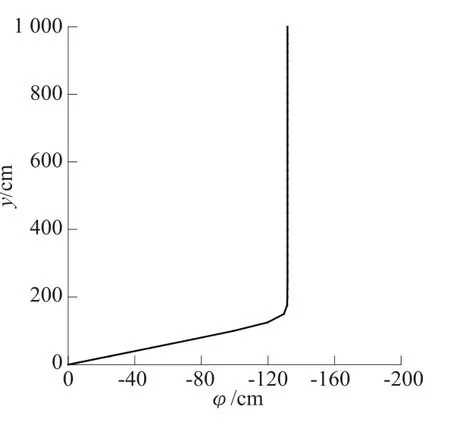
图6 负压水头均值Fig．6 Mean of negative pressure heads

图6 为负压水头均值分布图，在土柱底部由于毛细作用，负压水头均值近似呈斜线分布，到达一定高度后，负压水头均值为常数，此时非饱和渗流场的水力梯度为单位值1。图7所示为负压水头方差分布，由图可见，当 ln Ks和 α正相关时，负压水头的方差小于不相关时的方差值，这与已有的研究结果［5，12］是一致的。当ln Ks和α负相关时，负压水头的方差大于不相关时的方差值。从图6和图7可见，在土柱的较大区域内，负压水头的均值和方差都为常数，因而负压水头场在该区域内具有平稳性，可以用基于平稳谱理论的解析解对该平稳区内本文的数值结果作初步检验。平稳区的大小除了与土壤参数和边界条件有关外，还与土柱的高度有关。文献［13］的理论分析表明，ln Ks和α不相关和相关条件下的负压水头方差的比值可用下式计算：

图7 负压水头方差Fig．7 Variance of negative pressure heads

4 结 语

在水力特性参数空间变异性的影响下，渗流场具有一定程度的不确定性。本文分析了随机场KL展开的特点，阐述KL展开和摄动方法在渗流随机分析中应用的基本原理，分析表明利用随机场KL展开的均方收敛性和摄动方法的渐进收敛性，并将随机偏微分方程转化为递推的确定性偏微分方程组，提高了计算效率，这种分析方法可为类似问题的随机分析提供参考。对多参数随机场条件下非饱和渗流场进行随机数值模拟，考虑了参数随机场之间不相关、正相关和负相关3种情况，分析表明参数场之间的互相关性对渗流场的统计特征具有较大影响，在本文算例中得到的水头方差之间相差达几倍甚至几十倍。因此，必须进一步从理论和试验上探索岩土体渗流参数之间的统计相关特性，从而更好地分析渗流场的不确定性以及进行可靠性分析。

［1］ GRIFFITHSD V，FENTON GA．Seepage Beneath Water Retaining Structures Founded on Spatially Random Soil［J］．Geotechnique，1993，43（4）：577－587．

［2］ 李锦辉，王 媛，胡 强．三维稳定渗流的随机变分原理及有限元法［J］．工程力学，2006，23（6）：21－24．

［3］ 秦 权．随机有限元及其进展Ι．随机场的离散和反应矩的计算［J］．工程力学，1994，11（4）：1－10．

［4］ ZHANG D，LU Z．An Efficient，Higher－order Perturba－tion Approach for Flow in Randomly Heterogeneous Por－ous Media Via Karhunen－Loeve Decomposition［J］．J Comput Phys，2004，194（2）：773－794．

［5］ YANG J，ZHANG D，LU Z．Stochastic Analysis of Satu－rated－unsaturated Flow in Heterogeneous Media by Com－bining Karhunen－Loeve Expansion and Perturbation Meth－od［J］．JHydrol，2004，294：18－38．

［6］ GHANEM R，SPANOSP D．Stochastic Finite Elements：A Spectral Approach［M］．New York：Springer，1991．

［7］ PHOON K K，HUANG SP，QUEK ST．Implementation of Karhunen－Loeve Expansion for Simulation Using a Wavelet－Galerkin Scheme［J］．Probabilistic Engineering Mechanics，2002，17：293－303．

［8］ 曲延云，郑南宁，李翠华．Karhunen－Loeve展开基函数的小波分解算法［J］．自然科学进展，2005，15（3）：357－362．

［9］ 史良胜，杨金忠，李少龙，等．基于KL－Galerkin解法的地下水流动随机分析［J］．四川大学学报，2005，37（5）：31－35．

［10］史良胜，蔡树英，杨金忠．基于降雨空间变异的潜水运动随机模拟方法，Ι．非条件模拟［J］．水利学报，2007，38（4）：395－401．

［11］YEH T C J．One Dimensional Steady State Infiltration in Heterogeneous Soils［J］．Water Resources Research，1989，25（10）：2149－2158．

［12］李少龙，杨金忠，蔡树英．非饱和渗流随机模型中水力要素的随机特性研究［J］．岩土工程学报，2006，28（10）：1273－1276．

［13］YEH T C J，GELHAR L W，GUTJAHR A L．Stochastic Analysis of Unsaturated Flow in Heterogeneous Soils，2．Statistically Anisotropic Meida with Variable［J］．Water Resources Research，1985，21（4）：457－464．