地应力对洞室轴线布置影响的二维数值分析

王俊奇，颜月霞

（1.华北电力大学 可再生能源学院，北京 102206；2.石家庄铁道学院交通运输分院，石家庄 050043）

地应力对洞室轴线布置影响的二维数值分析

王俊奇1，颜月霞2

（1.华北电力大学 可再生能源学院，北京 102206；2.石家庄铁道学院交通运输分院，石家庄 050043）

深埋洞室处于高地应力条件下，水平应力常大于垂直应力，且水平方向应力也不均匀，洞室稳定性主要受初始应力场控制。采用可以施加轴向应力的二维非线性有限元方法，计算模拟并列双洞和单洞，研究自重应力场、最大主应力与洞线平行和垂直等三种应力场条件、两类岩石地下洞室轴线的选择对围岩变形及稳定的影响。结果显示，最大主应力与洞轴平行时，塑性区主要分布在边墙部位；最大主应力与洞轴垂直时，塑性区主要分布在洞室顶底部。《水工隧洞设计规范》中洞线宜与最大主应力方向一致的适用性是有条件的。

深埋洞室；变形与稳定；地应力；轴线布置；有限元法

1 概述

隧道轴线及大型地下洞室长轴轴线方位布置是地下结构设计的重要课题，深埋洞室高地应力条件下，初始地应力和洞室轴向布置的关系对洞室稳定有较大影响。相关规范及设计手册对此都有明确的原则性指示和规定［1～3］，认为“宜使洞线与最大水平地应力方向一致，或尽量减小其夹角”。有研究者持有与规范相同的观点［4～6］，且多是通过弹性力学解析结果来说明问题；也有在地应力场分析的基础上探讨地下洞室长轴向选取和地下厂房纵轴线方位的优化设计［7，8］，或探讨经典理论在较软弱围岩洞室受较大地应力影响所产生的强挤压问题［9］；更多的是通过二维或三维弹塑性有限元数值模拟研究具体工程开挖支护应力和位移，探讨地应力与洞室稳定的关系［10～16］，而系统研究地应力与洞室稳定关系的则较少。文献［17］通过采用边界元法研究矿井巷道，提出最大主应力理论，也有采用三维有限元分析深埋隧道［18］，得到一些一般结论。

综上，目前对深埋洞室轴线布置与洞室稳定关系的研究不足，本文采用可以施加轴向应力的二维非线性有限元方法，计算模拟并列双洞和单洞，系统研究不同初始应力场条件、不同性质岩石地下洞室轴线的选择对围岩变形及稳定的影响，探讨目前设计规范的适用性。

2 二维有限元研究对象及计算条件

2.1 研究对象

以均匀各向同性的Ⅱ级和Ⅲ级这两种代表性围岩为研究对象，不考虑地质结构面和岩体产状，分析各向同性均质岩体，采用Mohr-Coulomb屈服破坏准则。选取常见的圆拱直墙形状的洞室，研究两种情况：一类是两洞并列，模拟厂房等平行布置的洞群；一类为单洞，模拟输水隧洞或单独布置的厂房。考虑三类应力场，一类是自重应力场，另两类是铅直向为自重，水平最大主应力和最小主应力侧压力系数分别为1.4和0.6，洞轴与最大主应力平行和垂直的情况。

2.2 计算条件

2.2.1 有限元网格及边界条件

代表洞室宽8.0 m，高9.8 m，埋深400 m，为圆拱直墙式。计算两类洞室，一类为两洞并列，模拟洞群布置，间距20 m；另一类为单一洞室，计算时分别依照对称原则，取结构的一半进行分析。对于两洞情形，由于对称，结果中看似单洞，实为取其一半所致。约束条件，底部全约束，垂直边界法向约束。

2.2.2 计算工况

选择地下洞室围岩常见的Ⅱ级围岩和Ⅲ级围岩两种岩体材料，分别计算在自重应力场（水平方向均匀，且侧压力系数小于1）和水平方向为大小主应力作用方向，且有不同侧压力应力场条件下（铅直方向为自重），洞室开挖的稳定和位移情况。按照双洞和单洞，以及不同应力场进行组合，每一类型洞室有6种组合计算方案，见表1。

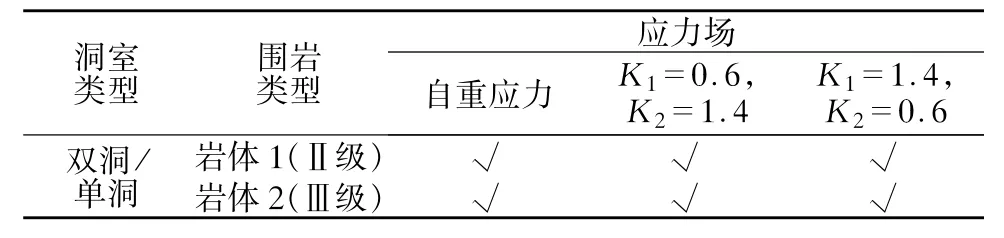
表1 计算方案Table 1 Computational schedule

2.2.3 材料参数

模拟洞室一次开挖，材料采用Mohr-Coulomb屈服准则，所选用的参数如表2所示，其中岩体1为Ⅱ级围岩，岩体2为Ⅲ级围岩［19，20］。

表2 材料参数Table 2 Mechanical parameters of rock

2.2.4 程序简介及计算结果说明［21］

数值分析所用程序为ABAQUS非线性有限元软件，其中有适于岩土工程问题的多个本构模型，如Mohr-Coulomb，Drucker-Prager，剑桥模型等。本文采用Mohr-Coulomb理想塑性屈服准则。

计算结果塑性区大小以等效塑性应变表示，其peeq定义为

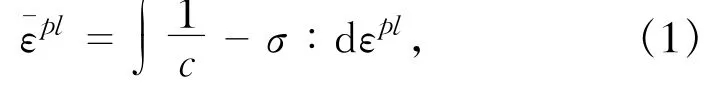
式中：¯εpl为等效塑性应变；σ为应力矢量；dεpl为塑性应变增量；c为粘聚力。

很多情况下，三维计算的代价和时间花费令人难以接受，需要简化为二维模型进行计算。普通二维有限元程序为平面应变程序，不能考虑隧道轴线方向地应力，本文所用程序不仅可以在平面上施加侧向压力，而且可以在与二维平面垂直的方向上施加轴向压力，实现类似三维计算所施加的轴向力，从而达到简化计算的目的。

3 轴向初应力施加原理

普通平面模型不仅要求计算平面是主平面，而且无法考虑垂直于计算平面方向上构造应力的作用。如何利用二维模型实现三维应力场模拟，是一个需要研究和探索的问题。美国垦务局发展了一种以平面模型解三维问题的方法［22］，这种方法的最大特点在于并没有假定垂直于计算平面方向的应力或应变为零，从而可以考虑岩体中存在的较大水平应力（地应力）对洞室岩体的影响。在有限单元法中，这种方法的关键在于建立岩体适当的应力应变关系或本构方程。

图1所示的平面单元，在单元的侧面上作用着水平构造应力或地应力，而其上的剪应力等于零，在这种情况下，单元中的应力状态是：

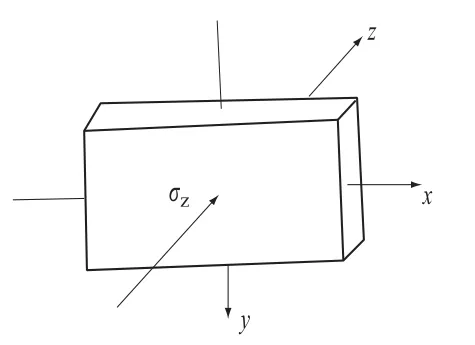
图1 具有轴向水平应力作用的平面单元Fig.1 Plane element with horizontal axis stress

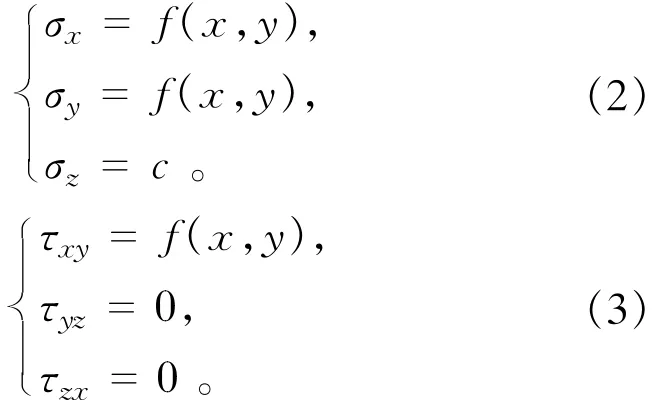
σx，σy及τxy是单元平面中的平面应力，σz是侧向水平应力，对于给定的单元来说，可以认为是常数，但是对于边坡模型中的不同单元来说，其值可以是变化的，以适应实际模型水平应力场的变化情况。

根据弹性理论，一般情况下单元的应力应变关系是：

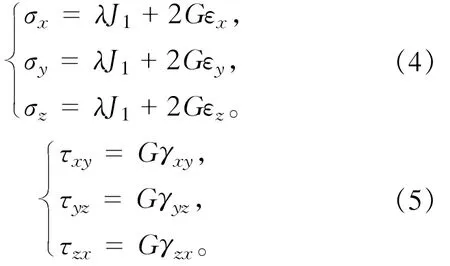
式中：J1为应变张量的第一不变量；λ为拉梅常数；G为剪切模量。因为在所示单元的情况下，σz=c，τyz及τzx均为零，从而得

这就是考虑水平构造应力或地应力作用时，用于有限元分析的物理方程。为了求解上述方程，还必须知道在单元中由于水平应力或地应力作用而产生的单元应力及单元的结点力。当单元的结点固定，也即不产生任何位移时，侧向均匀分别的水平应力σz在单元平面上便产生结点力。在这种情况下，因为εx，εy及γxy均为零，所以，仅考虑水平应力时，单元中的应力为

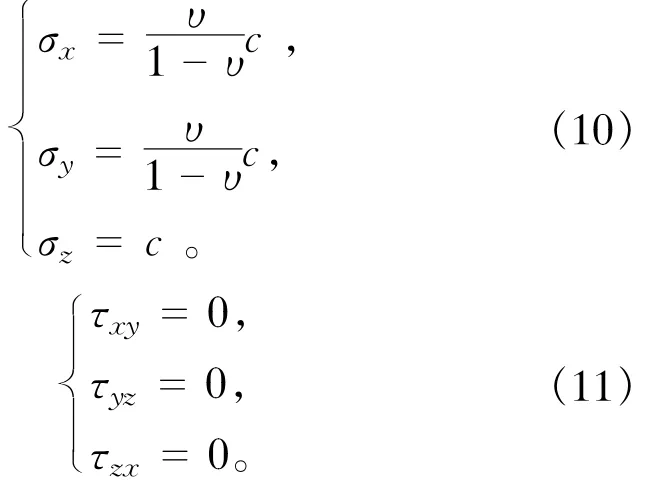
在上述应力的作用下，应用虚功原理，可将单元应力等效到结点上，得到单位厚度单元的结点力。

上述原理只是假定某一单元轴向应力一定，同时限定平面方向应变为零，从而得到仅有轴向应力时的单元应力。事实上，轴向应力是随着深度变化的，即公式（10）中的c是位置的函数，其大小根据设定的轴向压力系数确定。同时，x方向按照给定的侧压力系数设定，而y方向一般为自重应力，而不仅是公式（10）给出的轴向应力为常数情况，还需叠加与要求应力的差，也不会出现平面上的2个正应力总小于轴向应力情形。应用ABAQUS软件计算时，不必去关心其内核的处理，各方向应力只需给定压力系数即可实现相要求的应力，为了避免由于施加初应力产生的初始位移，需要注意初始应力场的平衡。

当然，虽然能够近似模拟三维效应，但总不能实现真三维有限元分析时轴向应力随开挖而变化的功能，也就是掌子面的空间效应无法在二维分析中体现，不过，这对分析洞室围岩整体稳定性影响不大。

4 有限元分析

4.1 双洞计算

4.1.1 塑性区

图2 Ⅱ级岩体等效塑性应变分布（等效塑性应变大于0.000 1）Fig.2 Distribution ofⅡgrade rock mass withεpl＞0.000 1

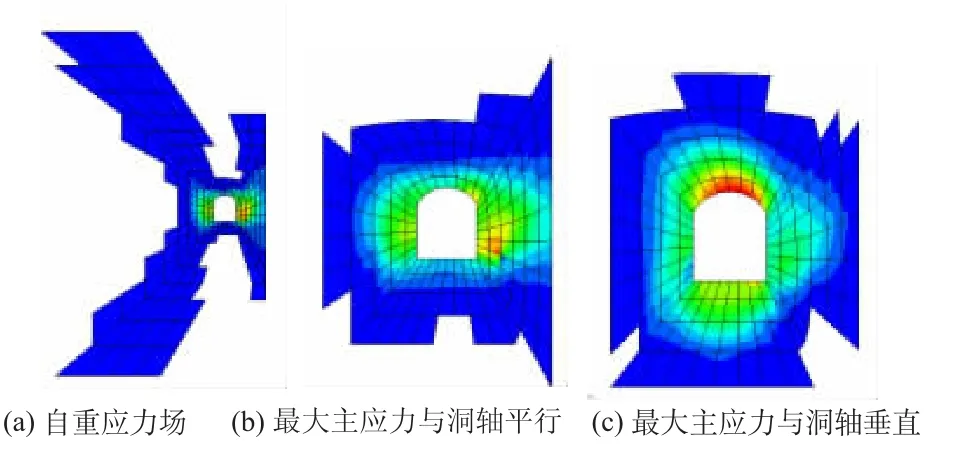
图3 Ⅲ级岩体等效塑性应变分布（等效塑性应变大于0.0001）Fig.3 Distribution of III grade rock mass withεpl＞0.000 1

在自重应力场，最大主应力与洞轴平行和最大主应力与洞轴垂直等3种条件下，洞室一次全部开挖后，塑性区分布（如图2和图3）分别对应质量等级为Ⅱ级和Ⅲ级的岩体，图中右侧是对称部分。以等效塑性应变大于0.000 1部分表示塑性区，网格多少反映塑性区范围大小，颜色深浅表示等效塑性应变数值大小。

由图2可见：Ⅱ级岩体，自重应力场条件下，塑性区主要分布在左右边墙，且向斜上方和下方延伸。最大主应力与洞轴平行时，塑性区分布在洞室四周，斜向部位屈服区减小，洞周塑性区分布均匀。最大主应力与洞轴垂直时，塑性区分布范围减小，主要分布在底板、拱顶，边墙部位明显减小。由图3可见，Ⅲ级岩体，自重应力场条件下，塑性区分布在边墙和拱顶，且在四角斜向45°方向延伸范围较大，右边墙双洞并列部位连为一体。最大主应力与洞轴平行，顶底部塑性区范围增大，边墙部位斜向延伸区域减小，塑性分布区在洞室周围较均匀。最大主应力与洞轴垂直，洞室顶底部塑性区范围继续增大，侧墙部位减小。

4.1.2 位移

洞周各部位位移最大处上下左右分别对应的弹塑性总位移和塑性位移占全部位移比例见表3。

Ⅱ级围岩，自重应力场条件下，左右边墙主要为塑性位移。最大主应力与洞轴平行条件下，塑性位移在左右边墙的比例比拱顶和底板的比例大。最大主应力与洞轴垂直条件下，塑性位移性质与最大主应力和洞轴平行情况相反。上述3种条件下收敛变形趋势为：水平和竖直方向都有所增大，但水平方向由塑性位移为主，转为以弹性位移为主。

材料力学参数下降后，为Ⅲ级围岩时，应力场条件依次为自重应力场、最大主应力与洞轴平行和垂直，塑性区范围在侧墙部位减小，在洞室顶部和底部增大。收敛位移主要是塑性位移，水平方向，洞轴与大主应力平行时最大，垂直时最小；竖直方向，洞轴与大主应力垂直时最大，比平行时增大近一倍。

岩体相对变弱，为Ⅲ级围岩时，洞轴与最大地应力平行时，洞室水平方向收敛变形是竖直方向的两倍；洞轴与最大地应力垂直时，洞室竖直方向收敛变形略大于水平方向，可称为应力变形的正交性［10］。

4.2 单洞计算

4.2.1 塑性区

自重应力场条件，以及最大主应力与洞轴平行和最大主应力与洞轴垂直时，洞室一次全部开挖后，塑性区分布如图4和图5，分别对应质量等级为Ⅱ级和Ⅲ级的岩体。

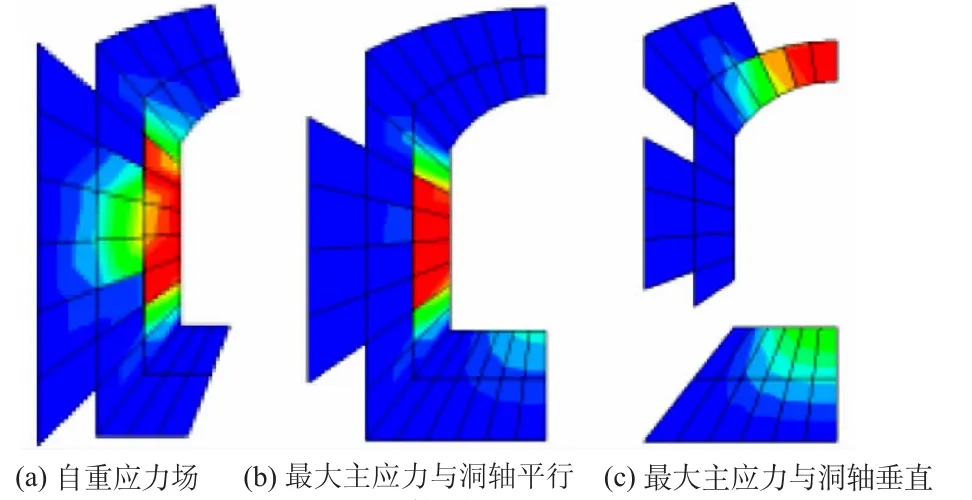
图4 Ⅱ级岩体等效塑性应变分布（等效塑性应变大于0.000 1）Fig.4 Distribution ofⅡgrade rock mass withεpl＞0.000 1

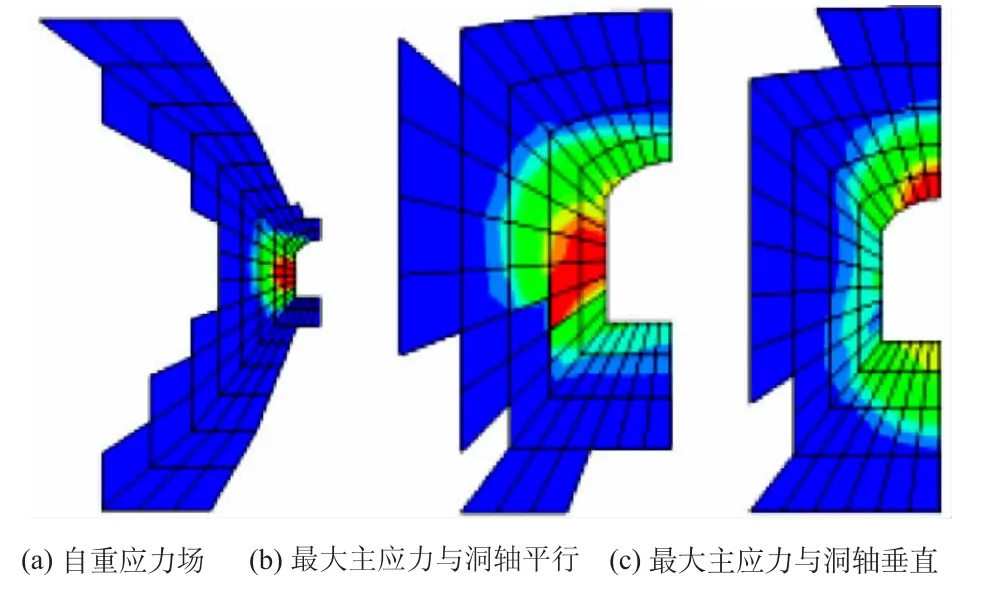
图5 Ⅲ级岩体等效塑性应变分布（等效塑性应变大于0.000 1）Fig.5 Distribution ofⅢgrade rock mass with εpl＞0.000 1

Ⅱ级岩体，自重应力场条件下，塑性区主要分布在边墙。最大主应力与洞轴平行时，塑性区范围减小，在洞周均匀分布。最大主应力与洞轴垂直时，塑性区主要分布在底板和顶部，边墙部位屈服程度减弱。

Ⅲ级岩体，自重应力场条件下，塑性区分布在边墙及其上方和下方斜向45°延伸。最大主应力与洞轴平行，顶部和底部塑性区范围增大，斜向部位减小。最大主应力与洞轴垂直，洞室顶部和底部塑性区范围继续增大，边墙部位明显减小。

4.2.2 位移

洞周各部位上下左位移最大处分别对应的弹塑性总位移和塑性位移占全部位移比例见表4。

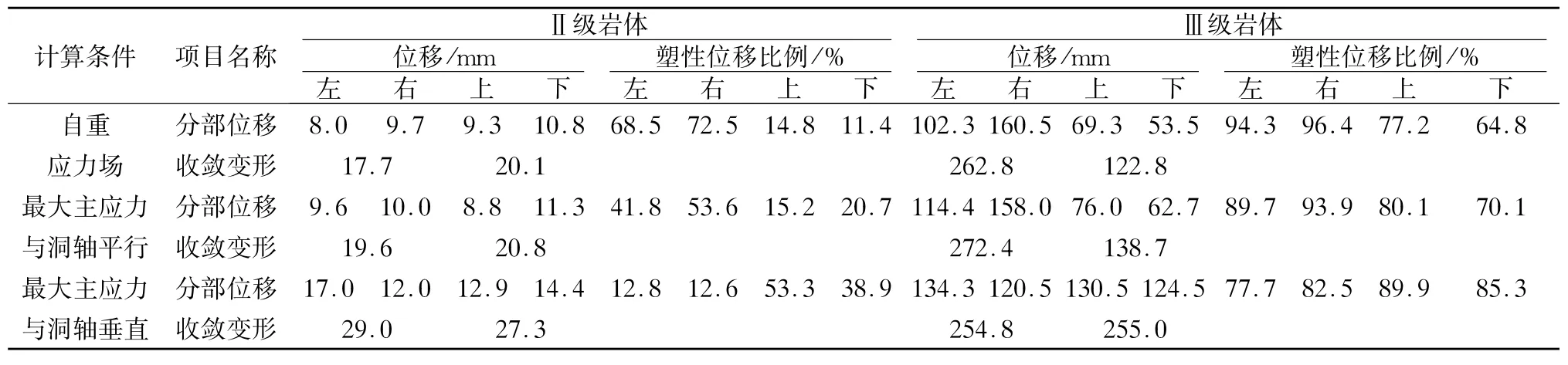
表3 双洞计算位移结果比较Table 3 Comparison of displacements of two parallel tunnels

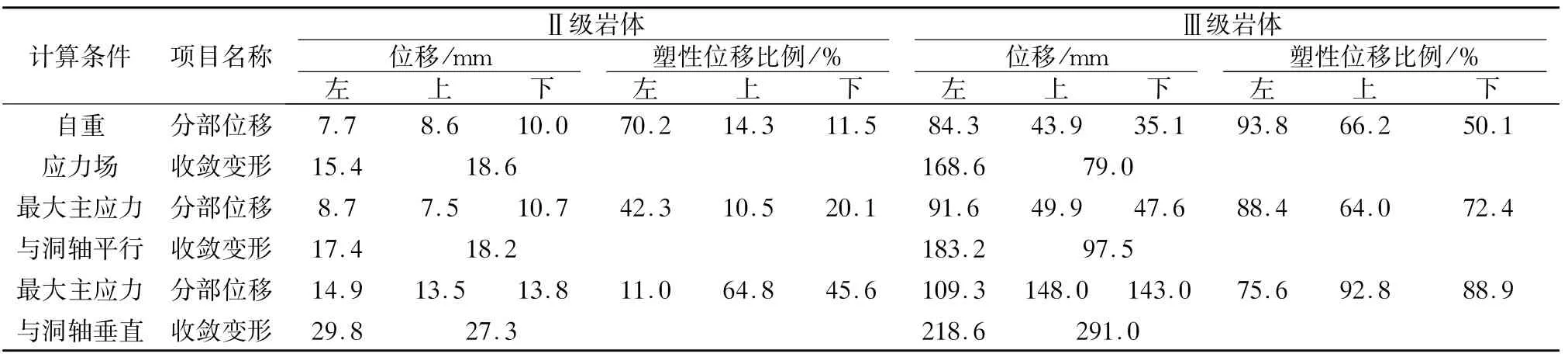
表4 单洞计算位移结果比较Table 4 Comparison of displacements of single tunnel

Ⅱ级围岩，自重应力场条件下及最大主应力与洞轴平行和垂直条件下，塑性位移比例由边墙为主转为以洞室顶底部为主，最大主应力与洞轴垂直时，位移较前两应力场增大。

Ⅲ级围岩，材料力学参数下降后，三应力场条件下，收敛位移，水平方向弹性位移增加，总位移增加，分别为168.6，183.2，218.6 mm。竖直方向塑性位移增大明显，总变形依次为79.0，97.5，291.0 mm。岩体变弱，与双洞相似，也表现出应力变形的正交性。

4.3 洞间距影响

本次计算只选取了洞间距20 m一种条件，比较图2和图4，对于Ⅱ级围岩，若将图2中的洞室右半部切去，塑性区跟图4分布相似，范围相差不多。说明此时洞间距影响不显著。

比较图3和图5，对于Ⅲ级围岩，塑性区发展规律类似，但若将图3中的洞室右半部切去，同样取值界限塑性区要比图5分布范围大些，这是由于岩性变弱，故显示出双洞对于塑性区发展的影响。

5 计算结果解释

在一定的初始应力场条件下开挖洞室，由于开挖后洞室内部出现临空面，开挖前后应力差组合，与普通不能施加轴向力的平面应变程序的分析结果有很大的不同，得到的岩体塑性屈服区与平面应变计算结果也不相同，可施加轴向力的二维分析更能真实反映岩体屈服与位移情况。

5.1 塑性区分析

在进行洞室开挖时，根据出现临空面的位置和所处的应力状态，二维模型，容易进入塑性区的部位分别是边墙、顶拱和底板。在临空面附近取微单元，开挖前，3个主应力为 K1σz，σz，K2σz，其中 K1＞K2，σz为铅直方向自重应力。对于自重应力场，σ1=σz，水平方向侧压力系数K1=K2=K＜1。洞室开挖后，临空面方向微单元的主应力近似为零，据此将开挖前后洞室的应力场和屈服情况做一总结分析，自重应力场条件见表5，其他条件如表6分析。

自重应力场条件下，开挖后边墙和端墙主应力差为σz，而顶底板为Kσz，侧压力系数K＜1，则边墙部位开挖临空范围大，屈服最严重，顶底板屈服区稍小。

最大主应力与洞轴平行，开挖后，边墙和顶底板主应力差均为K1σz，洞室周围屈服程度应基本一致。

表5 自重应力场条件下开挖前后屈服分析Table 5 Analysis under the gravity stress condition

表6 水平方向为主应力场条件下开挖前后屈服分析Table 6 Analysis under the horizontal stress condition

最大主应力与洞轴垂直时，边墙主应力差为σz，顶底板和端墙为K1σz，由于K1＞1，则顶底板屈服严重边墙部位减弱，这与计算结果一致（见图2至图5）。

5.2 位移分析

自重应力场时，水平方向应力均匀，不影响洞线选择，这里主要比较水平应力场情况。

由上节的表3和表4，Ⅱ级围岩，变形主要为弹性，最大主应力与洞轴平行时，竖向收敛变形大于水平方向，相差不大。最大主应力与洞轴垂直时，水平方向收敛变形大于竖向。

Ⅲ级围岩，主要为塑性变形，最大主应力与洞轴平行时，水平方向收敛变形大于竖向。最大主应力与洞轴垂直时，竖向收敛变形大于水平方向。

岩性较好时，变形与主应力方向一致，当岩性较差时，洞室位移主要是塑性位移，因而表现出应力位移正交性现象。

6 结论和建议

采用可施加轴向力的二维非线性有限元方法，就隧道轴线、大型地下洞室长轴轴线布置与初始地应力场关系对洞室稳定影响这一课题进行研究，揭示出一些新认识，与规范建议的原则“考虑地应力对围岩稳定的影响，在高应力区隧洞轴线方向宜与最大水平地应力方向一致，或有较小夹角”不完全吻合。可以得到以下几点初步结论：

（1）洞室轴线与最大水平地应力平行，洞室顶底板塑性区较小，边墙部位塑性区较大，洞线与最大水平地应力垂直，塑性区在顶底板范围增大，边墙部位减小。岩性下降，Ⅱ级到Ⅲ级围岩，塑性区范围扩大。

（2）岩性较好时，Ⅱ级围岩变形主要为弹性，最大主应力与洞轴平行时，竖向收敛变形大于水平方向，但相差不大。最大主应力与洞轴垂直时，水平方向收敛变形大于竖向。

（3）岩性较差时，Ⅲ级围岩变形主要为塑性变形，最大主应力与洞轴平行时，水平方向收敛变形大于竖向。最大主应力与洞轴垂直时，竖向收敛变形大于水平方向，有大主应力和位移正交性现象。

按照所得的塑性区分布和位移结果，就所讨论的圆拱直墙式洞室，可有以下建议：

（1）岩性较好时，位移主要为弹性，且数值较小，因此只将塑性区分布规律作为选线标准。为增大洞室顶底板稳定性，宜将洞轴与最大水平地应力平行布置，为增大洞室边墙稳定性，宜将洞轴与最大水平地应力方向大角度相交。

（2）岩性较差时，仅考虑塑性区分布，仍有以上建议。但由于应力位移有正交现象，洞轴与大主应力垂直时，竖直方向收敛变形增大较多。为控制位移，可依照规范建议洞线与大主应力平行布置，但边墙部位如有不利的地质构造，其危险性将加大。

（3）所得塑性区分布规律可作为设计和施工中喷锚支护的参考，比如锚杆布置的范围和长度等。工程实践中，应综合考虑地质构造因素和地应力影响分析结果，结合经验做出决策。规范原则性的指示和规定并不总是有利的，有一定的适应条件，需要根据具体问题灵活掌握应用。

［1］ SL279-2002，水工隧洞设计规范［S］.

［2］ DL／T5195-2004，水工隧洞设计规范［S］.

［3］ 水利水电规划设计总院，水利水电地下建筑物情报网.水利水电工程地下建筑物设计手册［M］.成都：四川科学技术出版社，1993.

［4］ 段乐斋，杨欣先，夏广逊，等.水工隧洞和调压室（水工隧洞部分）［M］.北京：水利电力出版社，1990.

［5］ 谷兆祺，彭守拙，李仲奎.地下洞室工程［M］.北京：清华大学出版社，1994.

［6］ 范秋雁.选择巷道合理开挖方向的力学分析［J］.煤炭学报，1990，15（3）：62-70.

［7］ 戚 蓝，马启超.在地应力场分析的基础上探讨地下洞室长轴向选取和围岩稳定性［J］.岩石力学与工程学报，2000，19（增刊1）：1120-1123.

［8］ 李 莉，何江达，余 挺，等.关于地下厂房纵轴线方位的优化设计［J］.四川大学学报（工程科学），2003，35（3）：35-37.

［9］ 符华兴.强挤压地下洞室的塑性形变压力问题及其工程措施［J］.铁道工程学报，2004，（4）：82-84.

［10］张志强，郑鸿泰.圆形隧道应力-应变正交关系的力学行为研究［J］.岩石力学与工程学报，2000，19（增刊1）：840-844.

［11］张志强，郑鸿泰.高地应力条件下隧道大变形的数值模拟分析［J］.岩石力学与工程学报，2000，19（增刊1）：957-960.

［12］邵国建.初始地应力场对洞室围岩稳定性的影响［J］.水文地质工程地质，2003，6（30）：44-48.

［13］靳晓光，李晓红，艾吉人，等.某深埋长隧地应力演化及围岩应力位移模拟研究［J］.水文地质工程地质，2004，31（1）：40-43.

［14］孙红月，尚岳全，张春生.大型地下洞室围岩稳定性数值模拟分析［J］.浙江大学学报（工学版），2004，38（1）：70-73.

［15］陈方方，李 宁，张志强，等.高地应力区隧洞稳定性的数值仿真分析［J］.水利与建筑工程学报，2004，2（1）：47-50.

［16］朱以文，黄克戬，李 伟.地应力对地下洞室开挖的塑性区影响研究［J］.岩石力学与工程学报，2004，23（8）：1344-1348.

［17］GALE W J，BLADKWOOD R L.Stress Distribution and Rock Failure Around Coal Mine Roadways［J］.Int J Rock Mech Min Sci&Geomech Abstr，1987，24（3）：165-173.

［18］ABDEL-MEGUID M，ROWE R K，L0 K Y.Three-dimensional Analysis of Unlined Tunnels in Rock Subjected to High Horizontal Stress［J］.Can.Geotech.J.2003，40：1208-1224.

［19］GB50218-94，工程岩体分级标准［S］.

［20］关宝树.隧道工程设计要点集［M］.北京：人民交通出版社，2003.

［21］庄 茁，张 帆，岑 松，等.ABAQUS非线性有限元分析与实例［M］.北京：科学出版社，2005.

［22］刘汉东，张 勇，贾金禄.岩土工程数值计算方法［M］.郑州：黄河水利版社，1995.

2-D Numerical Analysis on Influence of In-situ Stress on Tunnel Axis Orientation

WANG Jun-qi1，YAN Yue-xia2

（1.School of Renewable Energy Resources，North China Electric Power University，Beijing 102206，China；2.School of Transportation Engineering，Shijiazhuang Railway Institute，Shijiazhuang 050043，China）

Deeply buried tunnels usually lie in high stress fields，in which horizontal stresses are not uniform and far larger than vertical stresses，and tunnel stability is dominated by the original in-situ stresses.With three-dimensional nonlinear finite element method，the effects of tunnel in axis orientation on the displacement and stability of two types of surrounding rocks are studied systematically for two parallel tunnels and single tunnel.The tunnel lies in different kinds of rocks and in such different original stress fields that the maximum horizontal principal stress is parallel to or perpendicular to the axis or the stress field is gravity.The numerical analysis results show that the plastic zones occur in the side wall of the tunnel mostly when the horizontal maximum principal stress is parallel to the tunnel axis，while the plastic zones distribute in the top and bottom of the tunnel when the horizontal maximum principal stress is perpendicular to the tunnel axis.It is concluded that the instruction of tunnel axis should be parallel to horizontal maximum principal stress regulated by the“specification for design of hydraulic tunnel”is not available for the stability of tunnel always.

deeply buried tunnel；deformation and stability；in-situ stress；tunnel axis orientation；finite element method

P642

A

1001-5485（2009）07-0033-07

2008-12-27；

2009-02-13

中国水利水电科学研究院青年科学基金资助项目（04QN03）

王俊奇（1971-），男，山西朔州人，副教授，博士，从事水工结构、岩土工程研究，（电话）15801452959（电子信箱）jqwangmail＠163.com。

（编辑：刘运飞）