小学数学中上位观念教学探析

　　新课程改革下，小学数学课程标准安排了数与代数、空间与图形、统计与概率、实践与综合应用四个学习领域。课程内容的学习，强调学生的数学活动，发展学生的数感、符号感、空间观念、统计观念，以及应用意识与推理能力。但大部分学生在学习中都是把这四部分肢解开来分散学习，同样教师在教学和教材的呈现上也是把每部分各自独立的讲解给学生。这样做的后果是学生接触的总是零碎的各种知识点，缺乏触类旁通与整合的能力，学生的学习被捆绑在不断接受和记忆新的知识点上，不能做到对知识的融会贯通，在激发智慧、培育创造灵感等方面的效果更不明显。在学习和保持时，往往机械地记忆学习材料，以达到考试的目的。学生常常会体验到不必要的困难，而很少有成功的机会。那么怎样做才能减轻学生的学习负担，让他们真正的运用已有的数学观念去主动学习呢？
　　
　　一、上位学习概念的引入
　　
　　奥苏贝尔的学习理论提供了解决的办法，他根据将要学习的新内容与学习者已经知道的相关内容之间的关系，把学习分为下位学习、上位学习、并列结合学习。
　　如果将要学习的新内容在包摄和概括水平上低于学习者原有认知结构中已有的相关内容，这时的学习就是下位学习或类属学习。
　　如果将要学习的新内容在包摄和概括水平上高于学习者原有认知结构中已有的相关内容，这时的学习就是上位学习或总括学习。
　　如果将要学习的新内容不能与认知结构中某些特定的内容构成下位关系（从属关系）或上位关系（总括关系），那么，这时的学习就是并列结合学习。这种学习和记忆都比较困难。
　　认知结构的层次组织是按包容性逐渐下降的方式进行的，而且这种学习具有通过一个使未分化的领域逐渐分化获得增长的机制。但现在的小学数学教学却是习惯把某些数学观念或课题肢解在相应的章节里而相互隔离。要求学生在习得一定数量并处于适当概括水平的相关的起归属作用的观念以前，先学习新的和不熟悉的那些知识细节，导致了上面学习现象的发生。所以，在教学中应尝试遵照奥苏贝尔的学习理论，在学习知识点的同时，适当渗透可以连接各领域学习内容的上位数学观念。当学生初步形成这些上位数学观念时，再逐步把零散的知识点归属到这些上位观念之下，从而产生最优的学习效果。
　　
　　二、在教学中渗透上位观念学习的效果研究
　　
　　下面就以实际教学为例研究一下在数学教学中渗透上位数学观念的效果。
　　1.“转化”思想在教学中的应用
　　“转化”思想是研究和解决数学问题的一种有效的思考方法，是运用事物运动、变化、发展和事物之间互相联系的观点，把未知变为已知，把复杂变为简单的思维方法。在小学数学的教学中如果教师能在教学中结合具体的教学内容，渗透数学“转化”思想，有意识地培养学生运用“转化”思想解决问题，就可以让学生找到不同类知识学习上的共同之处，触类旁通，从而大大提高教学效果。
　　例如，笔者在五年级“除数是小数的除法”的运算教学过程中这样提问：你会解答什么样的除法算式？我们怎样把小数除法转化成整数除法进行计算呢？看完下面的习题后，请进行思考。
　　(1)填写并思考各式之间有什么规律，运用了什么运算性质。
　　62/2=（ ）；620/20=（ ）；6200/200=（ ）；
　　(2)在括号里填上合适的数，除数必须是整数，商不变。
　　3.2/0.4=（ ）/（ ）；3.6/0.006=（ ）/（ ）；
　　42/0.105=（ ）/（ ）；1.125/0.45=（ ）/（ ）。
　　通过这组习题，重温了“商不变”的性质，让学生明了转化法的应用，鼓励学生实现了除数由小数到整数的转化，学生在充分感知中明确了算理，在探索中逐步掌握了算法，同时加深了对转化观念应用的认识。在数的运算中，都是把小数乘法、除法转化成整数乘法，分数除法转化成分数乘法等；同时在几何知识中，也是把平面图形的面积公式与立体图形的体积公式等的推导转化成已学过的图形进行。教师如果通过数学不断地让学生了解、认识数学的转化方法，逐步渗透转化意识，当学生认识转化观念以后，在学习其它的知识时，只要稍加点拨，学生就能运用这种观念自主的学习。
　　在学习完运算这一单元后，紧接着学习长方体、正方体的体积计算。笔者让学生计算一个不规则的铁块的体积，学生们顿时议论纷纷，认为不可能计算，因为无法计量它的长、宽、高。但当笔者在黑板上写出“转化”两个字后，不久就有学生提出，可以把它转化为标准的长方体，然后再进行计量与计算。可是怎么转化呢？通过小组讨论后，学生们的答案可谓精彩纷呈。
　　小组一：可以请铁匠师傅帮个忙，让他敲打成一个规则的长方体后再计算。
　　小组二：可以用一块橡皮泥，根据铁块的形状，捏成一个和它体积一样的模型，然后把橡皮泥捏成长方体或正方体。
　　小组三：用钢锯把它锯成一个规则的长方体，然后把铁屑压在一个长方体的模具中进行计量，最后把两个体积相加。
　　小组四：把这个铁块扔到一个装有水的长方体的水槽内，看看水面上升了多少，拿水槽内底面的长、宽与水面上升的高度相乘得到铁块的体积。
　　小组五：还有更简单的，就是把铁块放到一个装满水的量杯内，使之淹没，然后拿出来，看看水少了多少毫升，这个铁块的体积就是多少立方厘米。
　　这两个课例表明，正是由于学生在运算教学中认识到了“转化”这一上位数学观才能在空间与图形学习中主动参与，从自身知识基础与经验出发，把新知转化成旧知，建立新旧知识的内在联系，促进新知识结构的建立，进而主动地理解和掌握转化的方法，提高学生自主学习的能力。
　　2.类比观念在教学中的应用
　　类比就是根据两个对象之间在某些方面的相同或相似，推出它们在其它方面也可能相同或相似的一种推理方法。类比的观念在小学数学教学中的应用也很广范，教师在教学过程中如果适当地培养学生运用类比法进行合情推理的能力，就可以促进学生思维的变通，提高其思维的创造性。
　　例如，低中年级应用题中经常出现“松树比杨树少15棵”类型的题目，学生对其中的“相比较的两个量谁多谁少？”这个问题的回答往往是“杨树少，松树多”，尽管教师多次提醒学生要认真看清题目，但学生还是“不听话”，其实学生对这句话没有理解。可以用类比法进行引导，效果会很好。问：“小龙，你几岁了？”（9岁），“你妈妈今年多大了？”（33岁），“那么，能不能根据谁比谁少说一句话？”答：“小龙的岁数比妈妈少24岁”。问：“同样的，松树比杨树少15棵，是谁多谁少？”这样的类比设问，学生学得既有趣又掌握得好。这种类比的观念不仅在应用题教学中能得到应用，在空间与图形知识的学习中也能起到很大的作用。
　　在教学“圆的周长”时，学生已有长方形和正方形周长的基础，引导学生通过比较，得出它们的共同点：都是封闭的平面图形，它们的周长都与图形中的某些线段有关。那么圆的周长呢？让学生大胆猜测，圆的周长是否也和其中的某条线段有关呢？再让学生动手实践，用绳测法、滚动法等多种方法测量出课前准备好的圆形物体的周长，对测量出的数据进行归类整理成下表。
　　
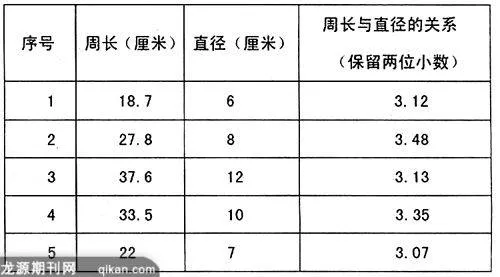
　　通过表格中的数据，学生很容易看出：圆的周长总是直径的3倍多一些。实际上，任何圆的周长和直径的比值都是一个固定的数，我们把它叫做圆周率，于是得到圆周长的计算公式：
　　圆的周长=圆周率×直径
　　同样类比的观念在学习其它知识上也有其独到的应用，“比和比值”的教学中，从两个同类量之间的相除关系、不同类量之间的相除关系扩展到两个一般数量之间的相除关系，引导概括出“两个数相除，又叫做两个数的比”。在除法的旧知识结构上寻找比的知识生长点，再通过与分数之间的对比，从而在比、除法和分数之间建立起牢固的联系。为加深理解，可设计对比性的巩固练习，从而建立起知识网络。
　　不难看出，对学生而言，如果对类比的观念有所领悟，就能把知识化难为易，激起探索的兴趣。类比的观念不仅使数学知识容易理解，而且使公式的记忆变得自然和简洁，从而激发学生的创造力。有意识地、合理地运用类比法，学生可以在问题质疑和研究过程中，体验到“真正的创新”所带来的愉悦，这是创新精神的“源动力”。
　　“转化”和“类比”只是小学数学中运用比较广泛的两个数学观念，在小学数学教学中经常运用到的上位数学观念还有统一的数学观念、假设求证的数学观念、按区间分类的数学观念、极限的数学观念等等。虽然这些观念不能作为知识目标直接讲给学生，但是如果教师在教学过程中注意渗透这些观念就可以帮助学生在这些上位观念的指导下建立不同知识之间的联系，自主地、创造性地学习，真正做到“授人以渔”。
　　
　　三、在数学教学中渗透上位观念学习的局限
　　
　　虽然在小学数学教学中适当的渗透上位数学观念可以解决学生把知识点割裂开、被动接受知识的问题，但在具体的教学过程中还存在着一定的局限性。
　　一是上位观念学习效果的迟效性。由于教材的呈现方式是按知识领域把知识点分成若干个单元，所以当学生认识到一些数学观念以后，教师无法做到让学生马上运用这种观念去学习相联系的知识，同时学生也不容易马上体验到在上位观念指导下学习的顺利，使教师无法对上位观念学习的效果进行评价。
　　二是上位观念渗透的无标准性。虽然大家都承认小学数学教学中可以渗透很多数学观念，但这些数学观念的渗透大都是一线教师通过自己的经验总结而成的。而指导小学数学学习的上位观念都有哪些，在哪些知识点上可以用到这些观念却没有权威性的标准。这就使教师只能用自己的经验来对学生进行渗透，而无法把这些观念的学习融入到教学目标中去。
　　总之，在小学数学中融入上位观念的教学，一方面可以把零散的知识点归属到这些上位观念之下从而让学生产生最优的学习效果；另一方面可以把学生从不断地接受和记忆新的知识点的捆绑中解脱出来，从而减轻学生的学习负担，让他们真正的运用已有的数学观念创造性地主动学习。但是实际教学中上位观念的教学还存在一定的局限性，这种教学方式还需要不断的探索和完善，当这种教学方式成熟后或许会成为小学数学课程改革的一条新路。
　　（作者单位：北京市大兴区黄村镇第一中心小学）