基于轨迹线性化方法的近空间飞行器鲁棒自适应控制*

2008-12-12敬忠良胡士强

空间控制技术与应用 2008年1期

关键词：适应控制鲁棒线性化

敬忠良，朱亮，陆平，胡士强

（上海交通大学空天科学技术研究院，上海200240）

基于轨迹线性化方法的近空间飞行器鲁棒自适应控制*

敬忠良，朱亮，陆平，胡士强

（上海交通大学空天科学技术研究院，上海200240）

研究一种新的近空间飞行器鲁棒自适应飞行控制系统设计方案。利用单隐层神经网络的函数逼近能力和被控对象分析模型的有用信息构建一种单隐层神经网络干扰观测器，用以在线估计系统中存在的不确定性，具有自适应调节能力的鲁棒控制器用以克服估计误差。将所得单隐层神经网络干扰观测器与轨迹线性化方法结合形成新的非线性系统鲁棒自适应控制方案，严格的理论证明在给定的自适应调节律作用下闭环系统所有误差最终有界。该控制方案被用于近空间飞行器飞行控制系统设计，高超声速飞行条件下的仿真结果表明该方法不仅有效，而且能够提供高精度、高稳定度的控制性能。

飞行控制；非线性控制；鲁棒自适应控制；高超声速飞行器

1 引言

近空间飞行器（Near Space Vehicle，NSV）是指运行在距地面30-70km空域范围内的飞行器，自美军在“施里弗-3”空间作战军事演习中首次将近空间纳入作战视野以来，NSV重要的军事应用价值引起世界各国的广泛关注[l]。

NSV的一种飞行方式是在近空间做高超声速飞行，突出的快速响应能力和突防能力使其具有极高的应用价值，但高超声速飞行作为一种极端的飞行状态，导致NSV在飞行过程中呈现激烈快时变、严重非线性、强耦合、不确定等特点，因而给控制系统设计带来极大挑战[2]。自适应轨迹线性化控制（Adaptive Trajectory Linearization Control，ATLC）方法是一种近年来刚刚兴起的非线性控制系统设计方法，它在原有TLC控制方法的基础上通过引入补偿控制律抵消系统中存在的建模误差、外界干扰等不确定因素对系统性能的影响，克服TLC方法鲁棒性不足的缺点，从而获得满意的控制性能。文献[3]基于单隐层神经网络（Single Hidden Layer Neural Networks，SHLNN），研究一种直接自适应TLC控制方法，该方法的不足在于构造自适应控制律时，忽略许多被控对象分析模型中的有用信息。文献[4]提出一种基于径向基神经网络干扰观测器（Radial Basis Function Neural Network Disturbance Observer，RDO）的自适应TLC方法。该方法在实现时充分利用了径向基神经网络的逼近能力以及被控对象分析模型提供的有用信息，因此可以对系统中存在的不确定性做出更好的估计。但它的不足在于需要事先正确选择径向基神经网络的高斯函数中心和宽度，否则将影响径向基神经网络的逼近能力，进而影响整个控制系统的性能。

本文首先采用SHLNN技术推广了文献[4]中的RDO设计思想，由于SHLNN属于一种非线性参数的估计器，可以避免类似RDO需要选择高斯函数中心和宽度所带来的问题。此外，考虑到文献[3，4]采用的具有固定增益的鲁棒控制器，设计保守性大且容易引起系统振荡的问题，本文设计了具有自适应调节能力的鲁棒控制器，通过将所得的单隐层神经网络干扰观测器（SDO）技术与TLC方法结合，获得一种新的非线性系统鲁棒自适应控制方法并用于NSV飞行控制系统设计，仿真验证表明该方法不仅有效，而且能够提供高精度、高稳定度的控制性能。

2 问题陈述

不失一般性，本文考虑如下不确定非线性系统：

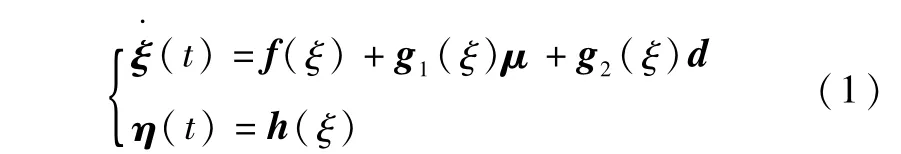
其中 ξ∈Rn表示系统状态，μ∈Rm表示控制输入，f∈Rn，gl、g2∈Rn×m，h∈Rm光滑有界，d∈Rm表示未知的建模误差和外界干扰等不确定性，并假设在ξ定义域上，存在范数有界的非奇异矩阵g0（ξ）∈Rm×m使得下式成立：

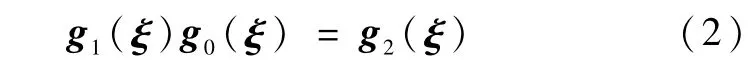
根据TLC方法的设计原理[5]，首先令和为满足系统（l）中分析模型的标称状态、输入和输出，即：

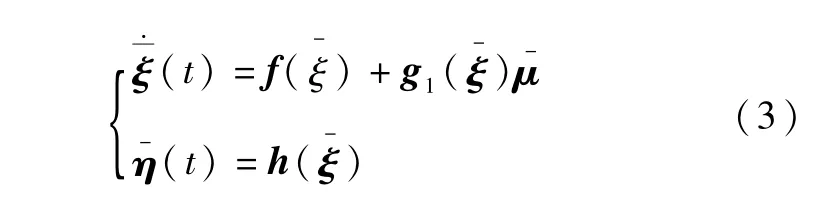
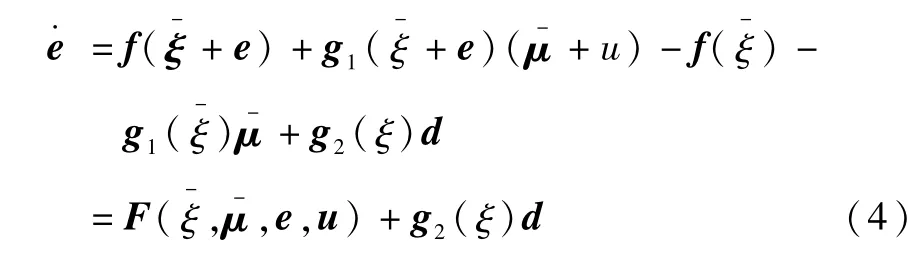
那么原有的轨迹跟踪问题转化为误差调节问题，此时控制系统实现的关键在于根据系统误差状态e设计合适的反馈调节器u来镇定系统（4）并使整个系统具有期望的响应特性。由于不确定性d存在，整个闭环系统还应具有一定干扰衰减能力。虽然从理论上讲，当式（4）中无扰系统u）全局指数稳定时，系统对不确定性d具有最大鲁棒性，但考虑到实现的可行性，TLC方法采取将在平衡点e=0附近线性化，然后利用线性时变系统的相关理论实现u。具体实现时由于可视为式（4）中已知的时变参数，u为跟踪误差e的函数，因此简记式（4）为

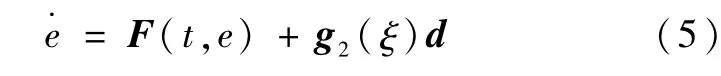
假设1e=0为=F（t，e）的孤立平衡点，F：[0，∞]×De→Rn，De=｛e∈Rn|‖e‖＜Re｝连续可微，Jacobian阵[∂F/∂e]关于t一致有界，在De上满足Lipschitz条件，‖·‖表示Frobenius范数。

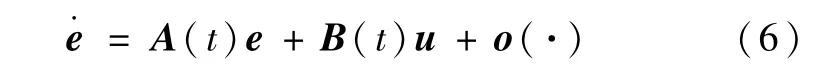
式中 o（·）为线性化余项，满足‖o（·）‖≤l‖e‖2，l表示Lipschitz常数，A（t）、B（t）如文献[3]中式（5）所示，均为线性时变矩阵。

假设2矩阵A（t）、B（t）对所有允许的参数值满足：（ⅰ）关于t光滑有界且有连续有界的n-l次微分；（ⅱ）rank[B（t）]≡m；（ⅲ）｛A（t），B（t）｝一致完全能控。

若式（5）满足假设l和假设2，那么存在LTV反馈控制律u=K（t）e使得

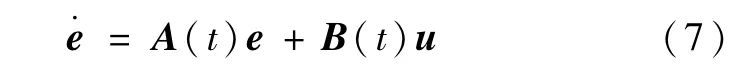
在原点指数稳定[7]。不妨记

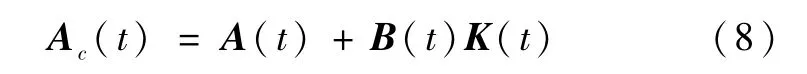
值得注意的是，这种线性化的处理方式虽使设计难度降低，但局部指数稳定无法提供足够的干扰衰减能力和鲁棒特性，特别对于NSV这种难以精确建模且运行环境十分恶劣的控制对象来说，‖d‖很有可能超过TLC方法提供的稳定裕量，使整个系统面临失效，文献[3，4]从理论分析和仿真验证都已表明这一点。因此目前有关TLC方法理论研究的一个方向是如何扩大TLC方法的稳定裕度，使其具有更强的鲁棒性能。本文将围绕这一问题，研究一种新的鲁棒自适应控制方法，并将该方法用于NSV飞行控制系统设计。

3 单隐层神经网络干扰观测器设计

不确定系统控制问题研究中一种非常有效的处理系统不确定性的方式是通过对系统中不确定性进行估计，然后利用估计值设计补偿控制律以抵消不确定性的影响，达到提高原有控制器性能的目的，因而估计器对不确定的估计精度和估计速度将直接影响最终的控制效果。本节中将首先利用单隐层神经网络的逼近能力和被控对象分析模型的有用信息研究一种新的不确定性估计方式，其结果不仅能够替代已有的结果，还有可能表现出更加优异的估计性能。

本文采用的SHLNN输入输出映射矩阵以及可调参数矩阵分别为其中bv=l为偏项，x=

根据文献[8-l0]，可以做如下假设：

假设3对于给定任意逼近误差上界＞0，存在有限隐层神经元数和理想的权值矩阵（W*，V*），使得神经网络在紧集Dx上一致逼近系统（l）中连续光滑未知的d，即

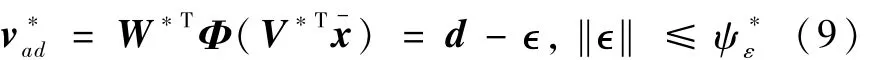
假设4若定义理想权值为

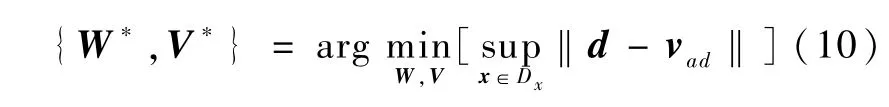
假设W*、V*有界，即则亦有界。

定义神经网络权值误差为则求得

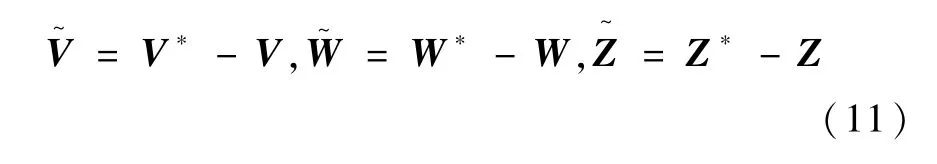
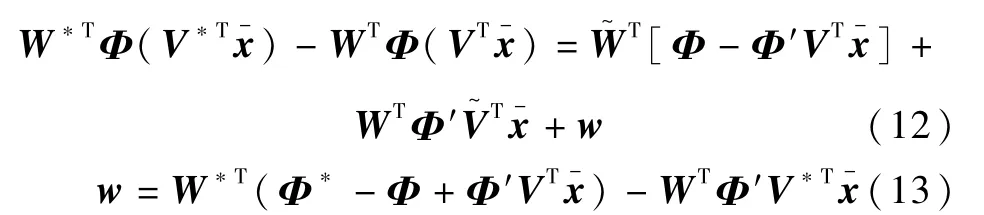
现考查

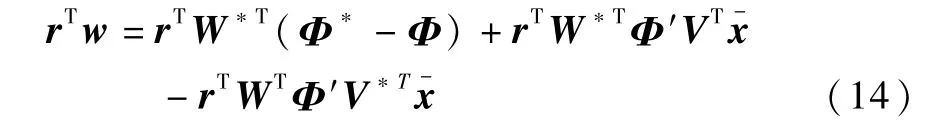
其中r∈Rn3×l。由于（Φ*-Φ）中每个元素上界都为l[l0]，所以有下列不等式成立

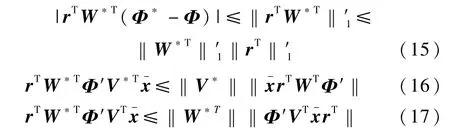
其中矩阵范数‖·‖′l定义为矩阵元素绝对值的和。所以

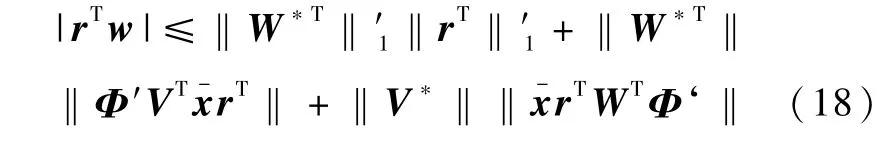
令

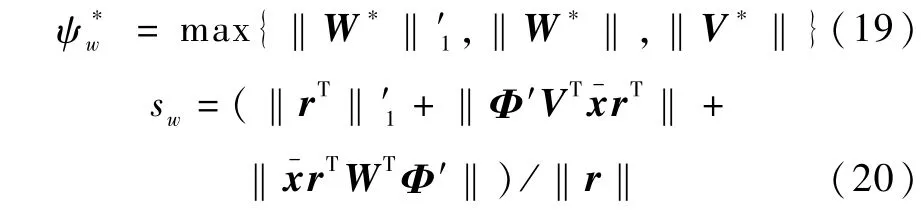
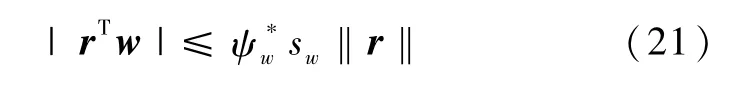
再令

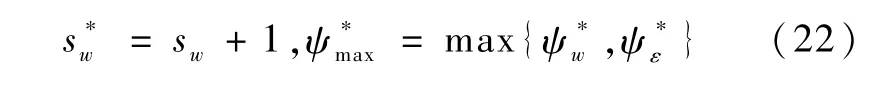
定理1.考虑如下动态系统

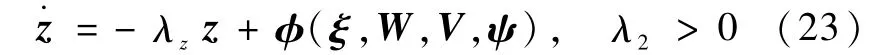
其中φ=λzξ+f（ξ）+gl（ξ）μ+g2（ξ）[vad+vr]。若定义干扰观测器名义误差为

同时定义自适应鲁棒控制输入如下

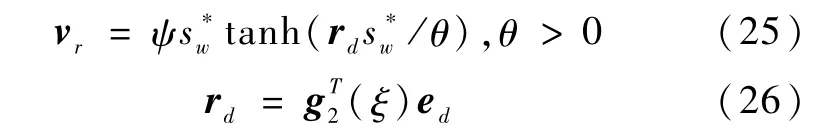
其中神经网络自适应律选为

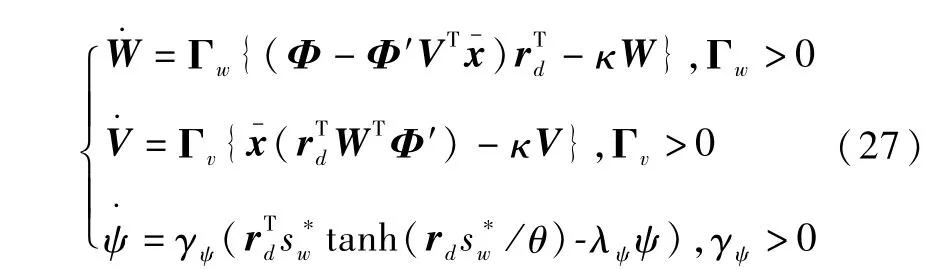
则观测误差ed及神经网络权值有界。

证明：由式（l）、（9）和（23）可知

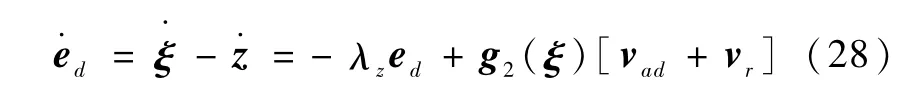
代入式（l2）可得

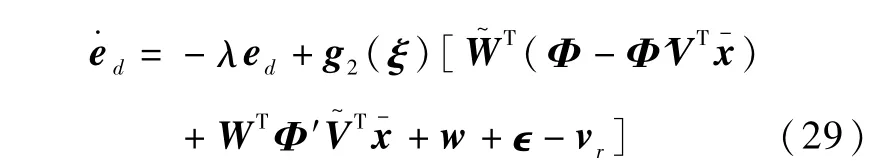
选择Lyapunov函数

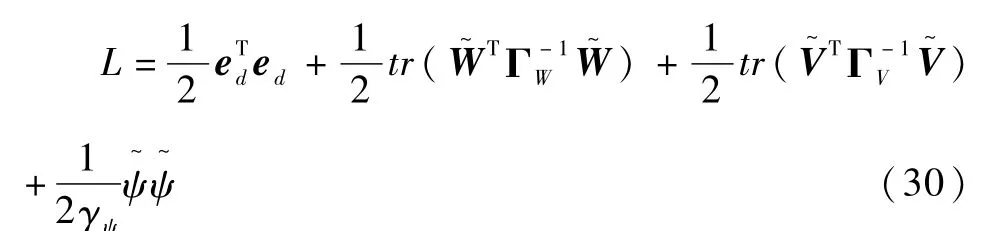
对时间t求导，并代入（25）-（29）可得

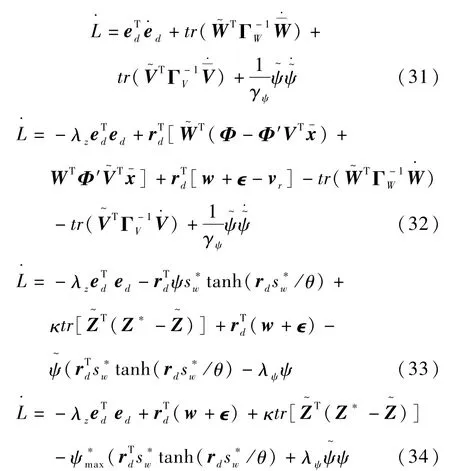
考虑式（l8）及下列不等式

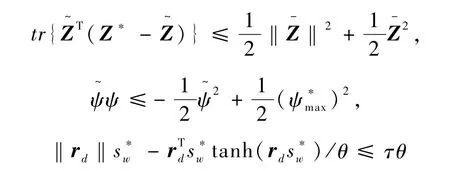
有

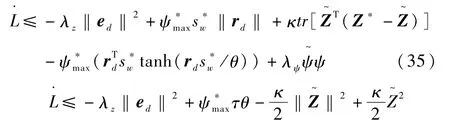
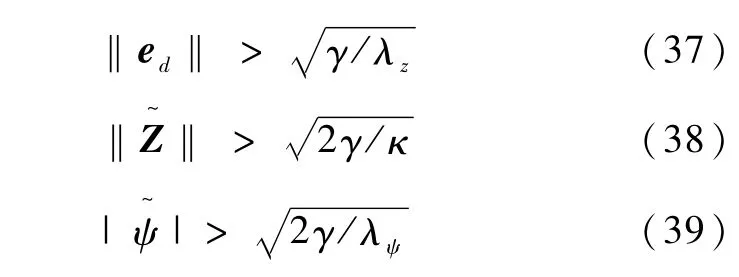
注1定理l以严格的形式证明出由式（23）给定的SDO对系统中未知不确定的逼近能力，且SDO对系统不确定的逼近和控制输入μ的形式无关，所以已有的很多线性和非线性控制方法都可以用它来改善不确定性存在条件下的控制性能。但同时需要注意的是，定理l的证明过程中没有考虑闭环系统e的有界性，因此在与具体方法结合时，有必要在自适应律式（25）-（27）的基础上稍加改动来保证闭环系统所有信号有界。

4 基于TLC方法的鲁棒自适应控制

本节将把SDO技术与TLC方法结合获得改进的鲁棒自适应控制方法。考虑式（2）成立，利用SDO输出构建两个新的控制输入分别为：

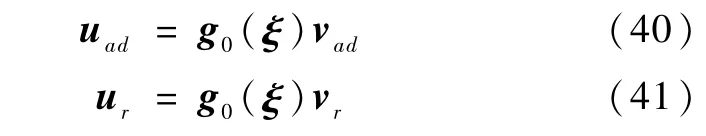
则总的控制输入改写成

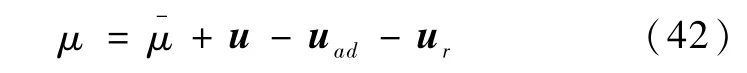
代入式（4）并整理可得

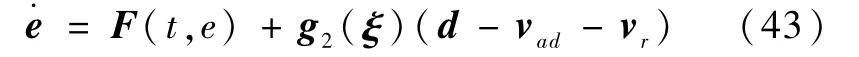
引理1对于n维连续时间线性时变系统=Ac（t）e，原点为唯一平衡状态，n×n矩阵Ac（t）的元均为分段连续的一致有界函数，则原点是一致渐近稳定平衡点的充要条件是：对任给的一个实对称、一致有界、一致正定的时变矩阵Q（t）∈Rn×n，即存在两个实数βl、β2＞0使有

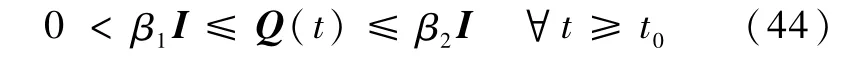
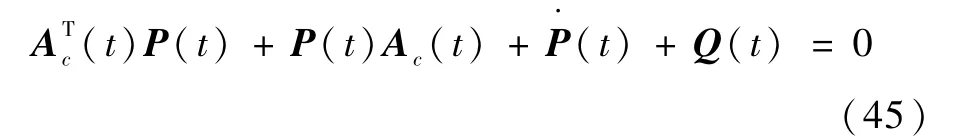
则Lyapunov方程的n×n的解阵P（t）为实对称、一致有界、一致正定，即存在两个实数αl、α2＞0使有

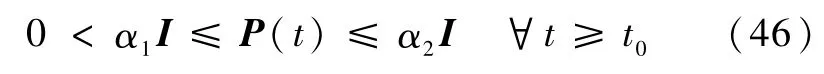
假设5存在正实数βl、α2满足：

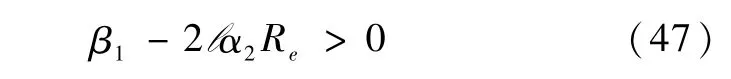
定理2对于由式（l）和式（23）组成的复合系统，在满足假设l-5的条件下设计鲁棒自适应控制律

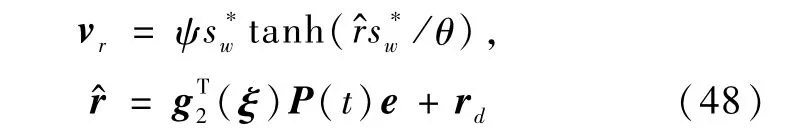
神经网络鲁棒自适应调节律选为：

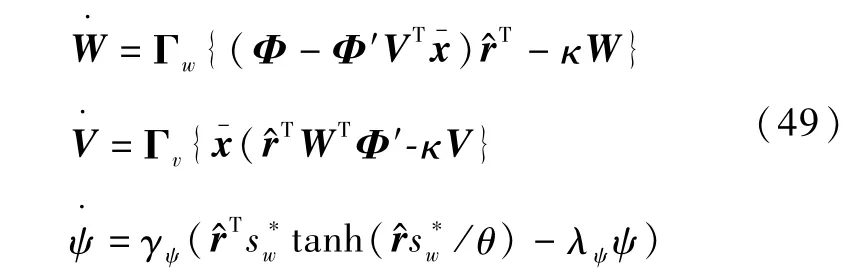
则闭环系统所有信号有界。

证明：将式（8）、（l2）代入式（43）可得

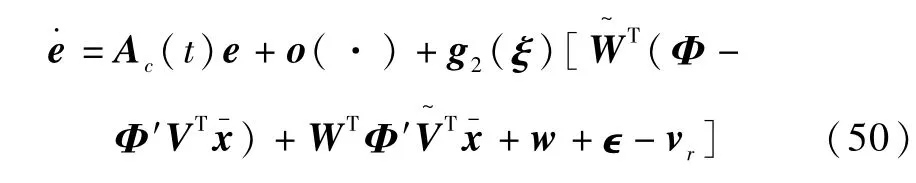
选择Lyapunov函数为

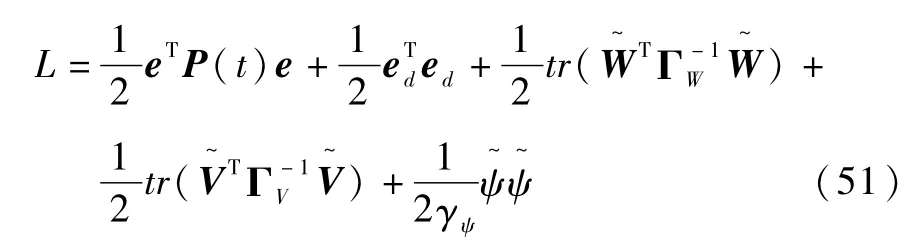
将L对时间t求导并代入式（50）可得

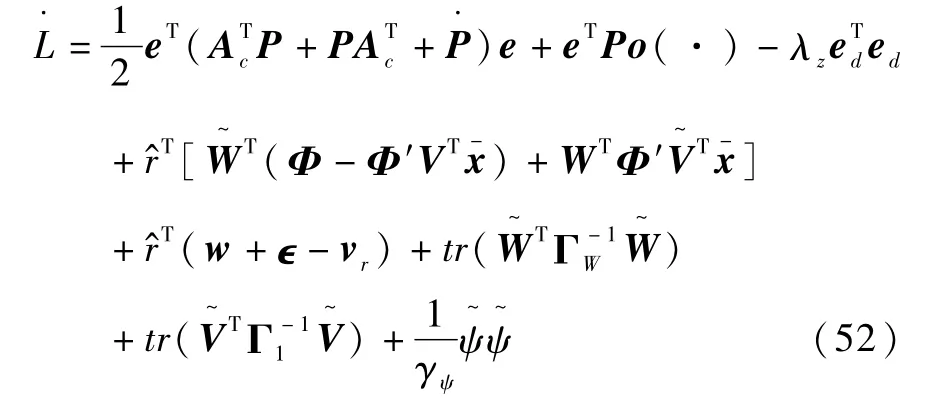
根据式（45）、（48）和（49）可得

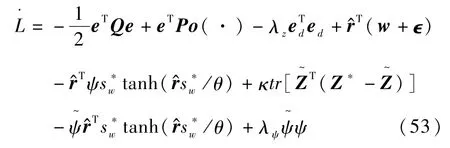
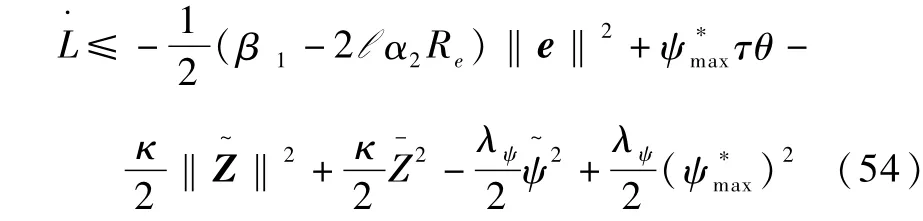
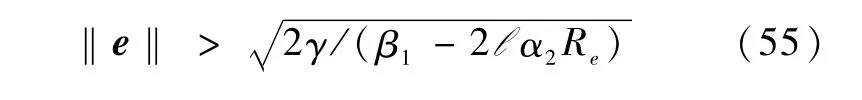
由假设5，则在不等式（37）、（38）、（39）及不等式任一成立的条件下有＜0成立。因此闭环系统所有信号保持有界，且可以通过选择合适的设计参数，使得系统误差收敛至任意小紧集。证毕。

5 近空间飞行器飞行控制系统仿真验证

5.1 数学描述和控制系统实现

NSV的飞行控制系统描述为[3]：

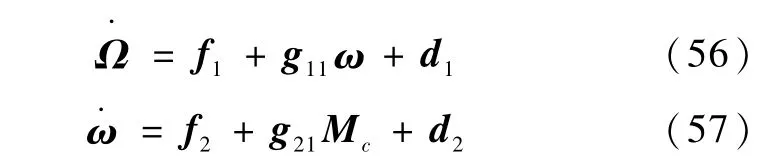
式中：Ω=[α，β，σ]T为姿态角向量，ω=[p，q，r]T为姿态角速度向量，MC为滚动、俯仰、偏航方向上的控制力矩。fl、gll、f2、g2l的详细表达式参考文献[3]。dl、d2∈R3表示内外回路中存在的不确定性。

本文的控制方法实现过程与参考文献[3]中的3.2-3.6小节所得结果的表达式完全相同，差别仅在于文献[3]中式（54）和（55）的和将由本文设计的鲁棒自适应控制器代替。因此，不妨记外内回路最终控制输入为：

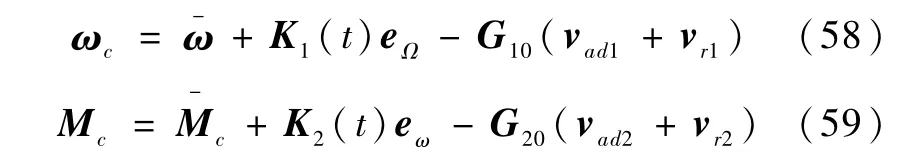
5.2 仿真验证

在与文献[3]相同的TLC设计参数和相同的飞行条件下，实现内、外回路鲁棒自适应控制律所需的参数均选为：Q（t）=0.5I6-6，nl=l2，n2=l0，n3=6，λz=20，κ=2，ΓW=5Ill×ll，ΓV=5Il3×l3，γψ=5，λψ=0.2，θ=0.l。

仿真过程以多种气动参数不确定条件对TLC方法和本文方法进行对比验证。当对象模型气动参数不确定性在0至-50%之间变动时，TLC方法响应性能差别不大，均可以提供较满意的跟踪性能，但是当气动参数不确定性超过-50%时，TLC控制明显下降。图l至图3中虚线分别表示气动参数存在-50%、-60%和-70%不确定条件下采用TLC控制方法时NSV姿态角响应曲线。图3中TLC方法已经完全失效。图l至图3中实线给出本文研究的鲁棒自适应控制方法的响应曲线，虽然在图3中仍然存在稍许波动，但仍能跟踪上期望的姿态角命令。考虑到气动参数-70%不确定已经是相当恶劣的条件，这些结果表明鲁棒自适应控制律的加入大大提高了TLC方法的干扰衰减特性和鲁棒特性。

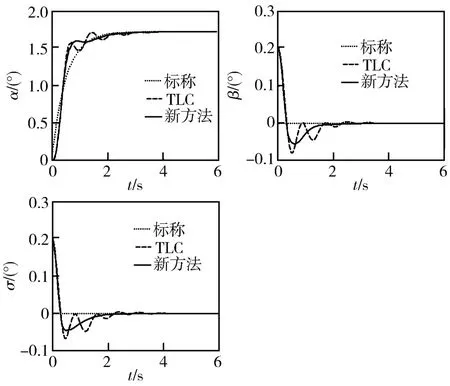
图l 姿态角响应曲线（-50%不确定性）

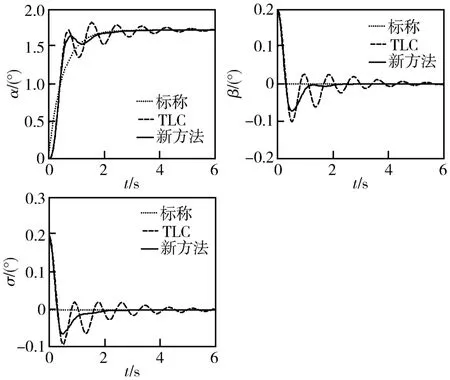
图2 姿态角响应曲线（-60%不确定性）

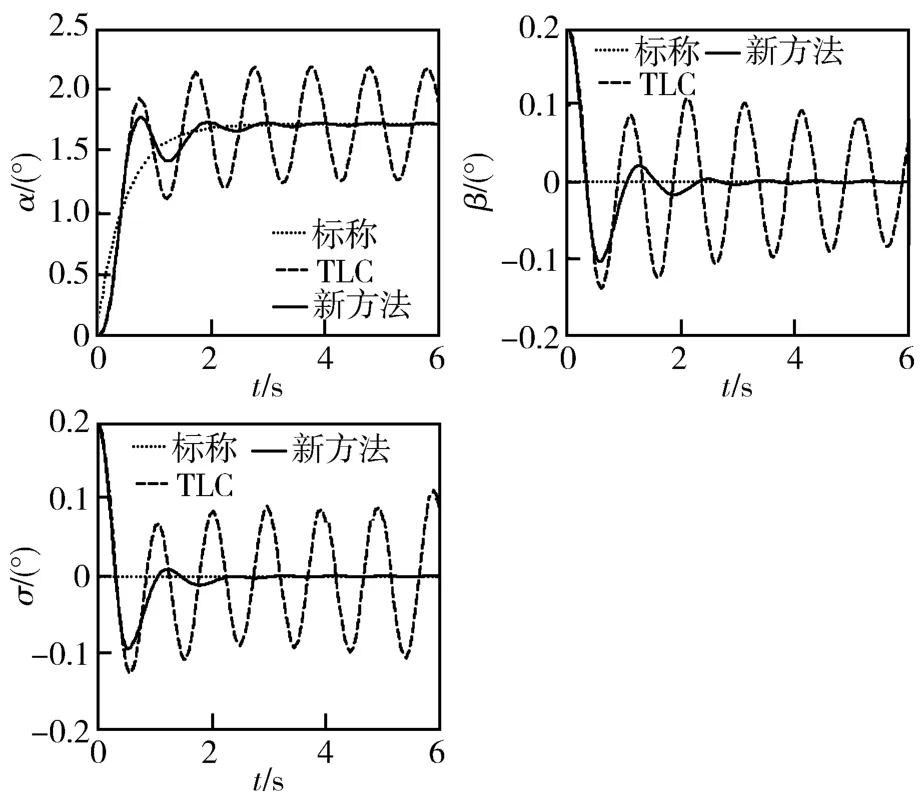
图3 姿态角响应曲线（-70%不确定性）

6 结论

近空间飞行器在高超声速飞行条件下的高精度、高稳定度控制问题给控制系统设计带来极大挑战。本文首先研究了一种通用的不确定性估计器设计方法，可以利用它的输出构建补偿控制律以抵消系统不确定性对很多线性/非线性控制方法性能的影响。将该方法与轨迹线性化方法结合得到新的鲁棒自适应控制策略。近空间飞行器高超声速飞行条件下的仿真验证表明，该方法具有更加稳定、可靠的控制性能和更加准确的控制精度。

[l]尹志忠，李强.近空间飞行器及其军事应用分析[J].装备指挥技术学院学报，2006，l7（5）：64～68

[2]Fidan B，Mirmirani M，Ioannou P A.Flight dynamics and control of air-breathing hypersonic vehicles：review and new directions[C].The l2 th AIAA International Space Planes and Hypersonic Systems and Technologies Conference and Exhibit，Dec.l5-l9，2003，Norfolk，USA

[3]朱亮，姜长生，陈海通等.基于单隐层神经网络的空天飞行器直接自适应轨迹线性化控制[J].宇航学报，2006，27（3）：338～344

[4]朱亮，姜长生，张春雨.基于径向基神经网络干扰观测器的空天飞行器自适应轨迹线性化控制[J].航空学报，2007，28（3）：673～677

[5]Bevacqua T，Best E，Huizenga A.Improved trajectory linearization flight controller for reusable launch vehicles[C].The 42nd AIAA Aerospace Sciences Meeting and Exhibit，Jan.5-8，2004，Nevada，USA

[6]Kahlil H K.Nonlinear systems[M].New Jersey：Prentice-Hall，2002，80～l20

[7]Zhu J J.PD-spectral theory for multivariable linear timevarying systems[C].The 36th Conf.on Decision&Control，Dec.l0-l3，l997，San Diego，USA

[8]Nardi F.Neural network based adaptive algorithms for nonlinear control[D].Georgia Institute of Technology，2000

[9]Polycarpou MM.Stable adaptive neural control scheme for nonlinear systems[J].IEEE Transactions on Automatic Control，l996，4l（3）：447～45l

[l0]Zhang T，Ge S S，Huang C C.Design and performance analysis of a direct adaptive controller for nonlinear systems[J].Automatica，l999，35（11）：l809～l8l7

Robust Adaptive Contro1 for Near Space Vehic1e Based on Trajectory Linearization Method

JING Zhongliang，ZHU Liang，LU Ping，HU Shiqiang
（Institute of Aerospace Science&Technology，Shanghai Jiao Tong University，Shanghai 200240，China）

A robust adaptive flight control scheme is presented for a near-space vehicle（NSV）.A novel estimator design technique called the single hidden layer neural network disturbance observer（SDO）is developed.The SDO utilizes both the universal approximation property of neural network，and more useful information on the controlled system.A new robust adaptive control algorithm is proposed by integrating the existing trajectory linearization control（TLC）method with the SDO technique.Conditions are derived which guarantee ultimate boundedness of all the errors in the closed-loop system.Finally，the flight control system of the NSV is imp lemented by using the proposed method.Excellent disturbance attenuation ability and strong robustness of the proposed method are demonstrated.

flight control，nonlinear system control，robust adaptive control，hypersonic vehicle