带干扰补偿的挠性航天器变结构输出反馈控制

郭廷荣

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

带干扰补偿的挠性航天器变结构输出反馈控制

郭廷荣1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

研究了在控制量受限的情况下，挠性航天器的变结构输出反馈和干扰补偿的控制方法。在控制律的设计中，用变结构输出反馈控制来抑制挠性附件的振动，用扩展状态观测器对系统的不确定性和干扰力矩进行估计并给予实时补偿。仿真结果验证了该方法的有效性。

挠性航天器；变结构控制；输出反馈；扩展状态观测器

1 引 言

随着航天技术的发展，航天器结构也变得越来越复杂，通常这些带有大型挠性太阳能帆板或其它轻型结构的挠性附件的航天器，随着燃料的消耗和附件的展开或收拢其转动惯量变化很大，这些因素造成了研究对象具有很大的不确定性，对姿态控制精度的影响越来越严重，因此需要其控制器具有较强的鲁棒性。

变结构控制是一种对不确定系统进行有效控制的方法，具有良好的鲁棒性，它的主要优点是系统在滑动平面上运动时，对内部参数变化和外部扰动具有不敏感的特性，在航天器的控制上得到了广泛的应用[1-3]。通常变结构控制使用全状态信息进行反馈控制，而挠性结构的各阶模态不可测，文献[2]提出了变结构输出反馈控制方法，不要求全状态可测，但其在控制器设计中，总是要求执行机构能够提供足够的控制力矩来克服系统的各种不确定性因素，而没有考虑在实际应用中执行机构的输出力矩总是有限的问题。

为获得高稳定度的姿态控制，可考虑引入各种补偿律，以补偿系统中的不确定扰动的影响。因为扩展状态观测器（ESO，extended state observer）对非线性不确定系统具有快速跟踪能力[4-5]，可采用其对不确定扰动进行估计并给予在线补偿，以减小控制器对模型的依赖。本文根据变结构和自抗扰干扰补偿控制的机理，针对一类挠性航天器的姿态稳定控制问题，设计了变结构输出反馈与干扰补偿相结合的控制方案，并进行了仿真研究，取得了良好的控制效果。

2 挠性航天器数学模型

考虑一类带有大挠性附件的航天器模型。将卫星中心体视为刚体，取姿态角和附件振动模态为广义坐标，建立挠性航天器的动力学方程为[6]

其中，J∈R3×3为航天器的转动惯量阵；ω∈R3×1为卫星角速度；Tc∈R3×1与Td∈R3×1分别为控制力矩和干扰力矩；f1，f2分别为高阶非线性项（仅考虑挠性模态的前N阶振动频率）；q、ζ和Λ分别为挠性附件的模态向量、阻尼矩阵和模态角频率阵，Br为挠性附件的转动耦合系数。

定义姿态角Φ=[φ θ ψ]T，φ、θ和ψ分别表示星体的滚动角、俯仰角和偏航角。因为在三轴稳定控制过程中，这些角度均为小量，所以姿态运动角速度可以表示为

其中，

f（t，x）代表系统的非线性部分和模型截断所引起的不确定性部分。，饱和函数sat（u（t））是考虑到由于执行机构的饱和特性而引起的非线性，其定义为：sat（u（t））=ε·u（t）。

式中0＜ε≤1，定义为

这里umax为执行机构的饱和值。

假设系统满足以下条件：系统矩阵（A，B，C）可控可观；f（t，x）=Bg（x，t），且‖g（x，t）‖≤κ，‖·‖表示欧氏范数。

3 控制器设计

在本文研究中，航天器姿态控制系统的敏感器为陀螺和星敏感器，分别测量星体的角速度和姿态角。由于挠性各阶模态不可测，本文利用输出信息设计输出反馈变结构控制器，同时利用扩展状态观测器对系统的不确定性扰动进行实时观测并给予动态补偿，从而降低不确定性扰动对系统的影响，减小系统的稳态误差。控制系统原理框图如图1所示。

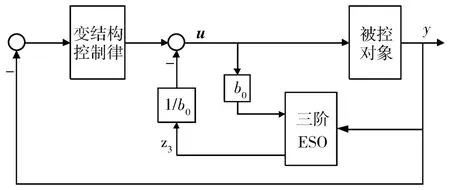
图1 控制系统原理图

控制器由两部分组成：u=uvs+uc

其中，uvs为变结构输出反馈控制器，uc为ESO补偿控制器。

3.1 变结构输出反馈控制器设计

本文在文献[2]的基础上加以改进，考虑了输入控制受限的姿态变结构控制问题。选择滑模面

式中G∈R3×6为滑面选择矩阵。选取如下形式的线性控制与非线性控制相结合的控制律

其中，N∈R3×6是常值增益矩阵，α是标量，ud是非线性控制器，选为ud=s/‖s‖，为了避免变结构控制中的颤振问题，可修改控制量为ud=s/（‖s‖+δ0）或ud=s/（‖s‖2+δ0），δ0＞0。滑动平面的非奇异变换并不改变滑动模态的动态特性，如选择一个滑动平面sI=GIy，那么可利用G=，把滑动平面转换成s=Gy。不失一般性，假设GCB=I。定义GC的奇异值分解为GC=UΣVT，其中，

定理1.对于式（6）给出的控制律，选择N=-（r I+GCAVΣ-1UT）G，其中r＞0是标量，如果选择α＞（‖GCA‖Ω+κ）/ε，Ω＞0，则到达条件对于｛x∶‖xk‖+‖xp‖＜Ω｝成立，其中，x分解为x=xk+xp，xk是GC的零空间x的一部分，即xk∈

证明.

因为x分解为x=xk+xp，xk是GC的零空间x的一部分，即，所以GCx=GCxp，简化右端第一项

如果GC=UΣVT，那么存在某个向量β，使得xp=Vβ，又因为VTV=I，UTU=I，则

对于欧几里得空间的同类矩阵范数，由矩阵相容性，得

3.2 干扰补偿控制器的设计

变结构控制中参数的选取是根据系统中最大可能范围来确定的，可能给出过大的控制量，且系统中的不确定性因素很难精确地描述，因此很难获得控制器中的参数范围，将导致α，r值的选取过大，影响控制系统的性能。扩展状态观测器对非线性不确定系统具有良好的快速跟踪能力，能对不确定性因素进行估计，减小控制器对模型的依赖。

ESO给出系统总扰动量的估计z3（t），用扰动估计量补偿器生成控制信号。

扩展状态观测器的基本思想是：通过构造特定的非线性函数实现对系统扩展状态变量的在线估计。

三阶扩展状态观测器算法如下[4]：

式中，yI=Φ，fal（e，α，δ）为非线性函数：

通过ESO中β1、β2和β3参数的合理选择，使ESO稳定，且以一定的速度跟踪系统的各状态，即

4 数学仿真

取挠性航天器的惯量及帆板转动耦合系数如下

耦合系数矩阵：

模态频率矩阵=diag｛0.107，0.258，0.667｝Hz

模态阻尼矩阵：ζ=diag｛0.005，0.005，0.005｝

三轴姿态角初始值分别为φ0=0.04°，θ0=0.04°，ψ0=0.04°，三轴姿态角速度初始值分别为ωx0=0.000 2（°）/s，ωy0=0.002（°）/s，ωz0=0.000 2（°）/s。

三阶扩展状态观测器（ESO）参数分别为：

变结构控制器参数选取γ=1.5，α=0.5，消颤因子选取0.005，最大控制力矩为0.2 N·m。

在200 s时，对卫星作用幅值为0.2 N·m、脉宽20 s的外干扰。图2和图3给出了偏航通道的ESO对姿态角和总扰动的估计值与实际值比较的仿真曲线，图4给出了控制力矩。

图2 姿态角ψ的实际值与估计值的比较

图3 总扰动的实际值与估计值的比较

图5为补偿前后姿态角的响应对比，图6为补偿后挠性结构的一阶、二阶、三阶模态响应。

图4 偏航通道的控制力矩

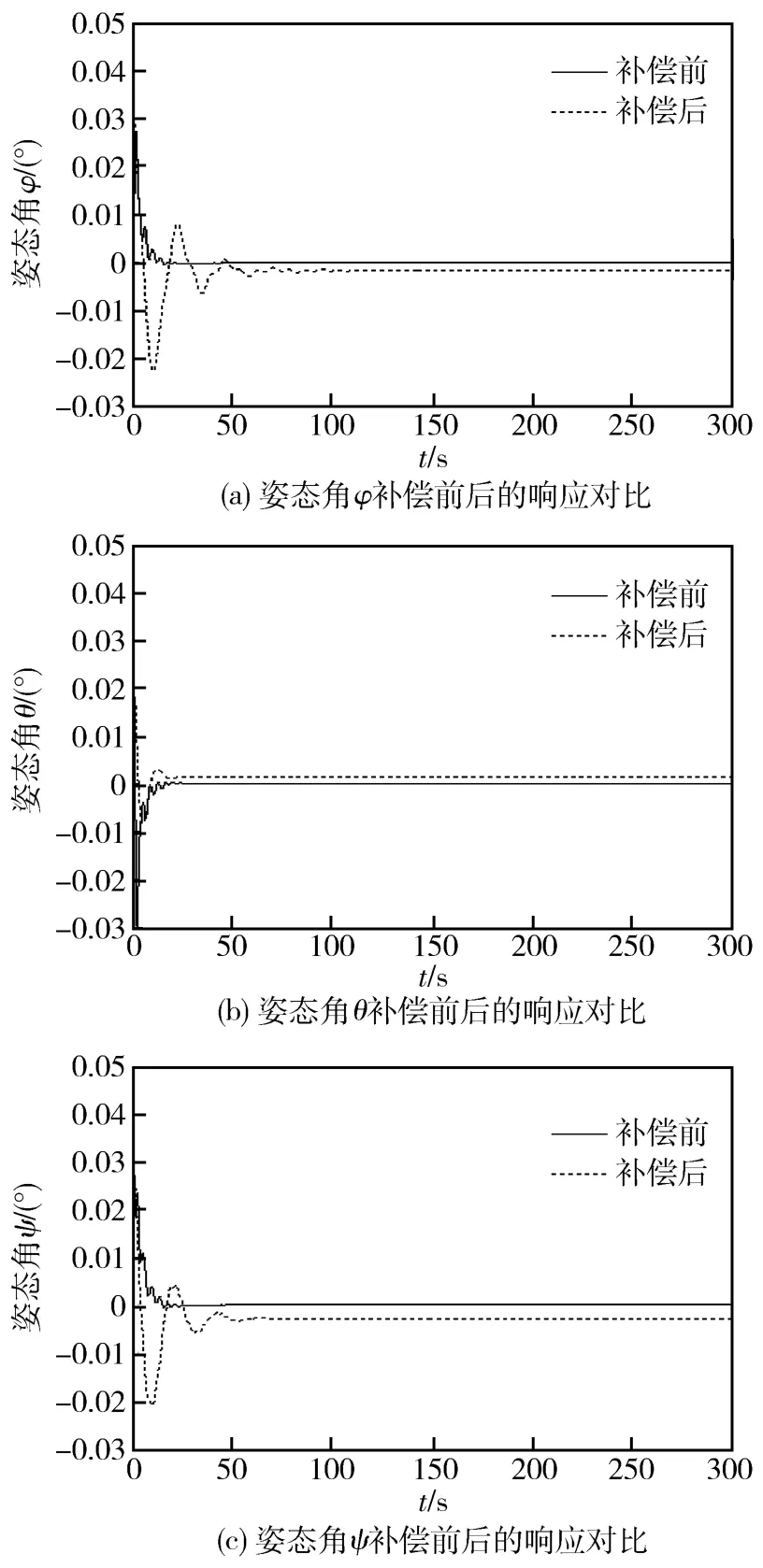
图5 补偿前后姿态角的响应对比

仿真结果表明，输出反馈变结构能很好地抑制挠性体振动，加入基于ESO的干扰补偿控制器后，改善了系统的稳定性能，加强了滑动过程中的抗干扰能力，姿态指向精度较补偿前有提高，补偿后在一定程度上克服了不确定因素对系统的影响。

图6 补偿后挠性结构的一、二、三阶模态响应

5 结 论

本文针对挠性航天器本身所存在的模型不确定性因素、外部扰动的作用以及控制受限的问题，研究了一种利用输出信息的变结构输出反馈和干扰补偿的控制方法。仿真结果表明，本文提出的控制方法效果良好，具有一定的应用价值。

[1] Lo C，Chen Y P.Smooth sliding mode control for spacecraft attitude tracking maneuvers[J].Journal of Guidance，Control and Dynamics，1995，18（6）：1345-1349

[2] Yallapragada S V，Heck B S，Finney J D.Reaching conditions for variable structure control with output feedback[J].Journal of Guidance，Control and Dynamics，1996，19（4）：848-853

[3] Boskovi J D，Li S M，Mehra R K.Robust adaptive variable structure adaptive control of spacecraft under control input saturation[J].Journal of Guidance，Control and Dynam ics，2001，24（1）：14-22

[4] 韩京清.自抗扰控制器及其应用[J].控制与决策，1998，13（1）：19-23

[5] 黄一，韩京清.非线性连续二阶扩展状态观测器的分析与设计[J].科学通报，2000，45（13）：1373-1379

[6] 屠善澄.卫星姿态动力学与控制[M].北京：宇航出版社，2001

Variab le Structure Output Feedback Control with Disturbance Compensation for Flexible Spacecraft

GUO Tingrong1，2
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

A variable structure output feedback control method with disturbance compensation is presented under control torque saturation for the flexible spacecraft.In this method，the variable structure output feedback control suppresses the vibration of flexible appendages，the unknown dynamics and disturbing torques are estimated by an extended state observer and are compensated on line.The simulation results show the method is effective.

flexible spacecraft；variable structure control；output feedback；extended state observer

V448.22

A

1674-1579（2008）05-0041-04

2008-01-15

郭廷荣（1976-），女，黑龙江人，博士研究生，研究方向为航天器控制（e-mail：trguo@163.com）。