基于线性二次型的飞控参数故障渐近调节*

2008-12-12尹晓睿

空间控制技术与应用 2008年5期

关键词：最优控制控制率延时

尹晓睿，杨浩，2，姜斌

（1.南京航空航天大学自动化学院，南京210016；2.里尔科技大学LAGIS实验室，法国59655）

基于线性二次型的飞控参数故障渐近调节*

尹晓睿1，杨浩1，2，姜斌1

（1.南京航空航天大学自动化学院，南京210016；2.里尔科技大学LAGIS实验室，法国59655）

研究了含有参数故障的线性系统，提出了一种基于线性二次型的控制策略。采用该渐近调节反馈控制律，可以减小系统由于容错控制算法时延所致的性能下降。针对某飞机模型进行了仿真，结果验证了所提出策略的有效性。

渐近调节；线性二次型；反馈控制；容错控制

1 引言

容错飞控系统可显著提高飞机的可靠性和生存能力，并能使飞机在危急或者损伤的情况下仍保持良好的性能[1]。在故障诊断和容错控制中，由实际物理系统所造成的延时往往容易被忽略[2]，当发生故障后，通过计算所得到新的控制律只有在一定延时后才能作用于故障系统[3]，而在这段时间，故障系统仍旧运行在原有的控制律下，可能会导致系统性能大幅下降。

本文将文献[4]中的基于渐近调节的容错控制方法进行扩展，给出适用该方法的充分条件，并将其运用到带有执行器故障的Boeing 747-100/200航空系统，还对系统在渐近调节控制下和经典控制下的能耗做了对比并展开相应的讨论。接着描述了基于二次型的容错控制问题，给出了经典的故障调节法的限制，然后介绍并分析了渐近调节方法，最后对实际飞机模型进行仿真。

2 基于线性二次型的最优控制

2.1 一个最优控制问题的提出

正常线性系统如下

故障发生后系统变为

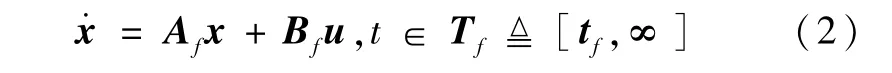
其中，状态向量x∈Rn，输入向量u∈Rm，tf＞0是系统从正常状态转换到故障状态的时刻，An，Bn和Af，Bf分别是相应维数的实矩阵，并且（An，Bn）及（Af，Bf）都是可控对。tf，Af，Bf由诊断算法给出，无时延、无误差。

控制目标是在将系统状态从初始值x（0）=x0转移到终值x（∞）且二次型能量函数

取最小值。其中，uT为矩阵u的转置，Q和R为对称矩阵且Q=DTD，R＞0且（D，An）和（D，Af）可检测。

根据最优控制理论，在每一个时间间隔Ta内，使式（3）达到最小最优解=n，f），Pα是下面代数Riccati方程的唯一正定解

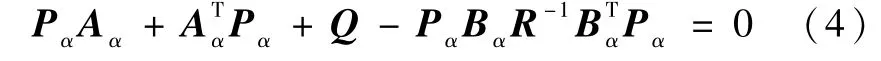
2.2 讨论

（1）参数故障不会改变平衡点，当故障发生后跟踪曲线x=0保持不变。

（2）（Af，Bf）正定且（D，Af）可检测，假定故障调节问题有唯一最优解。式（5）的下限值决定了可容许系统性能指标的下降。

（3）为了使其在尽可能短的时间内进行收敛，假定状态总有效。令y=Cnx，y=Cfx分别描述正常状态和故障状态下可用的传感器。在故障状态下，可以得出结论：只要（Cn，An）及（Cf，Af）可观测，可以建立状态观测器。

（4）如故障不可恢复（无解或解无意义），则需要进行重构。还有一个特殊情况就是故障使假定2和3都不成立。但本文中没有考虑状态重构情况。

（5）显然，理想的容错控制的假定是很难实现的，因为系统需要一定的时间进行故障诊断[5]。假设在时刻tf、tfdi和tftc均无诊断误差，系统运行过程可以分为以下4个时间段来进行分析：

1）[0，tf]，un控制系统[An，Bn]；

2）[tf，tfdi]为诊断时延，此时[Af，Bf]由un控制；

3）[tfdi，tftc]为故障调节时延，[Af，Bf]仍然由un控制；

4）故障调节完毕后，在[tftc，∞]时间段内，[Af，Bf]由新的控制率uf控制。

在实际控制过程中，tftc-tf的延时会使系统的性能大幅下降，无法令人满意。

渐近调节问题就是要尽量减小延时tftc-tfdi对系统性能造成的影响，并反复改进控制结果。

3 渐近调节

3.1 NR算法

NR算法：

Pi是以下Lyapunov方程（6）的唯一正定解。

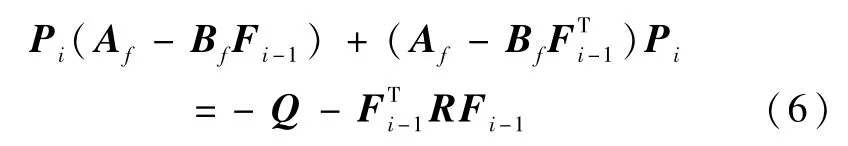
对于所有的i（i=1，2，…，n），Fi=R-1BTfPi，初始值F0已给出，F0为系统正常运行时的反馈矩阵。

文献[7]已经证明，如果Af-BfF0Hurwitz稳定，则这个算法可以得到以下结果：

1）对于所有i（i=1，2，…，n），Af-BfFi均Hurwitz稳定。

式7（b）中当等式成立时停止迭代。式7（c）中Pf是式（4）当α=f时的解。

“实时”特性：当决策时间不够长而导致结果不收敛时，可利用‘实时'特性。例如，某个算法，其特点是计算结果越精确，计算时间越长。那么解决这个决策问题的基本原理是：现在的解是最佳解其中的一个。

NR方案具有“实时”特性。渐近调节的理想情况是在[ti，ti+1]时段应用反馈控制率ui=-Fix，假设在系统延时阶段进行N次迭代，令ui=-Fix为系统在第i个时间段内的反馈控制律，则经过N次迭代后Fi将收敛于Ff。

当故障发生后，系统运行情况可以表示为

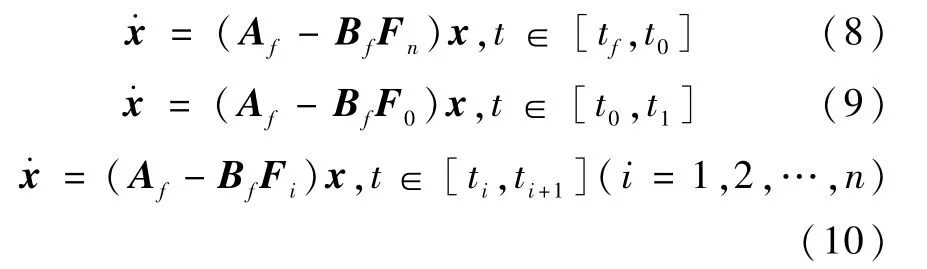
其中，t0、F0为运算的初始值（通常t0＞tfdi）。当故障被检测、隔离，或估计故障的幅值后，还需要一定的时间进行算法的初始化，最后证明了渐近调节算法的一些性质。

3.2 稳定性

定理1[4].如果Af-BfF0Hurwitz稳定，那么PA方案能使故障系统稳定。

如果故障系统在经典控制下没有出现失稳情况，初始化F0=Fn。如果Af-BfF0不稳定，则必须先找到稳定的反馈F0（（Af，Bf）稳定，F0一定存在），t0-tfdi这段时间用来搜索合适的F0。

3.3 最优性

本节讨论PA算法的最优性，当迭代次数N＞1时，初始值为F0的算法（5）能得到F1，F2，…FN。

CA算法先计算反馈FN再将其运用到故障系统，得到故障后的两种控制状态分别为

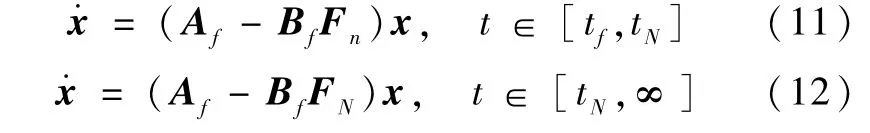
而PA算法逐渐改变控制率Fi，例如，系统的闭环矩阵Af-BfF0作用在[t0，t1]时间段，而Af-BfFi作用在[ti，ti+1]（i=1，2，…，n）。其实，经典控制算法CA和渐近调节算法PA仅在时间段[t0，tN]采用不同的控制率，如果N足够大，收敛必定存在。

定理2.如果闭环矩阵Af-BfFnHurwitz稳定，初始值F0=Fn，那么JPA≤JCA成立。

证明.分为三部分：

1）设比较对：

经典控制算法的控制序列如下（初始化F0=Fn）

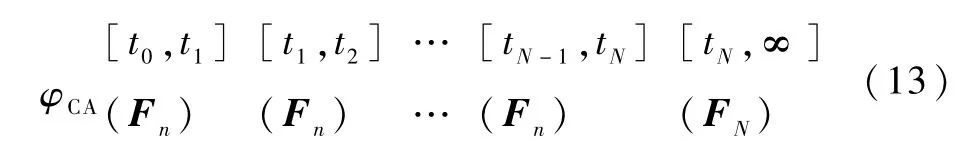
渐近调节控制序列

k=1，2，…，N-1时，定义控制序列族为

令φ0=SCA，显然，SN-1=SPA。

在k=1，2，…，N-1时，只需比较Sk和Sk-1的值就可以证明J（φk）≤J（φk-1）成立。

状态Sk和Sk-1的轨迹在[t0，tk]相同，所以时间段[tk，tN]有相同初始状态x（tk）。在[tk，tN]由于控制器不同，Sk和Sk-1的值不同，得到两种不同状态且Δk=tN-tk。

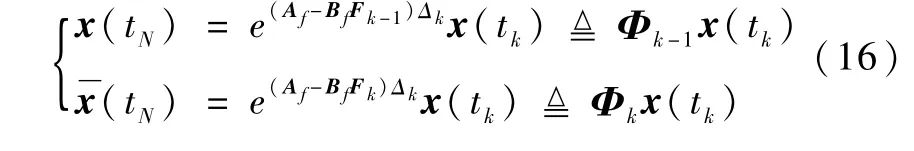
Sk和Sk-1的值在[tN，∞）也不一样，这是由不同的初始条件（14）造成的。而且，只要反馈Fn稳定，那么所有的反馈矩阵Fk都稳定，且Fk与方程（4）的解Pk有关，

2）计算：

与Sk-1相关的J（φk-1）的表达式如下

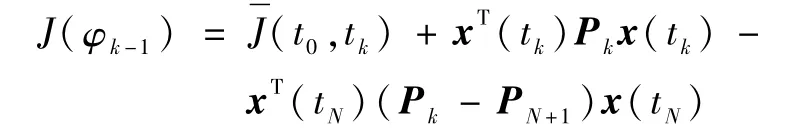
再利用等式（16），得

同理，可得与Sk相关的值

3）比较两个值：

为简化起见，用x来代替x（tk）。从式（17）和式（18）可以推导出

为了证明J（Sk-1）-J（Sk）＞0，先要证明

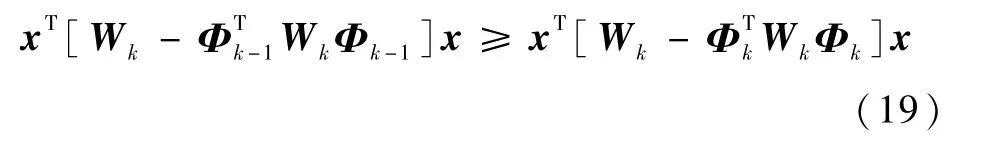
首先，因为对于所有的k，Wk-Wk+1≥0成立，且λmax（Φk）＜1，及Af-BfFk稳定。所以Wk-，能推出下式成立

为了证明式（17）成立，且从Φk-1和Φk定义中可以推出所以只需证明成立，或其等价式成立。

构造离散系统·z=-Bf（Fk-1-Fk）z及函数L=zT（Pk-1-Pk）z，对L求导

从Fk-1和Fk定义中可以推出

所以

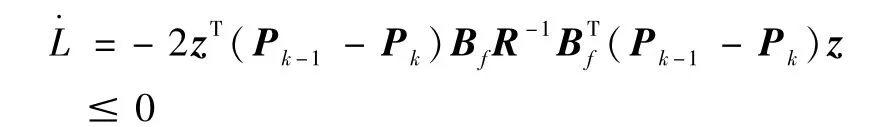
函数L正半定，其导数负半定，且当状态不为0时L的导数不恒为0，由文献[6]可知系统稳定，所以Wk≥0成立。

4 实例仿真

用于仿真的模型是线性化的Boeing747-100/200飞控系统[8]。含有12个状态变量，分别代表滚转速率、俯仰角速率、偏航角速率、空速、迎角、侧滑角、滚转角、俯仰角、偏航角、高度、X坐标和Y坐标。8个控制输入分别代表稳定偏转、副翼偏转、舵偏转、升降舵偏角和4个扰动。发生故障前，正常模型参数矩阵An见附录。

用于等式（3）中的加权矩阵

假定飞机升降舵偏角通道发生故障，其故障模型为

假定故障在tf=0.2 s时发生，在原来的控制率u0=-F0x的控制下，故障系统的性能显著下降。

根据渐近调节方法，经过7步迭代（初始值F0=Fn）得到新的控制率。假设故障诊断需要1 s，还需0.2 s检查Af-BfFn是否稳定，再加上一次迭代耗时0.5 s，所以直到故障发生后的t=4.9 s，经典控制中的反馈增益为Fn不变。当t=1.4 s时渐近调节算法的反馈增益为Fn，以后每间隔0.5 s依次转换为F1，F2，F3，F4，F5，F6，F7。应用NR算法计算得到F1～F7的参数矩阵见附录。图1给出了三种控制方法下的二次型能量函数J（u，x0，tf）=d t的比较（实线为渐近调节控制，虚线为经典反馈控制，点线为未加控制算法），根据最优控制理论的有限时间内最优控制定律可知，当控制率为u=-R-1BTPx、系统的二次型性能指标取极小时，即为最优控制[6]。

图1 三种控制方法下二次型能量函数的比较

从仿真结果来看，渐近调节控制的最优控制中的能量函数要小于经典控制，说明渐近调节优于经典反馈控制，这与图2状态变量的仿真结果相一致（实线为渐近调节控制，虚线为经典反馈控制，点线为未加控制算法）。

图2给出了12个状态变量在3种不同控制方法下的轨迹，仿真结果表明，运用渐近调节算法使俯仰角速率和空速等变量的阶跃响应的性能指标都优于传统控制，验证了算法的有效性。

渐近调节算法较好地解决了飞机发生故障所产生的延时后导致系统性能下降问题。渐近调节下的状态性能优于经典容错控制下的状态性能，并且在控制过程中能使能量函数取得较小的值。

5 结束语

本文采用渐近调节方法旨在解决普通容错控制延时过程中所出现的系统性能下降的问题，取得较好的结果。该方法基于线性二次型，并扩展得到‘实时性'法则，提高了系统的稳定性，改善了系统性能。将其应用于一个执行器故障的高阶飞机线性模型，取得了较好的效果。未来的研究方向包括提出更好的算法来解Riccati方程，分析实时性，以及改善普通模型和故障模型的不确定性的鲁棒问题。

[1] 李卫琪，陈宗基.非线性飞机对象操纵面故障的控制律重构[J].北京航空航天大学学报，2003，29（5）：428-433

[2] 胡昌华，许化龙.控制系统故障诊断与容错控制的分析和设计[M].北京：国防工业出版社，2000，166-169

[3] Jiang B，Marcel S，Vincent C.Fault accommodation for a class of nonlinear systems[J].IEEE Trans.Automatic Control，2006，51（9）：1578-1583

[4] Marcel S，Yang H，Jiang B，Progressive accommodation of parametric faults in linear quadratic control[J].Automatica，2007，43（12）：2070-2076

[5] 王仲生.智能容错技术及应用[M].北京：国防工业出版社，2000，56-60

[6] 姜长生，孙隆和.系统理论与鲁棒控制[M].北京：航空工业出版社，1998，283-285

[7] Kleinman D L.On an iterative technique for Riccatiequation computation[J].IEEE Trans.Automatic Control，1968，Vol.AC-13：114-115

[8] Marcos A，Balas G J.Linear parameter varying modeling of the Boeing 747-100/200[C].AIAA Guidance，Navigation and Control Conference，August，2001，Montreal，Canada

The Linear Quadratic Form Based Progressive Accomm odation of Param etric Faults in Aircrafts

YIN Xiaorui1，YANG Hao1，2，JIANG Bin1，
（1.College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.LAGIS Lab，Lille University of Science and Technology，59655，France）

This paper deals with the linear systems with parametric faults.A control strategy based on the linear quadratic form is proposed.It significantly reduces the degradation of performance that results from the time delay needed for the fault tolerant control algorithm.Simulations on an aircraft model show the efficiency of the proposed method.

progressive accommodation；linear quadratic form；feedback control；fault tolerant control