列方程解应用题的几个技巧

刘秀霞

列方程解应用题在初中数学中既是重点，又是难点，有些学生对于方程中数量之间的相依关系及其变换往往识别不清，遇到一些特殊的应用题，更是无从下手，找不到相等关系．如何寻找相等关系，把问题从杂乱的条件中理出头绪，使问题得以解决，我认为应注意以下几个方面的问题．

一、注意弄清和掌握基本数量关系

寻找相等关系，首先要弄清并掌握各类应用题中的基本数量关系，如在行程问题中，基本关系有：距离=速度×时间；在劳力调配问题中，基本数量关系有：原有劳力+调配劳力=现在劳力；在利润率问题中，基本数量关系有：商品利润=商品售价-商品进价，商品利润率=商品利润÷商品进价，然后依着这些数量之间的相等关系，列出有关的代数式并列出方程．

【例1】 商品对某种商品作调价，按原价的8折出售，此时商品的利润率是10，此商品的进价为1600元，商品的原价是多少?

分析：本题中依着的数量关系是，商品的利润率=商品利润÷商品进价．

解：设商品原价为x元，根据题意可列出的方程为：80x-1600/1600=10％.

二、注意理解关键性词语

有些应用题的数量关系，是通过题目中的一些关键性词语明显地表示出来，这些关键性词语常见的有：和、差、倍、分、大、小、多、少、相向、相遇、增加、减少、超过、提前等等．它们与列方程有着直接关系，解题时必须理解其确切的含义，然后就可以通过这些词语寻找相等关系，从而列出方程．

【例2】 某市居民2001年末的储蓄存款达到7079万元，比2000年末的储蓄存款的15倍还多了4万元，求2000年末的储蓄存款.

分析：本题中的关键性词语是“……15倍还多……”.

解：设2000年末的储蓄存款为x元，根据题意可列出的方程为：15x+4=7079

三、注意题目中的不变量

寻找相等关系，也可以从不变量入手，所谓不变量，就是一定的数量关系，在行程问题中，同向追及，则从出发到追及地或距离不变，或时间不变；相向相遇所走的距离和不变；在工程问题中总工作量不变；在劳力调配问题中，总人数不变；在等积变形中，体积不变等等．抓住了这些不变量，也就是找到了相等关系．

【例3】 将内径为200毫米的圆柱形水桶中的满桶水倒入一个内部长、宽、高分别为300毫米、300毫末、80毫米的长方形铁盒，正好倒满，求圆柱形水桶的高．

分析：本题中的不变量是圆柱体体积=长方体体积.

解：设圆柱形水桶的高为x毫米，列出的方程为：300×300×80=π(200／2)²x.

四、列表思维法

在分析应用题时，列表思维法能清晰地显现题意，通过列表、填空，由空与空之间的关系去寻找方程，从而为正确地解方程应用题奠定了基础，这类问题的特点是，设出两个或三个未知数，根据题意建立起两个或三个相等关系，从而列出方程组解答实际问题．

【例4】 小华买了10分与20分的邮票共16枚，花了2元5角，问：10分与20分的邮票各买了多少枚?

分析：将题意中的两个条件句抽成关键词语或公共词而列成行、列，制成表格，然后将题中的已知量和未知量填入表格中，从中找到他们之间的相等关系而列出方程组．

五、注意利用图示辅助分析

利用图示辅助分析就是在为解一些条件比较复杂的应用题寻找相等关系时，把题目中的数量及它们之间的关系，画成示意图，然后通过观察分析图中的数量，找出各种量之间的内在联系，从而找出相等关系，借助图形这些辅助工具，往往使问题更加直观，容易思考，使问题迎刃而解．

【例5】 有甲、乙、丙三筐苹果，先从甲筐取出苹果给乙、丙两篮，所给的个数等于原来各有的数，然后再由乙给甲、丙两筐现有个数，最后从丙给甲、乙两筐现有个数，互给后每个筐里有50个苹果，求甲、乙、丙三个筐内原有的苹果数.

分析：设甲筐有苹果x个，乙筐有苹果y个，丙筐有苹果z个，互给后的量变关系用图示表示如下：

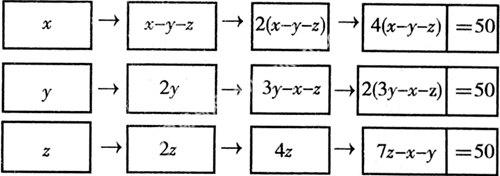
原有苹果数→从甲取出后→从乙取出后→从丙取出后

这样按照题设条件的先后顺序，步步由图展示，层次分明，使甲、乙、丙三筐互给后所有苹果的代数式自然地呈现出来，从而得出方程组．

还有行程问题，工程问题等用直线型示意图来一分析，比例问题，圆周运动问题等用圆形示意图来分析．

总之，寻找相等关系的方法要因题而异，但有一点，就是在变化的各未知数中，找不变量，从运动变化的关系中找相等稳定的相等关系，这样才能使复杂的数学问题简单化，达到事半功倍的效果．