简易导管的数值计算及分析

2008-04-24范露,罗薇,刘祖源等

中国舰船研究 2008年2期

1 引言

导管螺旋桨是特种推进器的一种，早在30年代就已经出现了,主要是为了提高功率系数Bp较高的高负荷螺旋桨的效率。它是在普通螺旋桨的外围装上一个套筒,套筒的纵剖面为机翼型或折角线型。这个套筒就称为导管,套筒可以是固定的,称为固定导管;也可以是转动的,称为转动导管。转动导管除了起导流作用外,还起着舵的作用。它有许多种形式,从导管中流场分有2种,包括加速型导管和减速型导管。导管中的螺旋桨工作时,与导管形成了—个整体,这时的流场与没有导管时的不同。对于加速型导管,首先,可以使螺旋桨盘面处的水流加速,使螺旋桨工作在较大的速度场,从而可以提高螺旋桨的效率。其次,由于导管出口处的面积逐渐扩大,尾流的收缩极小,使轴向诱导速度减小,也有助于提高螺旋桨的效率。最后,由于叶梢和导管的间隙很小,由叶面和叶背的压力差引起的绕流大大减小,其能量损失也就减小。正是由于这些原因，加速导管螺旋桨具有效率高,推力大,在风浪中的性能较好等特点。对于功率系数Bp较高的高负荷螺旋桨,采用它所能达到的效率,将远远超过常规螺旋桨,特别是在系泊情况下,可将系泊推力提高30%以上。

国外发表的导管螺旋桨系列试验资料中，以荷兰船模试验池的No.19A+Ka螺旋桨系列最为著名。随后，为改善后退性能又提供了No.37+Ka螺旋桨系列，其结果都已绘制成Bp-δ型设计图谱可供应用。国内对导管螺旋桨的研究也相当活跃。中国船舶科学研究中心通过对2组6个不同剖面的导管与螺旋桨系列的敞水试验，研究了导管各种几何参数对导管桨性能的影响，并推荐了性能优良的导管螺旋桨系列。上海交通大学船舶流体力学研究室根据使用单位的要求简化导管的加工工艺，在系列研究基础上推荐了2组简易导管螺旋桨系列，即JD75+Ka螺旋桨系列和JD7704+Ka系列[1]。由于其加工方便，而性能又与机翼型导管相接近，故为不少单位所采用。

Fluent公司近年来推出的流体力学软件Fluent可广泛用于水流、气流、热流、化学反应、混合流，甚至固液混合反应的分析[2]，并有多种图文并茂的结果输出，非常适用于对导管性能的分析，并有可能用数值分析的方法，而不是试验方法对其尺度、几何参数等进行优化。这必将降低设计成本，提高工作效率。

由于本文所要应用的导管有特定尺度条件限制，上述文献提供的性能优良的导管并不能满足应用要求，故本文在优良导管形状的基础上选取几何参数，利用Fluent软件对其流场进行数值计算。并计算分析了在不同前缘收缩系数、后缘扩张系数、平行中体长度以及不同长径比条件下设计导管的推力系数、升阻比和流场分布等。最后通过以上的计算分析各参数对导管水动力性能的影响，从而挑选出满足条件的较优的导管形状。

2 导管的几何特征

由于所设计导管推进器主要用于低速时的推进，负荷比较大，根据导管螺旋桨特点，具有接近JD75导管几何特征参数的导管比较合适。

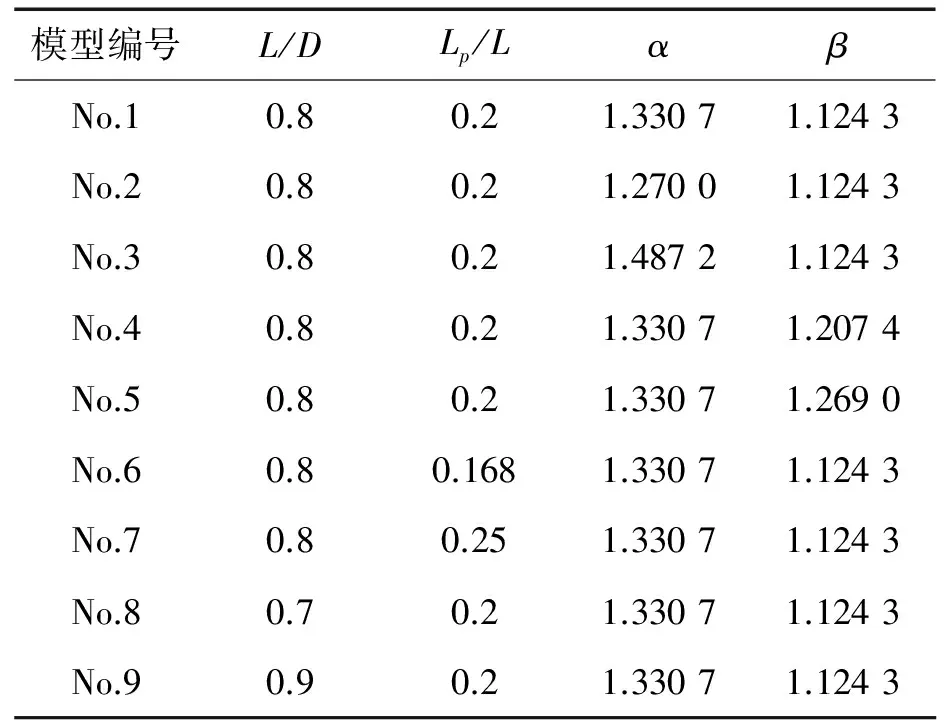
如图1所示，表征导管特征的几何参数主要有以下几个：长径比L/D、平行中体与导管长度比Lp/L、收缩系数α=A1/A0、扩散系数β=A2/A0(A1,A2,A0分别是导管相应位置的截面积)。为探讨导管几何形状对导管水动力性能的影响，选择JD75导管的几何参数作为参考，以一定规律变化L/D、Lp/L、α、β，生成系列导管。变化范围局限于前文提到的现有导管的几何参数，共计9个导管形状，参数见表1。

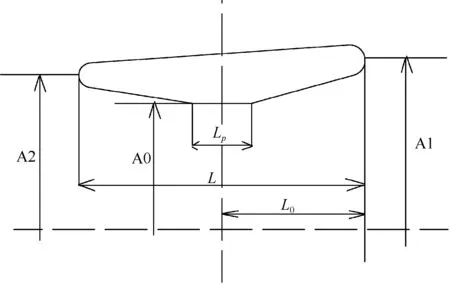
图1 导管剖面几何尺寸示意图

表1导管几何参数

模型编号L/DLp/LαβNo．10．80．21．33071．1243No．20．80．21．27001．1243No．30．80．21．48721．1243No．40．80．21．33071．2074No．50．80．21．33071．2690No．60．80．1681．33071．1243No．70．80．251．33071．1243No．80．70．21．33071．1243No．90．90．21．33071．1243

3 利用Fluent软件对导管进行数值模拟与分析

3.1 建模

以JD75导管几何参数作为设计基础，均取桨盘面距前缘距离与导管长度比：Lo/L=0.4，并取桨盘处直径为820 mm，建立模型A1，以此作为导管计算的参考标准。

A1模型参数如下：

长径比L/D： 0.8

平行中体与导管长度比Lp/L： 0.2

收缩系数α： 1.330 7

扩张系数β： 1.124 3

3.2 计算条件[3]

1) 根据相对性原理,假定导管静止不动,水流以一定的速度从前方流向导管，Va为流经导管的进速；

2) 计算区域

考虑到计算机的计算能力和计算模型的可靠性[4],计算域如图2所示。根据流场的对称性,二维计算只取导管剖面的一半进行计算，并在桨轴中心线的位置取对称条件。外轮廓线为计算边界，轮廓线之间是水流流动区域。为保证流场充分发展，长度方向导管的上游及下游分别取10L，高度方向导管外侧也取10L。

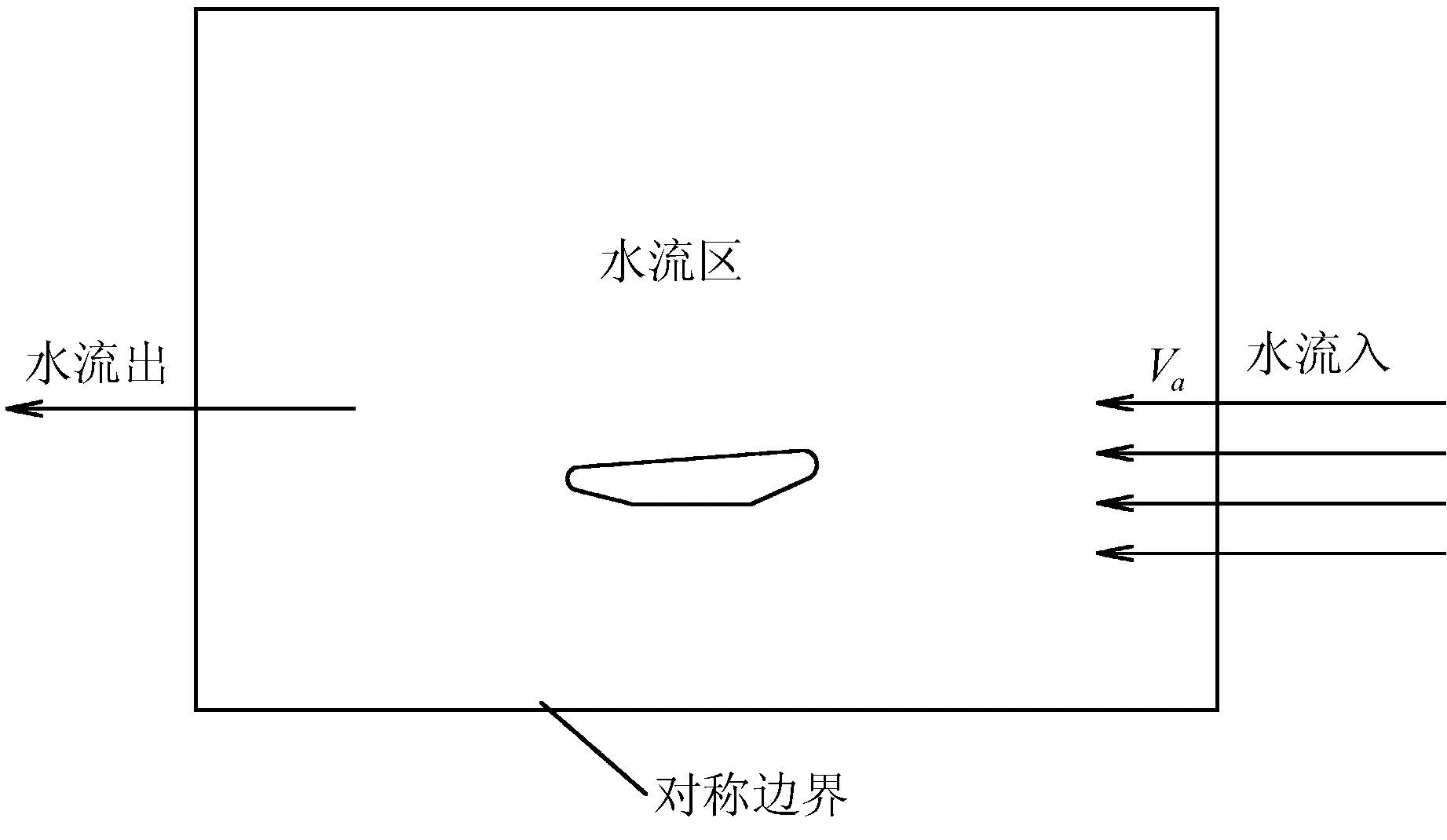
图2 二维计算域示意图

三维模型的计算域如图3所示。取一个包围四分之一导管的四分之一圆柱，其范围的选取与二维相仿。

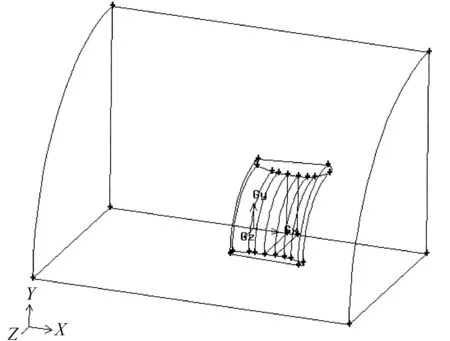
图3 三维计算域示意图

3) 边界条件

计算域的入口采用速度入口条件，即给定速度的大小和方向余弦。计算域的出口采用自由流出，导管表面采用固壁面条件，对称边采用对称条件。

4) 网格划分

理论上网格划分的越细,计算点距越小,计算效果越理想[5,6]。实际上Fluent主要用差分法和迭代法解N-S方程,计算精度受到计算机计算能力的影响,需要采取一个折衷的办法。本文的计算取近壁面边界层第一层网格高度为10-3倍的L，近壁处理采用标准壁面函数法，经计算检验其Y+值(Fluent中为了标识粘性底层与对数律层的分界点而引入的无量纲长度参数)可以控制在60以下，即保证了第一网格到壁面距离在对数区内。因为Fluent允许对称结构只算一半,故这样的计算精度既在个人计算机的计算能力允许之内,又能在总体上一定程度地准确反映出导管周围的流场情况。二维和三维网格划分分别如图4、图5所示。

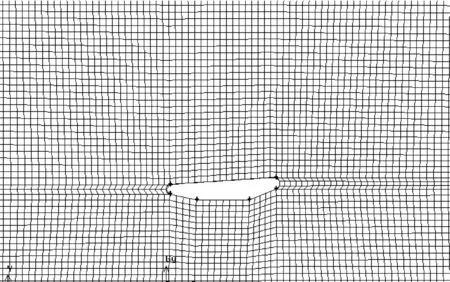
图4 二维模型导管周围网格

图5 三维模型导管周围网格

3.3 计算结果

通过计算，得到了二维模型的升阻比和三维模型的推力、推力系数和流场分布。图6为No.1导管切面沿弦长方向各点压力系数分布曲线。图中黑线为导管外表面压力系数，灰线表示导管内表面压力系数。图7是其中一个导管推力的试验结果与计算结果对比图，对比结果表明了计算方法的有效性。

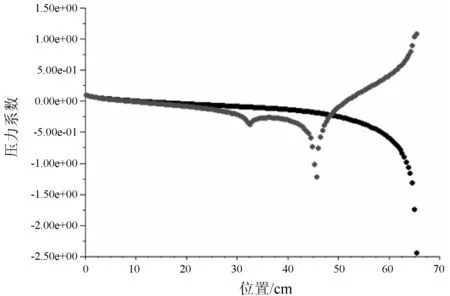
图6 No.1导管切面压力系数分布曲线

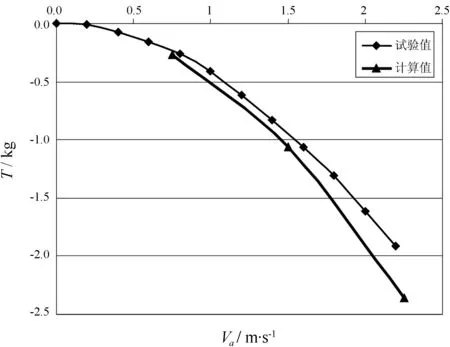
图7 导管推力的试验结果与计算结果对比

4 结果分析

在No.1模型的基础上，以一定规律变化L/D、Lp/L、α、β，生成系列导管，共 9个导管形状，其几何参数见表1。

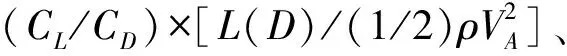
由图8知，在J=0.3(设计工况)附近，各个导管之间的升阻比关系如下：

1) No.3>No.2>No.1 (表明α的影响)

2) No.4>No.5>No.1 (表明β的影响)

3) No.7>No.1>No.6 (表明Lp/L的影响)

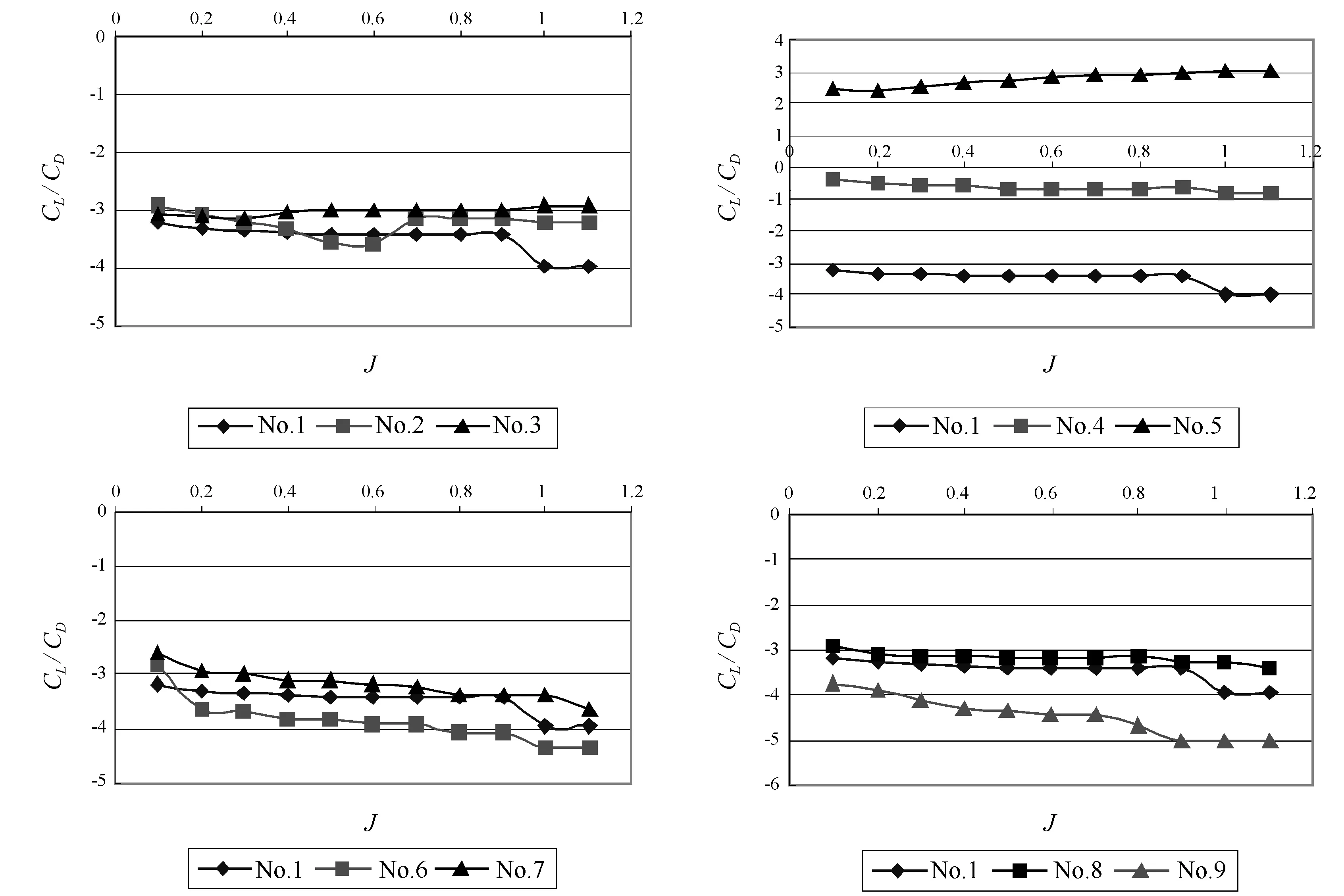
图8 模型No.1～No.9升阻比曲线图

图9 模型No.1～No.9推力系数曲线图

4) No.8>No.1>No.9(表明L/D的影响)

由图9可知，在J=0.3(设计工况)附近，各个导管之间的推力系数关系如下：1) No.2>No.1>No.3; 2) No.5>No.4>No.1; 3) No.1>No.7>No.6; 4) No.1>No.9>No.8。

由以上结果可以看出，在文献推荐的优良导管几何参数范围内，α越小，β越大导管所受阻力越小，L/D和Lp/L则是在取中间值时导管的阻力最小。再结合图8、图9中数值的变化幅度来看，虽然几何形状对推力系数KTD0有影响，L/D、Lp/L影响不是很大，α和β变化影响比较大。不同几何参数的变化对升阻比CL/CD是有影响的，但β变化影响最大。