基于Vega的虚拟海洋视景仿真研究

1 引 言

在视景仿真研究中虚拟自然环境的生成一直就是最具挑战性的研究方向之一[1]。由于自然环境的随机性和复杂性，使对其进行逼真地模拟十分困难，其中海洋环境的模拟更为复杂，因为在不同的情况下海洋的形态各不相同。海洋视景仿真的重点是逼真地模拟出海面的波浪起伏。对海浪的建模一般从三个角度出发：一是从物理的角度出发，通过求解流体动力学方程，对海浪内部各质点的运动加以描述[2]；二是从海浪的几何形状出发，采用三角函数和参数方程表示海浪曲面[3]；三是从海洋观测的结果出发，采用适当的海浪谱反演方法模拟海浪[4-6]。

本文以当前业界主流的高层软件环境——Vega作为开发平台， 系统研究了Vega环境中基于Longuet-Higgins海浪模型模拟三维动态海浪。

2 海浪模型

海浪研究是基于军事需要兴起的一个研究领域。海浪的形状时刻进行着不规则的变化，所以对海浪的模拟十分困难。50年代中期，将观测资料和液体波动理论结合起来模拟海洋，这带有很强的经验性。50年代初，海洋动力学家Pierson及Neummn等人用随机过程理论分析海洋，这种方法称为谱分析法。在此基础上人们提出了多种海浪模型，如Longuet-Higgins模型和Pierson模型。

2.1 Longuet-Higgins模型

该模型把海上一固定点的波面用多个随机的余弦波叠加来描述[7]：

(1)

式中，t为时间矢量；x为波点位置，通常x取0；εn为均匀分布的随机数，它在0～2π范围内出现在间隔α～α+dα的概率为:

(2)

式(1)中还规定:

(3)

我们考察量:

(4)

式中，ρw为水的密度；g为重力加速度。式(4)求和符号运算结果表示频率介于ω～ω+dω区域内组成波的能量之和，除以得δω此间隔内的平均能量。S(ω)代表海浪能量相对于组成波的频率分布，如果取δω=1，式(4)代表单位频率间隔内的能量，给出了能量密度，故S(ω)称为能谱；又因为它给出了能量相对于频率的分布，也称为频谱。

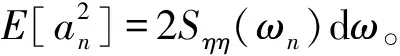
(5)

式中，Sηη为所需要模拟的海浪频谱，称为靶谱。

波数kn与圆频率ωn满足色散关系[9]，即：

(6)

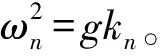
于是可得海面波浪方程:

(7)

式(7)的物理意义为:海洋上的不规则波浪，是由许多对应于波谱中各分量的振幅和频率的单元规则波组合而成，这些单元波的初始相位是随机的。

2.2 Pierson模型

Pierson参照Rice分析无线电通信中杂乱噪音的结果，将固定点的波面表示为部分和:

(8)

在频率轴上依次选取点ω0<ω1<…<ω2r+2，确定函数A2(ω)。读取A2(ω2n+1)的值，将此值乘以频率间隔ω2n+2-ω2n后开平方，得到的结果作为频率为ω2n+1、相位为随机量ε的余弦波的振幅，其中ε的分布仍为式(2)所示。可以看到，式(8)的含义为它代表多数随机余弦波的叠加。

2.3 Vega环境中海浪原理

虚拟海洋环境中有一个专门的海洋模块，它包括模拟海上运动所必须的一些特点，例如:动态和静态海洋模型中的动态学效果、域矢量特点以及海洋的特技效果等。海洋模块中包含动态和静态两个部分。宏观的海洋是静态的，静态海洋是静止不动的一个平面，上面赋予海洋的纹理帖图,也可以把观察者和静态海洋之间的海域定义为动态的，动态海洋由一些运动的面片构成，面片的运动规律遵循海浪的变化，面片上同样可以进行纹理帖图。图1为动态海洋和静态海洋之间的关系。

图1 动态海洋和静态海洋之间的关系

Vega海洋模块所使用的算法是基于Longuet-Higgins模型，用一个传播可变波浪模块以1:6的比例生成一个动态海景，观察者观察海洋状态，然后选择一个二维纹理用于三维的光滑波浪表面。创建一个真实波浪要用10条余弦曲线和一些非谐波频率，其中瞬间波浪高度可用下式计算[10]:

+Ωiωst+φi]

(9)

在浅水区摩擦力会影响波浪的传播速度;在深水区波浪的传播速度取决于它的重复周期。

(10)

3 海洋模块的计算机实现

3.1 海洋模块初始化

海洋模块需要为Marine、Oceans、Field Vectors、Marine Effect以及Special Effects类安装Vega类扩展名，调用函数vgInitMarine和vgInitFx对Vega海洋模块和特技效果模块进行初始化。以下代码表示为海洋模块进行必要的初始化。

main()

{ /* Initialize the Vega system */

初始化Vega系统

vgInitSys();

/* Initialize the Vega Marine module */ 初始化海洋模块

vgInitMarine();

/* Initialize the Vega Special Effects module*/ 初始化海洋特殊效果

vgInitFx();

/* scan the special .df file*/ 读取应用程序定义文件

vgDefineSys("mymarine.adf");

/* Configure the system and user define classes */ 实现系统配置

vgConfigSys();

/* real-time loop */

While 进入Vega主循环

{ vgSyncFrame();帧同步处理

vgFrame(); 当前帧处理

/* place application specific code here */ }

}

3.2 Marine类接口

海洋类为海洋模块的其他各类提供一个容器，对于一个应用程序只创建一个海洋类事件。与海洋类关联的是API函数是vgInitMarin和vgGetMarine，vgInitMarine函数初始化海洋模块，函数vgGetMarine返回海洋类事件。

3.3 海洋类接口

在海洋模块中，一个海洋事件定义波浪运动和观察者周围景物的外观，以及在一定距离内的海洋外观。每个海洋事件都有一个以观察者为中心向外扩散的动态效果，在较远距离处采用静态效果。由一个海洋事件可以参考多个海洋效果类型的Vega的类事件。图2表示Oceans的连通性。

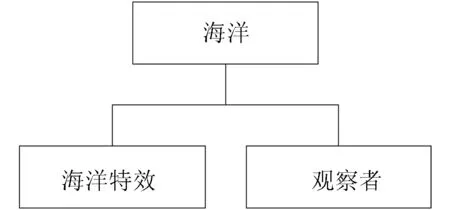
图2 Ocean的连通性

3.4 海浪生成效果图

由计算机生成的不同海况下的海浪效果图，图3为海浪周期4 s，海浪高度4 ft的海浪效果图；图4为海浪周期13 s，海浪高度19 ft的海浪效果图。

图3 浪高4 ft的海浪

图4 浪高19 ft的海浪

4 结 论

本文从对Longuet-Higgins模型和Pierson模型的讨论，重点研究Vega环境中海浪生成原理，并由计算机生成海浪效果图。海面波浪的计算机模拟比较复杂，Vega软件对海浪的模拟模块化，这使得模拟难度得到降低。同时，采用谱分析法反演生成的海浪能够真实地反映海浪的特性，并且生成的海浪效果比较真实，这为以后利用虚拟系统进行训练打下了良好的基础。

参考文献:

[1] 褚彦军,康凤举，聂卫东，等.海面场景虚拟仿真方法[J].计算机应用，2004，24(B12):114-117.

[2] 徐迎庆，苏成，李华，等.基于物理模型的流水及波浪模拟[J].计算机学报，1996，19(增刊):153-160.

[3] PEACHEY D R.Modeling waves and surfaces[J].Computer Graphics，1986,20(4) :65-74.

[4] 费华东,李伟青.基于网格计算的近海岸波浪仿真[J].系统仿真学报，2005，17(9):2142-2145.

[5] 黄兴忠，熊惠芳，李彦佐.一种改进的随机起伏海面的仿真方法[J].海洋学报，2006，28(6):151-157.

[6] 元建胜，贾俊涛，孟婵媛.海浪的动态视觉仿真[J].海洋科学进展，2005，23(4): 498-503.

[7] 文圣常.海浪理论与计算原理[M].北京:科学出版社，1984.

[8] 陶尧森.船舶耐波性[M].上海:上海交通大学出版社，1985.

[9] TESSENDORF J.Simulating Ocean Water[J].Proceeding of ACM SIGGRAPH，NewYork:ACM Press，1999:348-367.

[10] 龚卓荣.可选模块的使用与开发[M].北京:国防工业出版社，2003.