优化练习设计 激活学生思维
2007-10-20蒋寿桐
蒋寿桐
《数学课程标准》指出:“数学在提高人的推理能力、抽象能力、想象力和创造力等方面有着独特的作用。”小学生学习数学和解决数学问题的过程,是思维活动的过程,更是促进其思维发展的过程。因此,数学教学要遵循儿童的心理特点和认识规律,创设情境,引导探索,开放教学,发展学生的思维。
一、联系生活,创设情境,激发思维
数学来源于生活,学生的数学学习只有回归生活,才能深刻地理解数学,提高解决问题的能力。数学教学要从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,使学生获得对数学的理解的同时,在思维能力、情感态度与价值观等多方面得到进步和发展。在教学中通过问题情境的创设,让学生体验现实,身临其境地获得对知识的真实感受,从而激发学生的思维。
[案例1]李大爷要在他家的院子里用篱笆围一个鸡圈,已知篱笆的总长是24米,请你帮助李大爷设计一下,应怎样围鸡圈的面积才能尽可能大?面积是多少?
长方形和正方形的周长和面积的知识告诉我们:在周长一定的情况下,围成正方形面积比长方形面积大,所以绝大多数学生都认定要用24米的篱笆围成正方形鸡圈。
列式为:24÷4=6(米),6×6=36(平方米)。
至此,很多老师认为这道题目的教学已经结束,且答案也很圆满。我们认为上面做法只是一个抽象的数学模型,它来源于生活,但与生活实际有一定的差异,必须让数学模型回归生活并与实际应用相对比,在对比中去拓展学生的思维。
教学中我继续提出这样一个问题:如果利用李大爷家院子的院墙去围鸡圈,面积是否有可能扩大呢?
问题抛出后,我给学生留出“时间空白”,积极为学生提供讨论探索的机会,设法点燃学生心中的思维火把,努力形成教师与学生、学生与学生之间的思维互动,让学生自由发表意见。学生边讨论、边画图、边争辩,智慧的火花在思维激烈的碰撞中产生。
生1:院墙算一条边,篱笆作为另三边,围成正方形。
列式为:24÷3=8(米),8×8=64(平方米)。
生2:不对,院墙算一条边,我通过计算,64平方米不是最大的鸡圈,我设计出了更大的鸡圈:以院墙为一边,用篱笆围成另三边,围成长方形且长是宽的2倍时,其面积最大。
边说还边画图边列出算式:24÷2=12(米),12÷2=6(米),12×6=72(平方米)。
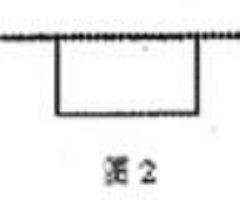
生3:我还有不同意见,我想李大爷家的院子不可能只有一堵墙,如果利用院墙一角去围一个鸡圈,面积更大。
他画出如下的图形,并说出了自己的算法:24÷2=12(米),12×12=144(平方米)
生4:如果院子足够大,院墙足够长,我以院墙为鸡圈的三边,可能会围出更大的鸡圈……
事实上,类似围鸡圈的问题在生活中经常遇到,教学中教师通过设计活动情境,让学生对数学知识的理解更深刻,体验更丰富,既激发了学生的思维,又培养了学生利用所学知识解决实际问题的能力。
二、提供条件,引导探索,促进思维
数学教学活动必须建立在学生已有的知识经验和认知发展水平基础之上。教师应激发学生学习的积极性,为学生提供充分从事数学活动的机会和条件,引导学生通过自主的探索和努力,获得成功,体验喜悦,真正使学生的学习过程变成一个不断创设问题情境,引起认知冲突,激发探求兴趣,训练思维品质的过程。
[案例2]学习了“长方体正方体表面积和体积”后,我设计了这样一道题来培养学生空间观念的建立,促进思维发展:从一个长5厘米,宽4厘米,高3厘米的长方体上,截去一个棱长1厘米的小正方体,长方体的表面积有怎样的变化?
我是这样引导学生进行探索的:
首先抛出第一个问题:在长方体上截去一个小正方体中“截去”该如何理解?
有同学说:截去,就是挖去、去掉。
接着我抛出第二个问题:有可能在什么位置上截?
问题抛出后,我启发学生打破思维定势,多角度地思考,鼓励他们发表不同的见解,让他们的创造欲在执著的追求中受到激发。他们通过动手摆一摆、画一画、比一比,在比较中发现新问题、新情况,产生新观点,在学生的集思广益中,发现有3种截法,即:
①从长方体的一个顶点上截去一个小正方体:
②从长方体的一条棱上截去一个小正方体:
③从长方体的一个面上截去一个小正方体。
“在长方体什么位置上截去小正方体”这一问题解决后,我抛给学生第三个问题:长方体的表面积有怎样的变化?学生的思维异常活跃,有些学生主动地去操作,有些学生在自己的作业本上计算、数着小正方体面的变化,其中好多同学还运用了平移、推理等一些方法,发现:
①从长方体的一个顶点上截去一个小正方体,长方体的表面积不变。
②从长方体的一条棱上截去一个小正方体,其表面积增加2个小正方形的面积。
③从长方体的一个面上截去一个小正方体,其表面积增加4个小正方形的面积。
题目研究完了,当学生还沉浸在探索的快乐中,体验着成功的喜悦时,我趁热打铁把题目中高3厘米改为1厘米,即从一个长5厘米,宽4厘米,高1厘米的长方体上,截下一个棱长1厘米的小正方体,长方体的表面积有什么变化?
学生再次投入到高强度的思维活动中,本题看上去与上题情况类似,都是在长方体面上截一个正方体,其实它们有着一定的区别,因为本题中长方体的厚度与小正方体的棱长相等。
即:①从长方体的一个顶点上截去一个小正方体,长方体表面积减少2个小正方体的面。
②从长方体的一条棱上截去一个小正方体,其表面积没有变化。
③从长方体的一个面上截去一个小正方体,其表面积增加2个小正方形的面。
这样的训练,活跃了学生的思维。加深了对知识的理解,同时让学生获得真切、丰富的学习经历,体验并感受着成功的快乐。
三、打破常规,开放教学,发展思维
学生的数学学习内容应当是现实的、有意义的、富有挑战性的。学生的数学学习活动应当是一个生动活泼的、主动的和富有个性的过程。开放教学有利于使学生形成合理的认知结构,有利于培养学生独立思考的习惯,有利于强化学生创新的动机,发展学生的思维能力。
[案例3]有一块长40厘米,宽20厘米的铁皮,用它做一只深5厘米的长方体无盖铁盒,要求容积越大越好,你准备如何设计?
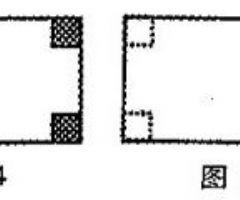
学生已有了长方体的表面积和体积的知识基础,因此我要求学生动手实践,用一张长40厘米,宽20厘米的纸进行研究,稍加点拨,学生很快得出:在其4个角上分别剪去一个边长5厘米的小正方形,再折叠成为一个长方体无盖铁盒。
求出容积为:(40-5×2)×(20-5×2)×5:1500(立方厘米)
这时教师引导:1500立方厘米是最大的容积吗?如果有顾客提出要充分利用边角料,有没有可能增加铁盒的容积呢?
学生的思维马上活跃起来并向深层发展,因为学生们知道利用边角料就是增加了原材料的可利用率,容积肯定变大,这是一个开放性的且对现实生活很有意义的设计,所以兴趣倍增。学生在自己充分挖掘图形自身的数据特点后,再次用手中的纸片进行操作,在操作中发现:把长方形铁皮两角上分别剪下两个边长5厘米的小正方形,焊接到长方形的另一条宽的中央,再折叠成一个长方体无盖铁盒。
其容积为:(40-5)×(20-5×2)×5=1750(立方厘米)
通过比较发现,这样设计比刚才的设计净增了250立方厘米,
这时学生思维完全被新的情境所激活,数学思维得到充分的锻炼和发展。
总之,在课堂教学中,我们要致力于把学生从枯燥的题海中解放出来,把重心放在引领学生探究数学的奥秘上,鼓励和帮助他们在广阔精彩的数学世界里自由翱翔,获得持续发展的学力。对同一个学习内容,要引导学生多层次、多角度、多侧面进行分析推理,引导学生动手实践、合作探究,经历知识的发生和发展过程,使学生的思维得到生动活泼的发展。
(作者单位:淮安市新安小学)