特定的舰船维修任务分配问题研究

翁 辉 胡德生

海军工程大学管理工程系 武汉 430033

特定的舰船维修任务分配问题研究

翁 辉 胡德生

海军工程大学管理工程系 武汉 430033

分析战前舰船维修任务的特点，并对相关因素进行了简化，按照不同的任务需求，建立了任务模型和维修方案模型，并结合运筹学的线性规划问题和任务分派问题，给出舰船维修任务分配问题的求解方法和过程，最后用实例进行引证。

任务分配问题 舰船 维修 模型

部队在战前都必须对舰船装备进行临时抢修，任务量大，时间紧，保障单位的资源相对有限。舰船抢修计划安排是否得当，不仅直接影响维修经费的合理使用，而且也直接影响到舰船的在航率和战斗力［1-2］。

1 战前舰船维修任务分析

舰船维修任务的安排涉及到的因素很多，通过分析，可以将这些因素归纳为两大类。一类涉及到舰船本身，一类涉及到维修保障单位。

舰船本身的维修因素包括舰船类型、数量、修理等级、维修时限、维修时间、维修的优先权值、目前位置、执行任务位置、装备的性能参数等。有关保障单位的维修因素有：舰船保障单位的位置、维修能力、设施承修能力、技术保障力量信息、在修舰船情况、其它因素。由于舰船的种类较多，型号不一，船体、机电设备各不相同，吨位相差很大。而又限于自身的设施设备和技术保障力量，舰船维修单位的能力各不相同。因此，在进行任务分配过程中，管理人员除了解舰船的总体保障任务外，还需要了解舰船自身情况、保障单位基本情况。要合理地进行任务分配，是比较困难的。

舰船维修任务分配涉及的因素较多，因此，必须对这种分配的问题进行合理的简化，以便用数学方法来分析和求解问题。

1）对舰船的类型进行简化，鉴于部分舰船的船体、机电装备等相同或类似，因此对舰船的类型进行缩减，并且此种分类适用所有的维修保障单位。

2）要考虑到不同类型舰船的维修优先权（即急需修理的，时间要求紧的，按照在作战中担负的任务而言，特别是指在任务不能完成的情况下，应优先保证哪些舰船得到修理）。

3）维修单位的因素：在单位对舰船（按照舰船类型）维修能力的确定下，假设保障单位的维修能力（分配的数量）只与其设施有关，与其它的技术保障力量等无关（可认为在战时其它的技术力量能够实施机动保障）。每个单位的设施资源是有限的。

4）维修单位的维修能力方案是指根据现有设施，同时进行分配和维修的能力。考虑到维修单位的综合效益与军事需求，能力方案可能有多种。

2 建立舰船维修任务模型和单位维修方案模型

2．1 舰船维修任务模型

根据对舰船维修任务的合理简化，我们不妨首先列出维修任务，假设舰船的种类为（T1，T2，T3，…，Tn）共n种，其待修的数量为（S1，S2，S3，…，Sn），维修的优先权值为（C1，C2，C3，…，Cn），可以用表1的方式将维修任务表达出来。

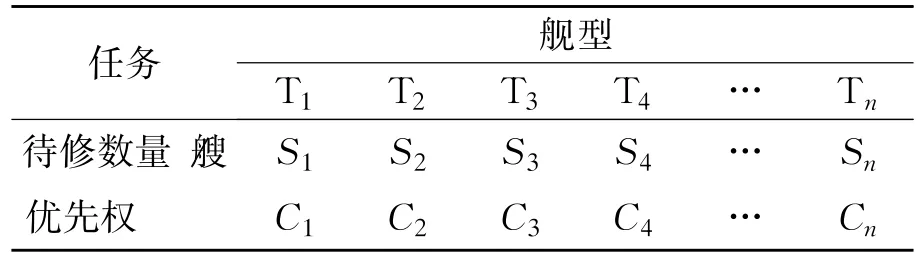
表1 舰船维修任务表

2．2 保障单位的维修方案模型

每个单位综合自身的设施设备情况、技术力量情况以及已往承担的任务信息，可以提出一种或多种承修方案，在每种方案下，没有多余的资源对保障舰船进行任务分配，而且每种方案都既能保证部队的军事需求，也能保证单位获得较大的经济效益。根据这个假设，可以用一个矩阵（本文称为单位能力矩阵）来表达单位的承修方案

式中：——在k单位的承修方案m中可以维修Tn种舰船的数量。

2．3 总的任务分配方案模型

如果所有的单位都参与任务分配，按照最悲观的打算（即任务量太大，每个单位必须都有维修任务），可能的分配方案有

式中：mk——第k个单位的承修方案总数；

l——参与任务分配单位的总数。

那么可以用一个矩阵Az来表示总的可能分配方案，如下式

矩阵右边指由由各个单位的哪些能力方案相加，左边对应为这些方案相加后的值。如12，21，31，…，l1表示单位1的方案2加上单位2的方案1加上单位3的方案1，一直相加到单位l的方案1，相加得到的结果为S2，1，S2，2，…，S2，n。这个矩阵中含有所有可能的任务分配方案，如何求出其中的最优或满意解，必须根据具体的情况对这个矩阵进行分析和处理。

3 舰船维修任务分配问题求解方法和步骤

根据2．3可知，总的分配方案都含在Az中，是否存在最优解，就需要与任务矩阵进行比较。为此，特构造一个任务矩阵B，矩阵的行数与Az相同，见式（4）。

3．1 存在最优解

如果存在最优解，也就是维修能力能够满足舰船的维修任务，不存在有的任务无法完成的情况，根据上述分析，可以按照下述求解过程进行求解。

3．1．1 步骤1

先用矩阵Az减去标准矩阵B，得出一个新的矩阵Az（—），见式（5）

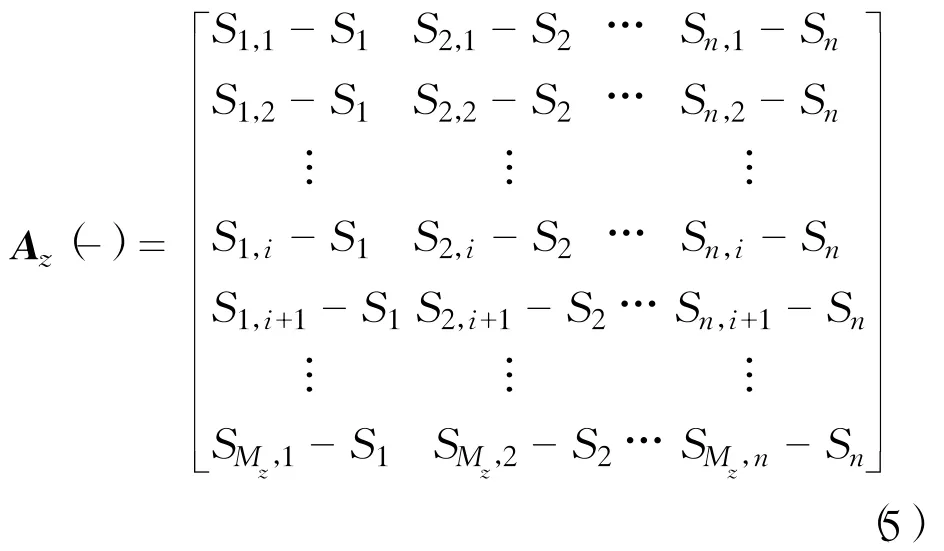
3．1．2步骤2

对矩阵Az左边中的每一行进行判断，如果存在一行中所有的值都大于或等于0，那么这行右边所代表的分配方案即为最优解。具体分配时，如果此行中所有值都等于0，即证明在此种分配方案下任务刚好能够完成，在数量上按照各个工厂标称的能力去分配。若此行中存在大于0的值，那么此值所在列所代表的舰船维修任务是能够完成的，且工厂的维修能力过剩。因此，在按照数量分配方案上至少有两种最优解。先按照各工厂能力方案中所标称的维修数量进行分配，再对维修能力过剩的此型舰船数量进行调整，使此型舰船的分配总数量与任务数量相同。

3．2 不存在最优解

任务量超出了所有保障单位的维修能力，也就是有的舰船维修任务无法进行安排，即不符合步骤2的条件，我们可以根据任务的具体情况来进行分析并求出满意解。

3．2．1步骤3

如果舰船维修任务对不同类型舰船的维修是强制性要求，不能用数值来描述其优先的高低，也就是说C1、C2、C3、…、Cn无法用于计算，只能够比较。例如维修任务是必须优先确保T1型舰船的维修，其次保证T2型舰船的维修，那么就可以按以下的方法去求解满意解。

假设C1≥C2≥C3≥…≥Cn，那么在矩阵Az（—）中，按照舰船类型权值的高低依次进行判断。先判断T1舰船类型。先得出第一列中值大于或等于0的所有行H1，或如果不满足此条件，则得出第1列中最大值的所有行H1；再从行H1中进行判断，得出第2列中值大于或等于0的所有行H2，或如果不能满足条件，则得出第2列中最大值的所有行H2；再从行H2中进行判断，得出第3列中值大于或等于0的所有行H3，或如果不能满足条件，则得出第3列中最大值的所有行H3；依次类推，一直到从行Hn—1中进行判断，得出第n列中值大于或等于0的所有行Hn，或如果没有满足条件，则得出第n列中最大值的所有行Hn，行Hn中涉及到的分配即为此问题的满意解。若在行Hn中存在大于0的值，其分配方法参考步骤2。

3．2．2步骤4

如果任务中舰船维修任务的优先值可以用数值进行衡量，那么分配问题可以转化为一个运筹学的线型规划问题［3］。

式中：Si——Ti类型舰船总数量。

z的理论最大值Z0是已知的，即

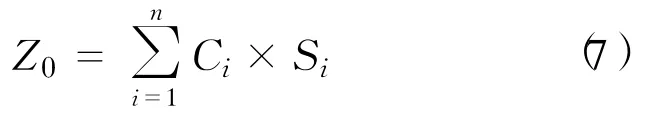
规定Δz＝Z0—z，Δz可以在矩阵中比较容易求出，因此只要求出Δz的最小值，便得出目标函数最大值。

根据要求，可以对矩阵Az（—）作进一步处理。规定矩阵Az（—）中所有大于0的值，都等于0。其它值不变，这样得到一个新的矩阵Az（—）′，再对矩阵Az（—）′作相应处理得出矩阵G，并从中求出min（ΔZ），其所对应的行就是分配的满意解，见式（8）。

式（8）中规定：当S≥0时，f（S）＝0；当S＜0时，f（S）＝S。如果此解中某型舰船的分配数量大于任务量，即单位对此型舰船的维修能力过剩，分配方法参考步骤2。

3．2．3 步骤5

如果维修任务对某型舰船而言，是强制性要求，而对其它类型的舰船的维修优先权值是可以量化的。例如：在确保Ti型舰船能够维修的情况下，按优先权值的高低安排其它类型的舰船进行维修。在这种情况下，各型舰船的优先值可表示为

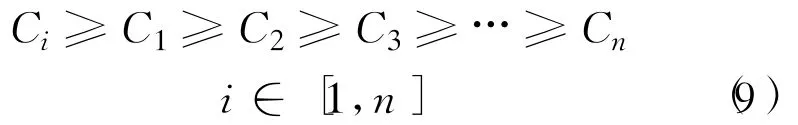
在这种情况下，应首先保证Ti型舰船的维修任务，解决方法如下：在矩阵Az（—）′中，先判断Ti型舰船，得出第i列中等于0的所有行Hi，或者如果不能满足此条件，则得出第i列中最大值的所有行Hi，然后从Hi中进行处理，后续分配方法参考步骤4。

3．2．4步骤6

如果维修任务对某些类型舰船是强制性，而其它类型的船只的维修优先权值是可以量化的，解决的方法原则是先解决强制性的，再解决优先权值可以量化的，参考步骤3和步骤5。

4 实例

4．1 实例1——维修任务能够完成

舰船的维修任务量见表2，假设有3个维修单位，其维修方案见式（10）所示。

表2 维修任务量

根据求解步骤1、2可求出最优方案分配方法为122132。此分配方案中部分舰船的分配数量超过了任务量，在具体分配时可以对这型舰船的分配数量进行缩减调整，使其总数与任务量一致。

4．2 实例2——总的任务量不能完成

维修任务量见表3，单位维修方案同实例1。

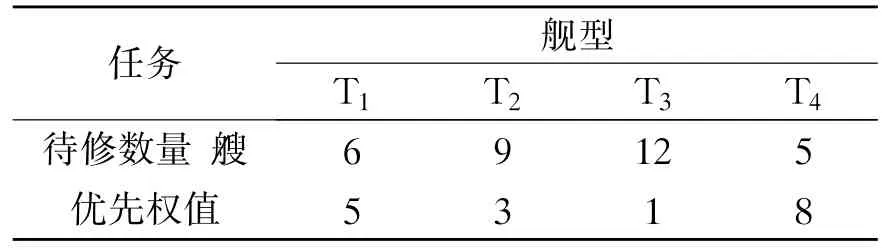
表3 维修任务量

根据求解步骤1、2得知在矩阵Az（—）中不存在最优解，由于各型舰船的权值可以进行计算，由此根据步骤4，可以得出其满意解为122132和

132132，故其分配方案有两种。分配方案中部分舰船的分配数量超过了任务量，在具体分配时可参照实例1。

4．3 实例3——维修任务分主次

在实例2中，由于作战任务的需要，必须首先保证舰型T1的维修，其次是保证舰型T2的维修，其它舰型的维修可以参照设定的优先权值。

分析题目可知，舰型T1和T2的维修是强制性要求，且舰型T1更优于舰型T2。根据求解步骤1、2和6，可以求出minΔZ＝3，其对应的方案为132132，即此方案为满意解。其具体的数量分配方法参考实例1。

5 结束语

战前舰船抢修任务繁重，维修任务分配涉及因素非常多，文中的方法，较好地解决了舰船维修任务的一次分配问题。在求解过程中，对一次分配中所涉及的因素如维修时间、维修地点、舰船驻泊地点、单位维修设施的二次利用等进行了简化，而在实际的任务分配过程中，由于各种舰船维修时间不同，故存在维修单位设施的重复利用的问题。如何更加科学合理地进行任务分配，还有待于进一步的研究。

［1］王肇基，鲍承昌．海军舰船修理计划决策支持系统［J］．中国修船，1998（1）：44-5．

［2］濮怀宇，张怀强．舰船装备修理规划方案的DEA分析与优化［J］．海军工程大学学报，2004（1）：67-68．

［3］顾基发．运筹学［M］．北京：清华大学出版社，1990：12-13．

Research on the special assignment problem of maintenance for warship

WENG Hui HU De-sheng
Dept．of Management Engineering Naval University of Engineering Wuhan 430033

The assignment problem of the warship maintenance is analyzed and simplified．According to the task requirements，the task model and maintenance model are built．Thesolution method and progress of theassignment problem by applying the theory of linear programming and assignment problem in the OR（operational research）are proposed with practical examples．

assignment problem warship maintenance model

TP315

A

1671-7953（2007）02-0114-04

2006-09-15

修回日期2006-10-16

翁 辉（1975—），男，硕士，讲师。