边界和长度对管节点附加水质量的影响

姬广令 于国友

天津大学建工学院 天津300072

边界和长度对管节点附加水质量的影响

姬广令 于国友

天津大学建工学院 天津300072

运用三维边界元方法，通过数值计算，证明在一定条件下流体边界、构件长度对管节点附加水质量均存在较大影响，以方形和圆形构件为例，分析构件附加水质量受这些因素影响的变化规律。

附加水质量 边界元 管节点

结构振动特性除受其刚度影响外，与其质量也存在着很大关系［1］。所以，准确地计算附加水质量对于分析构件在水中的运动规律具有重要意义。理论推导只能给出无限流场内无限长孤立柱体的附加水质量［2］，而实际生活中的流体及位于其中的构件均存在边界和其它构件的影响。

导管架平台早已被广泛应用于海洋工程中，其所受波浪力历来受到人们的重视。但目前广泛应用的仍然是仅适用于孤立柱体的Morison公式。由于交叉管线间的相互影响，此公式直接应用到管节点处肯定会造成较大误差，且导管架中为数众多的管节点的综合作用必将对其波浪力计算产生不可忽视的影响。然而，到目前为止管节点所受波浪力计算方法研究尚未受到应有的重视，但这并不说明其影响不重要。虽然有些学者建议将导管架所包围流体作为一个整体来考虑，但未给出具体计算方法。以一边长10．00 m正方形平面桁架（导管架）为例。如所有管径均为0．60 m，且仅在四个角点处存在管节点并有一根斜撑以保持稳定性［3］，则受3．5倍管径（2．10 m）内其它管线影响的管件总长度为23．76 m，占管件总长54．10 m的43．92%。如在最上面管件再设一管节点（将一根斜撑换成两根较短斜撑）以加强强度，则受3．5倍管径内其它管线影响的管件总长度为38．81 m，占管线总长62．40 m的62．20%。从中可见管节点影响的重要性。所以非常有必要总结出一套计算管节点所受波浪力的经验公式，至少是计算管节点水动力系数的公式。

波浪力中的群柱效应早已引起人们的注意［4-5］。经对两个顺流方向前后布置的圆柱的实验结果表明，当两圆柱中心距小于3．5倍圆柱直径时曳力系数较单柱时有较大差异［5］。Chakrabaki等人分别将2个、3个和5个柱体矗立在波浪水槽中，排成一列进行试验［6］。结果表明，当相对间隙（柱间距／柱径）小于1．3时，惯性系数和曳力系数增加惊人。五柱排列时，相对间隙从1．3变到

1．1，阻力系数将加倍。

总之，复杂结构附加水质量的计算方法与简单构件常常存在较大差别，应该引起理论界与工程界的普遍重视。

1 数值方法

1．1 数值模型

假设流体为势流，采用边界元法求解［7］。对于三维位势问题，控制方程为Laplace方程

对于任一点q，相应的边界积分方程可写成

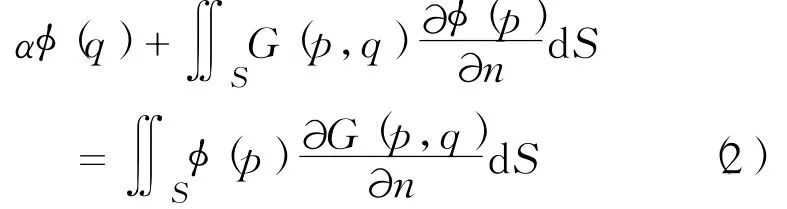
对于三维问题，式（2）的基本解为

式中：r——作用点p至观测点q之间的距离函数。

α的取值与边界光滑度有关，一般可用刚体位移等方法间接求解［8］。

为简化起见，离散化的方程（2）可以改写成

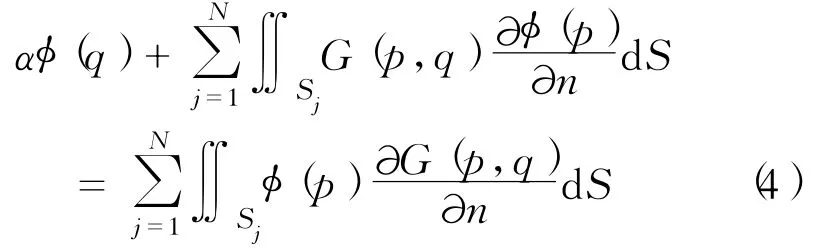
式（4）经整理后可用矩阵形式表示为

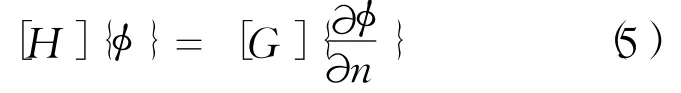
根据边界条件整理，将上式中的已知项移到方程的右边而将未知项移到方程的左边，可得

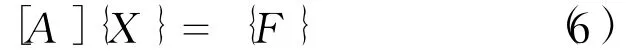
求解方程（6）即可得出边界上的未知量。

1．2 边界条件

为了简化起见，未考虑由于波动而引起的水面变化，即水面将始终保持水平，所以水表面处伯努利方程可写成

为了摆脱速度的非线性项的影响，仅考虑初始时刻，即水表面v＝0，且认为附加水质量与水的速度大小无关。则由方程（7），水表面的边界条件可写成

由于本文仅研究由于水的加速度而产生的附加水质量，且认为构件尺寸与海水深度相比很小，所以选取离构件足够远处水域的边界条件为

海底的边界条件为

1．3 数值处理

由于边界条件均与速度势对时间的导数有关，所以需要将方程（5）和（6）对时间求导。

式中：｛Y｝，｛T｝——｛X｝和｛F｝对时间的导数。

将方程（13）沿构件表面积分可得水体对构件的作用力

此力与构件作用在水体的力大小相等，方向相反。

2 实例分析

2．1 流体边界的影响

以方形和圆形构件为例，计算流体边界和管节点对其附加水质量的影响。流体计算区域及管节点尺寸见图1。

图1 流体计算区域及管节点尺寸

计算区域为40．00 m的立方体，即选水深40．00 m的正方体区域。方形构件边长均为1．00 m，圆形构件直径都为1．00 m，交叉构件为两个构件正交的倒T形，水平构件长9．00 m，竖向柱体高4．00 m。构件在y轴负方向作匀加速直线运动，加速度a＝1．00 m／s2，在z轴方向d从1．00 m开始变化，到34．00 m。计算时采用边界元方法，选择八节点等参元，流体外边界单元边长为40．00 m，共600个单元；方形管节点构件内边界单元边长0．25 m，共864个单元；圆形管节点构件内边界边长0．50 m，共995个单元。构件单位附加水质量随d的变化趋势见图2。

管节点有4．00 m的高度，其d以水面和水平构件中心为水深，从5．00 m开始。

由图2可看出，构件的单位长度平均附加水质量在自由面和水底附近变化较快。与理论值相比，水底附近的单位长度附加水质量偏高，而自由面附近偏低。在中间位置单位附加水质量变化平缓，与理论值较接近。方形构件管节点比圆形构件管节点的单位附加水质量要大。

为了比较管节点不同构件间的相互影响，图2中同时给出了方形和圆形水平构件单位长度附加水质量随水深的变化趋势。通过比较可以看出，交叉构件中的管节点各构件间的相互影响很大，构件的单位长度附加水质量比水平构件大很多。因此在计算物体附加水质量时，应该考虑自由表面或水底及管节点的影响，尤其是管节点的影响。

2．2 构件长度变化的影响

为了分析构件长度对其附加水质量的影响，将上例中的管节点分别换成孤立的水平和竖向构件。在分析孤立构件附加水质量的大小时，使构件中心始终与分析流体区域的中心重合，构件的长度从1．00 m变化到21．00 m。计算所得单位长度的附加水质量变化见图3。其中孤立的水平构件引起的单位长度平均附加水质量随构件长度的变化规律和大小与孤立的竖向构件基本一致。

图2 水平构件及T-节点单位长度平均附加水质量随水深的变化趋势

图3 单位长度平均附加水质量随构件长度的变化趋势

由图3可以看出，单独计算孤立构件时，单位长度平均附加水质量随着长度的增加而增大。当构件很短时，这种变化尤为明显。随着构件长度的增大，单位长度平均附加水质量趋于常数。方形构件由于边界效应的影响，其变化不如圆形构件明显，长度对圆形构件的影响更明显。

2．3 管节点对附加水质量的影响

在例2．1所述模型中保持d＝15．00 m及竖向柱体长度4．00 m不变，而使水平构件的长度从1．00 m变化到21．00 m，分析此时引起的管节点单位长度平均附加水质量的变化规律见图4。

图4 水平构件长度对管节点单位长度平均附加水质量的影响

由图4可以看出，当水平构件长度较小时，水平构件长度的增大对管节点单位长度附加水质量的影响较大，即使管节点单位长度附加水质量与孤立构件的差别增大。而当水平构件的长度达到一定值后，其长度的增大对此差别的贡献逐渐减小，并使此差别最终趋于常量。这说明管节点的影响仅限于其周围一定范围内，而在此范围外，其影响可以忽略。管节点对于圆形构件的影响比方形构件要大，这是因为方形构件有边界效应的影响，可以抵消一部分管节点的影响，但是在长度很小的情况下，管节点的影响也是不能忽略的。总之，管节点在构件长度较小时对构件的附加水质量是不可忽略的。

3 结束语

通过算例可以看出在一定条件下流体边界、构件长度对管节点附加水质量具有较大影响。

1）与理论值相比，水底使附加水质量增大，而水面使管节点附加水质量减小。

2）由于实际工程中的构件均为有限长度的三维构件，其附加水质量的大小一般均小于基于二维理论分析所得构件附加水质量值。单位长度平均附加水质量随着长度的增加而增大，且这种变化在构件较短时很明显。当构件长度较大时，其附加水质量将趋于二维理论分析值。

3）与单独构件相比，管节点使附加水质量增大。管节点的影响在一定范围较大，而在此范围外，其影响可以忽略。

由于本文仅着重于研究附加水质量的变化规律，故选取了40 m的正方体流体模型，不免会对精度有一定的影响。为了获得更精确的结果，建议选取更大流体模型。

最后，本文未考虑波动引起的重力波液面变化造成的影响［9-11］，所以其结果仅适用于小振幅波动问题。

［1］唐友刚．高等结构动力学［M］．天津：天津大学出版社，2002．

［2］王家楣，张志宏，马乾初．流体力学［M］．大连：大连海事大学出版社，2002．

［3］李润培，陈伟刚，顾永宁．近海固定平台碰撞的准静态分析［J］．海洋工程，1995（2）：14-21．

［4］李玉成，王凤龙，康海贵．作用于小尺度圆柱上的波浪、水流力［J］．海洋工程，1993（3）：42-49．

［5］徐继组，李维扬，王克让．海洋工程结构动力分析［M］．天津：天津大学出版社，1990．

［6］李远林．近海结构水动力学［M］．广州：华南理工大学出版社，1999．

［7］申光宪．边界元法［M］．北京：机械工业出版社，1998．

［8］嵇 醒，藏跃龙，程玉民．边界元法进展及通用程序［M］．上海：同济大学出版社，1997．

［9］Grilli S，Svendsen I A．Corner Problems and Global Accuracy in the Boundary Element Solution of Nonlinear Wave Flows［J］．Engineering Analysis with Boundary Elements，1990，7（4）：178-195．

［10］Grilli S，Skourup J，Svendsen I A．An Efficient Boundary Element Method for Nonlinear Water Waves［J］．Engineering Analysis with Boundary Elements，1989，6（2）：97-107．

［11］Grilli S，Skourup J，Svendsen I A．The Modeling of Highly Nonlinear Water Waves：A step toward a Numerical Wave Tank［C］．Southpamton，England：10th Intl．Conf．on Boundary Elements，Berlin：Computational Mechanics Publication．Springer Verlag，1988：549-564．

Numerical analysis of added mass on the T-joint by 3-dimensional BEM

JI Guang-ling YU Guo-you
Department of Ocean Engineering School of Civil Engineering Tianjin University Tianjin 300072

Through numerical examples by 3-dimensional boundary element method（BEM），it′s proved that the fluid boundary，the member length may also have great effects on the value of the T-joint added mass in many cases．The effects of these factors are analyzed in this paper through examples with square members and circular members．

added mass boundary element method T-joint

U661．71

A

1671-7953（2007）02-0009-04

2006-09-08

修回日期2006-10-29

姬广令（1984—），男，硕士生。