舰艇电力系统生命力评估中的图论分析法
2007-01-28
海军工程大学 船舶与动力学院 武汉 430033
电力系统是舰艇系统的重要子系统,提高电力系统的生命力,可大大提高整个舰艇及其重要设备的生命力。以电力系统生命力的整体评估为重点,探讨了图论方法的思想、计算及应用。并以某舰电力系统生命力评估为例,通过分析计算,对其电力系统的设计提供参考。
在研究系统可靠性问题时,经常采用故障树分析法,但是,采用故障树进行建模计算,并没有精确地反映系统的实质。因为,“树”只能用在分层系统,即同一层的元素是独立的,没有很大联系的,一般的系统仅用树并不能精确地描述系统的构成;而图,不仅能反映出层与层之间的隶属关系,还能反映出同一层元素之间的联系。研究电力系统的生命力,主要是研究其损伤的可能性,计算其损伤的概率。基于这种想法,在评估电力系统的生命力时,采取了图论分析法。
图,由一些点及一些点之间的连线组成。点是指某系统中的设备或元素,而线是指设备或(元素)之间的关系。图论分析法就是利用图论的知识和研究方法对系统的生命力进行分析。该法的关键是建立模型,即根据舰艇系统的设计方案或实物,分析其战斗环境,预测其损伤的各种可能,利用可靠性数学手段,建立损伤图模型,计算各设备的损伤概率,最后进行电力系统生命力的评估。
1 模型的建立
1.1 系统的组成
舰艇电力系统是由发电、配电和用电设备组成。从设备角度说,舰艇电力系统是由发电机及其控制设备、主配电板、配电中心、分配电板、传输电缆和电力负荷等组成。研究的目的是保证主要用电设备供电的概率,因此,在研究舰艇电力系统生命力时,将电力系统分成电站、主配电板、配电中心和传输电缆四大部分。电站应向作战系统、电力机构和所有用电设备提供所需的电力,是电力系统的心脏。
1.2 电力系统供电图
某舰电力系统有前后两个电站,每个电站配有两套柴油发电机装置和一块相应的主配电板,两个电站互为备用,一个电站可以满足全舰所有用电设备的供电需要所有负载都可以分别从两个电站得到两路供电,两个主配电板之间装有两根跨接电缆,两根跨接电缆互为备用且沿两舷分开布置。原理见图1。
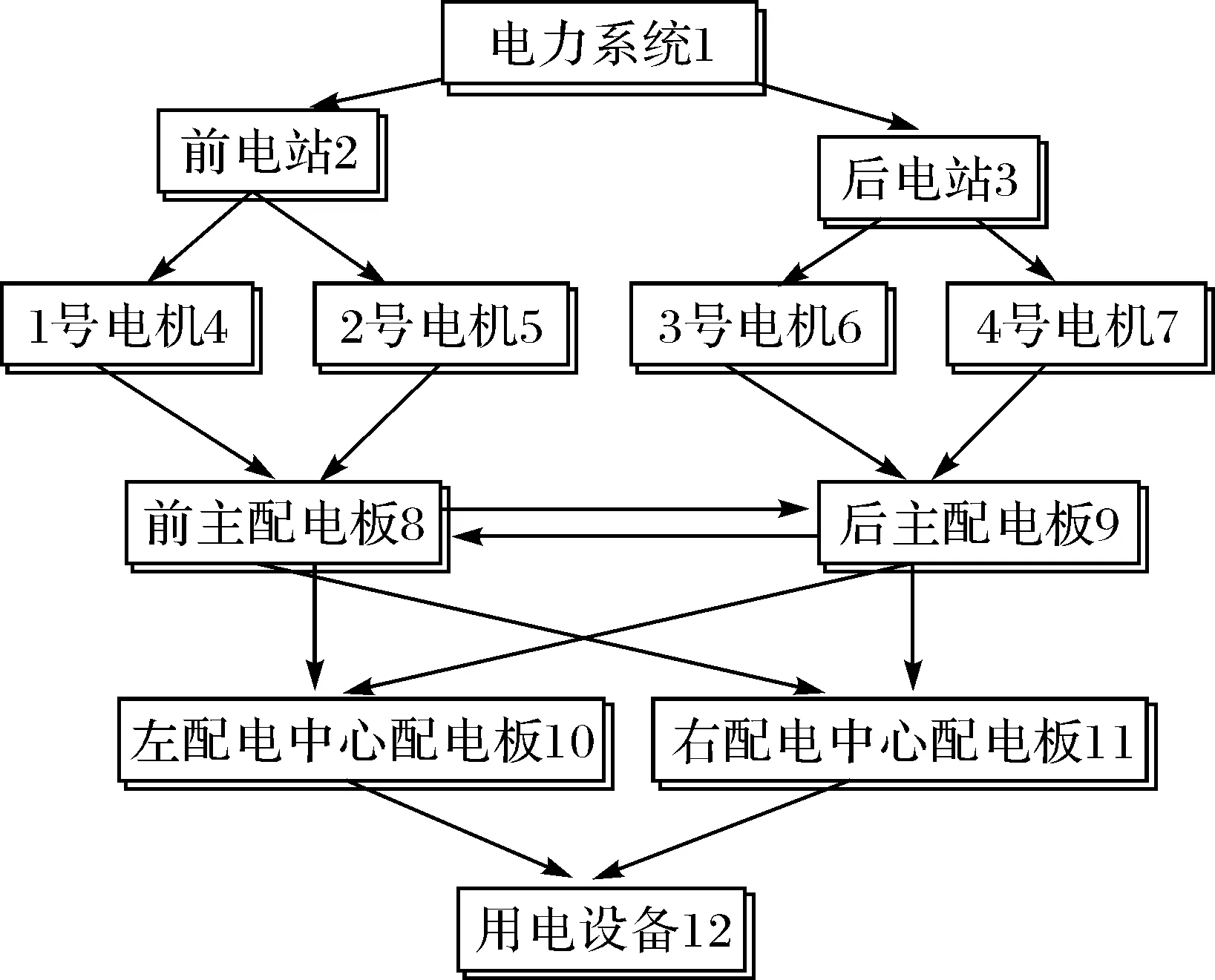
图1 某电力系统原理
1.3 电站的图论模型
假设电力系统中的每个设备或设施为一个节点,由上至下分别编号为1、2、……、12,(如图1所示)可将图1转变为图论中的图。
1.4 电站供电的生命力的定义
按主配电板的供电情况即电力系统供电率来划分电力系统的生命力等级。在确定电力系统生命力等级时,主要是根据电力系统的生命力等级与全舰的生命力等级相适应。
设系统的操作状态集为:S={A,B,C,D},A、B、C、D依次代表电力系统生命力的四个等级。
A级:完全丧失生命力。电站完全损坏,负荷供电率<5%,其反事件为:有一台以上的电机可以对设备供电;
B级:基本丧失生命力。电站供电率仅有50%,80%以上的分区配电板损坏。电力系统只能保证照明、通讯等供电,其反事件为:有两台以上的电机可以对设备供电;
C级:基本具有生命力。电力系统供电率高于50%,尤其要保证动力、武备、观通、导航等重要负荷的供电,其反事件为:有三台以上的电机可对设备供电;
D级:完全具有生命力。电站具有100%的供电能力,电力系统的供电率高于85%以上,重要负荷不失电,其反事件为:四台电机可同时对设备供电。[1]
1.5 电力系统的数学模型
定义1:对于任意图G,V为其节点,e为其连线,若存在W=v0e1v1e2v2……ekvk,且ei与vi-1、vi相关联,则称W为图G的一条道路,v0为W的起点,vk为W的终点,vi为道路的内点[2]。
定义2:G1,G2为两个图,且V(G1)V(G2),E(G1)E(G2),则称G1是G2的子图,记为G1G2。[4]
记图G所有子图分别为G1,G2,……,Gk,……,并记:
w1={w|w=w(v1,v12),且存在内点v4},
w2={w|w=w(v1,v12),且存在内点v5},
w3={w|w=w(v1,v12),且存在内点v6},
w4={w|w=w(v1,v12),且存在内点v7}。
根据图论知识,电站生命力的等级如下。
A级:G的子图的集合HA={H|HG,H不存在w1,w2,w3,w4中的任何一条道路} ;
B级:G的子图的集合HB={H|HG,H不存在w1,w2,w3,w4中的一条道路};
C级:G的子图的集合HC={H|HG,H存在w1,w2,w3,w4中的两条或三条道路};
D级:G的子图的集合HD={H|HG,H存在w1,w2,w3,w4四条道路}。
定义3:概率空间Ω={z|z=(x1,x2,……x12),xi=0,1;i=0……12}[5],任一事件z=(x1,x2,……,x12),对于图来说,每个节点的状态对应于一个xi,且
对于事件z=(x1,x2,……x12)来说
(1)
设有一事件集合T={z1,z2……zk……},且所有事件都是互斥,那么
P(T)=P(∑zk)=∑P(zk)
(2)
1.6 电站生命力的计算
为求每一级实现的概率,结合图论生命力的定义和建立的概率模型,先假设所有可能出现的事件,根据(1)式即可求出其出现的概率;在图中,破损的节点及与之相连的连线就全部去掉,构成原图的子图,再根据图论生命力的定义,将所有的子图分类,根据(2)式即可求出各级的概率;对于加权值的求解,首先构造评判矩阵,运用特尔斐法进行两两比对打分,并检验各判断矩阵均是否满足满意一致,再求出各判断矩阵的特征向量并归一化,即得各单排序结果,结果为:
W=[0.4 0.3 0.2 0.1]
至此,电力生命力的评估可以完全依靠图论的知识和定理求解。借助计算机高速的计算性能,对于一般的图论模型,都能很快解决。
2 图论模型的解算
2.1 损伤概率估计
某舰在一次命中时,系统的各设备的损伤概率从节点1到12分别为:0、0.12、0.12、0.06、0.06、0.06、0.06、0.05、0.05、0.04、0.04、0.03,此数据是通过对某舰在战斗中受舰舰导弹攻击时,舰艇各部位受攻击的可能性的估计,得出来的概率。
2.2 路搜索及求解
应用图论知识以及数据结构的算法进行各级通路的搜索。首先将图转变为关联矩阵,然后对满足条件的子图进行穷举[3],之后计算各子图出现的概率,将计算出的概率进行迭加,即是要求的完好概率。其流程图见图2。
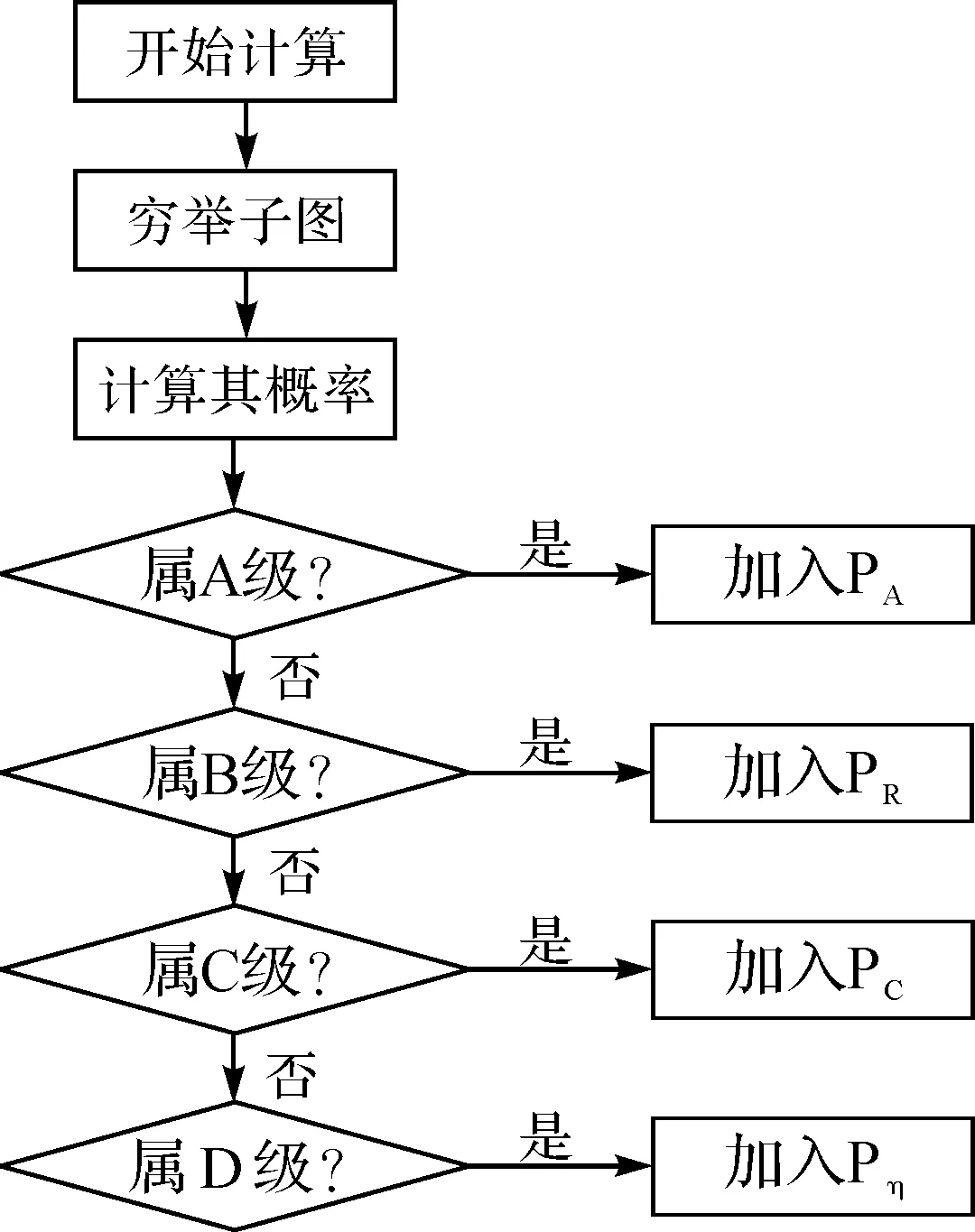
图2 程序流程
经编程计算,第A、B、C、D级的概率分别为0.941 4、0.910 9、0.663 4、0.528 4。
2.3 生命力指标
生命力指标I=P×W,其中P为各级概率所构成的行向量,而W为加权值所构成的列向量,即:
I=0.4×0.941 4+0.3×0.910 9+0.2×0.663 4+0.1×0.528 4=0.835 4
所以,此舰电力系统的生命力指标为0.835 4。
3 分析
为了更好地说明问题,分别用图论分析法和故障树分析法分别对两个电机、四个电机、六个电机及八个电机的同结构的电力系统,在同样的一次导弹命中下进行生命力评估,得出结果如图3所示。
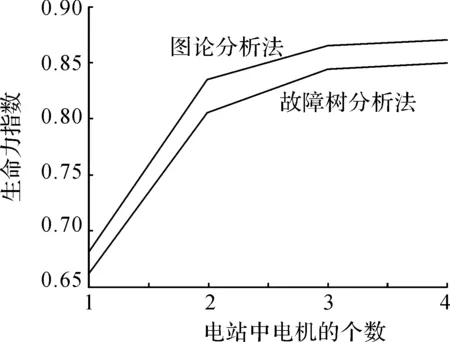
图3 生命力曲线
图中的横坐标为一个电站中电机的个数,总电机数为其两倍;竖坐标为其对应的生命力指数。由图中可以得出:电站只有一个电机,生命力指标确实太小,只有0.67到0.69。当设置两个电机时,生命力急剧增加,增至0.79到0.86。而在两个电机以上,生命力指标增加并不大,反而会增加舰艇的重量,增加舰艇的维修保养的费用,对中型舰艇,没有必要将系统弄得这么复杂。另一方面,图论分析法评估出来的生命力指标比故障树分析法的要高,见表1。
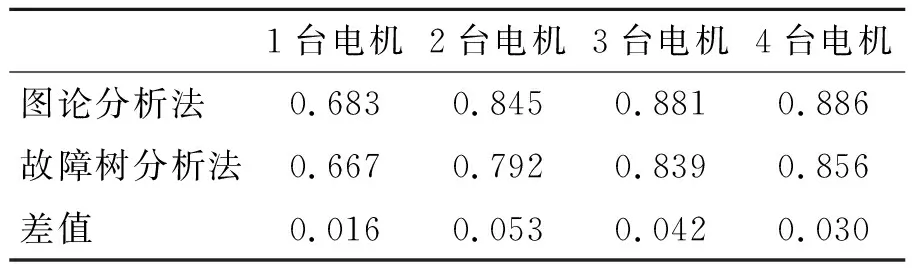
表1 结果比较显示
这是因为,用故障树分析法对系统评估时,省略了同层元素之间的关系,从而省略了电力系统中跨接线的作用,因而会使生命力指标下降。
4 结论
针对以往以故障树分析法对作战舰艇的生命力评估中误区,提出了图论分析法,为海军在作战舰艇的论证设计阶段提出明确合理的生命力要求提供了科学手段,并为舰艇的生命力优化设计提供了具有较好可操作性的考核方法。
[1] 浦金云.舰船生命力论证[D].武汉:海军工程学院.1991:141-160.
[2] 顾基发,李维铮等.运筹学[M].北京:清华大学出版社.2005:251-268.
[3] 严蔚敏 吴伟民.数据结构[M].北京:清华大学出版社.1997:156-183.
[4] 王树禾.图论及其算法[M].合肥:中国科学技术大学出版社.1990:1-44.
[5] 庄楚强,吴亚森.应用数理统计基础[M].广州:华南理工大学出版社.2004:1-22.
