一种处理高阶面元法中奇异积分的方法*

，2

1.上海交通大学 船舶海洋与建筑工程学院 上海 200030 2.上海交通大学 海洋工程国家重点实验室 上海 200030

自从Hess和Smith[1]用一阶面元法求解三维势流问题以来，面元法作为一种有效的数值方法已被广泛地应用于求解空气动力学和水动力学中的三维势流问题。最初的面元法中存在几个缺点，如物面用平面四边形面元离散，相邻面元间存在间隙；在离散大曲率的曲面时必须要有大量的面元，为此需要大量的计算时间；曲面上的源(汇)强度在面元边界上不连续。

为了克服低阶面元法的不足，人们引入线性或二次的函数表达面元，并在面元上分布一阶或二阶多项式源项。近年来，由于三次样条、B样条以及非均匀有理B样条(non-uniform rational B-splines, NURBS)在工业产品外形设计中的广泛应用，人们已经把他们应用到高阶面元法中以表达物面几何和速度势[2-5]。对于高阶面元法中的Rankine源项，Maniar和Danmeier以及Lee等[2-4]均运用三角形细分和级数展开的方式来近似求解。该方法在计算中较为复杂。赵成璧[5]的方法是离散第二类Fredholm积分方程，再直接高斯积分。该方法在场点离面元较远时可获得较好的结果，而当场点离面元较近时，数值积分的精度将受到很大的影响。

在处理基于B样条的高阶面元法中的奇异积分时，根据场点到面元的距离把曲面积分分为远场积分和近场积分。远场积分中，直接应用高斯-勒让德公式；近场积分中，采用Telles等[6-7]介绍的方法，先对积分函数进行三次多项式变换，然后应用高斯-勒让德公式。

1 数学公式

1.1 数学模型

考虑物体在无限静止流体中以匀速U向前运动，定义一个固定在物体上的右手直角坐标系o-xyz(图1)。假设流体是不可压缩理想流体，流动无旋，则存在定常扰动势φ满足下列边值问题：

(1)

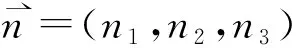
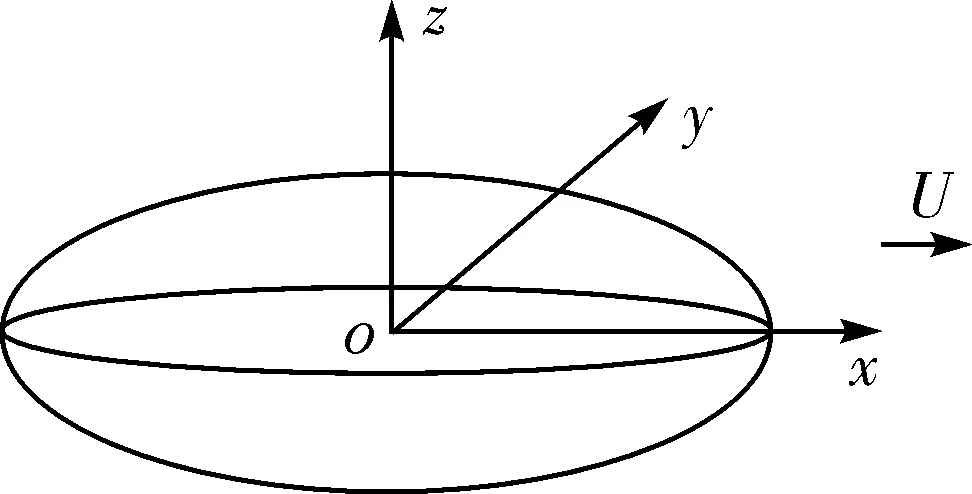
图1 坐标

(2)

式中：φ(q)——物面上源点q(ξ,η,ζ)处的源(汇)强度；

S——物面。

把式(2)代入式(1) 中得到确定源(汇)强度的第二类Fredholm积分方程。

(3)

1.2 有关物理量的表达

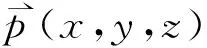
有

(4)

式中：u0、v0——代表NURBS曲面中的两个参数方向；

dij——物面控制点网格；

m、n——u0、v0方向上物面控制点的数目；

Ni、g(u0)、Nj、h(v0)——定义在u0、v0上的B样条基函数；

wij——权因子；

g、h——u0、v0上B样条基函数的阶数。

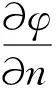
(5)

式中：u、v——B样条曲面中的两个参数方向；

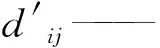
m′、n′——u、v方向上控制点的数目；

Ni,g(u)、Nj,h(v)——B样条基函数；

g、h——u,v上B样条基函数的阶数。

把式(4)、(5)代入式(3)中，可以得到用B样条参数表达的积分方程：

(6)

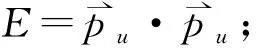
(7)

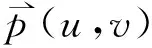
2 数值方法

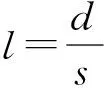
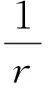
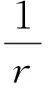
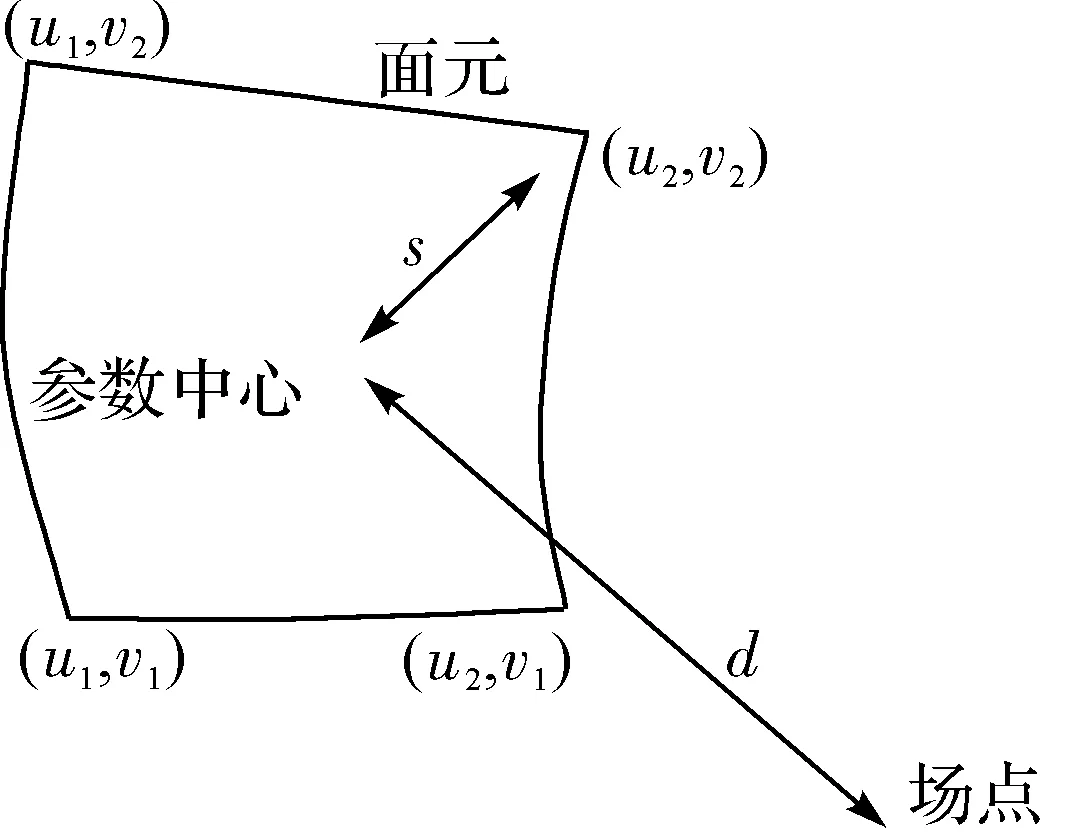
图2 场点与面元的关系

在结合高斯-勒让德公式积分时，三次多项式变换在不对面元进行任何细分的情况下，可以使高斯点自动向奇异点靠近，这个特性将有助于提高准奇异积分的精确性。因此，对于近场积分，先把式(6)中的积分函数进行三次多项式变换，然后再结合高斯-勒让德公式积分。

3 数值计算与结果比较

3.1 平面积分

为了验证三次多项式变换法的效果，考虑以下准奇异的二重积分

(8)

其中a,b为常数。在此使用8×8的高斯-勒让德公式，分别采用直接积分和经三次多项式变换后的积分。表1给出了计算结果和解析解的比较。

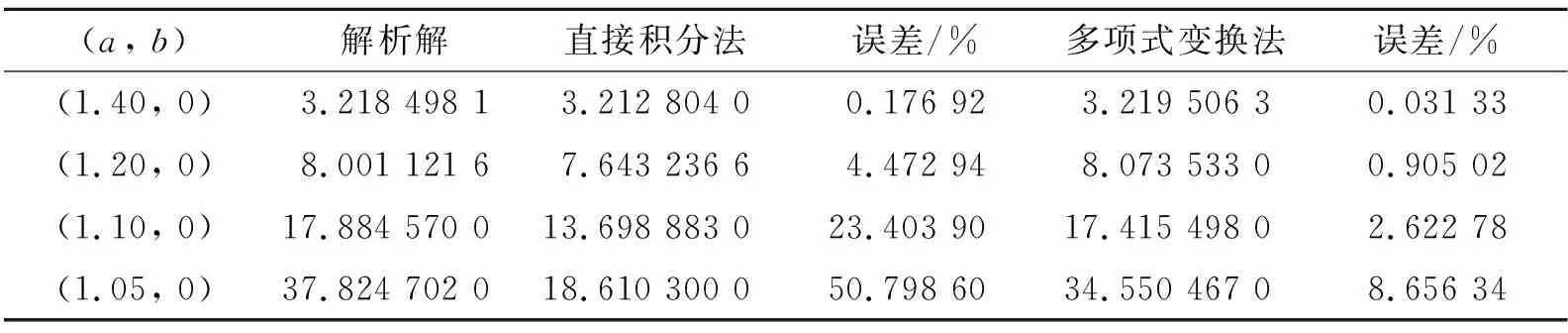
表1 两种奇异积分计算结果对比

从表中可以看出，当场点在(1.40，0)处时，由于它离面元相对较远，直接积分法和多项式变换法的计算误差都较小，但随着场点离面元距离的减少，当减少到(1.05, 0)处时直接积分法的误差迅速增大到50.80%，而多项式变换法的误差仅为8.66%，说明后者有着比前者更好的计算精度。

3.2 圆球

考虑一单位半径的球体以单位速度沿x轴正向运动，分别采用直接积分法和文中所介绍的方法对定常扰动势进行了计算。

表2给出了计算结果。从表2中可以看出，两种方法的计算结果均和解析解比较吻合，但本文方法的计算误差更小，尤其在靠近x=-1.0处。其中一个重要原因是在球的NURBS表达中，靠近x轴两端的面元较小，场点离面元相对较近，积分的奇异性表现得非常明显，直接积分将忽略这种特性，导致计算误差，而本文的计算方法通过对积分函数进行三次多项式变换，提高了计算精度。

表2 球面速度计算结果的对比

3.3 椭球

采用文中介绍的方法，对一系列以单位速度平移的椭球体在第二模态下的附加质量系数K22=3λ22(4πρabc)进行了计算，其中λ22是附加质量，ρ是流体密度，a、b和c分别是椭球体的三个半轴长；在此a∶b∶c的值分别取7∶1∶1, 5∶1∶1, 3∶1∶1, 2∶1∶1和1∶1∶1。根据三半轴的比值，布置不同的面元数。计算结果与Lamb给出的解析解和文献[7]中的计算结果(直接高斯积分法)进行了比较，如图3所示。可以看出，本文的结果比文献[7]的计算值更接近于解析解。

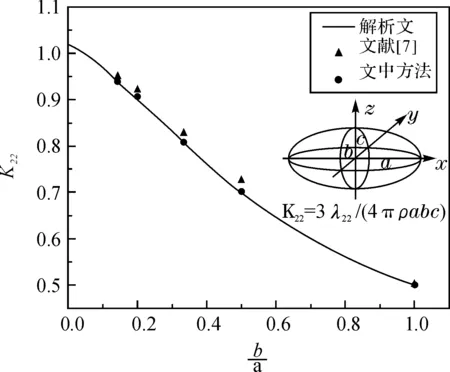
图3 椭球体附加质量系数 K22

4 结束语

本方法为解决高阶面元法中的奇异积分问题提供了一种有效的手段，在船舶运动性能预报相关的m项计算和水动力系数计算中具有较大的应用价值。

[1] Hess J L， Smith A M. Calculation of nonlifting potential flow about arbitrary three-dimensional smooth bodies[J]. Journal of Ship Research, 1964(7):22-44.

[2] Maniar H D. A three dimensional higher order panel method based on B-splines[D], MIT, Massachusetts, 1995.

[3] Danmeier D G. A Higher-Order Panel Method for Larger-Amplitude Simulation of Bodies in Waves[D]. MIT, Massachusetts, 1999.

[4] Lee C H，Newman J N, Solution of Radiation Problems with Exact Geometry, Proc. of 16th International Workshop on Water Wavers and Floating Bodies[C], Hiroshima, Japan, 2001：93-96.

[5] 赵成璧. 船舶曲面设计现代方法与软件系统的研究[D].武汉： 武汉交通科技大学, 1999.

[6] Telles J C F，Oliveira R F. Third degree polynomial transformation for boundary element integrals: Further improvement[J]. Engineering Analysis with Boundary Elements, 1994(13)：135-141.

[7] 王化明. 基于NURBS高阶面元法的有航速船舶辐射问题数值计算研究[D].武汉：武汉理工大学, 2005.