数学教学中的知识、方法与思想

陈立群

数学教学中的问题症结

在日常的数学教学中，有些教师将教学仅仅停留在知识点的罗列上，缺乏方法的指导，因而使教学囿于识记的层面。教师靠机械重复来加深学生的印象，学生则靠死记硬背学数学，结果学得既苦又累，成绩也差。

比如，在立体几何的复习课上，由于老师没有很好地用“证明两直线异面垂直”的方法把相关知识串联起来，而只是把“两直线的异面垂直是通过平行移动后两相交直线成90°”的定义作为知识点重新告诉给学生，所以当学生面对像下面这样的问题时就束手无策了。

例1.如图，V-ABC是一锥体木块，P为面VBC上一点，现要通过P点在面VBC上画C一条直线l，使l⊥VA，请写出画法。

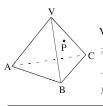
还有一些老师经过较长时间的教学实践积累了一些解决问题的方法，善于把知识通过方法串联起来，能够一题多解，这常使学生羡慕不已，惊叹老师解题的功夫了得。遗憾的是，这些教师的眼睛盯在应试上，教学只限于方法技能的层面，却往往为教方法而教方法。

请看这样的教学：

例2.已知x2-4xy+5y2+2x-6y+2=0，求x、y的值。

教师一口气给出了三种解法：

解法二：由x2-4xy+5y2+2x-6y+2=0，把它看成关于x的方程x2-（4y-2）x+5y2-6y+2=0，令△=（4y-2）2-4（5y2-6y+2）=0，即y2-2y+1=0，∴y=1，代入得x=1。

解法三：观察原式系数1-4+5+2-6+2=0成立，可知x=y=1是原方程的解。

这里，为什么要配方，为什么可以令△=0等等，学生全然不知，只能机械地记住它，以备后用。

在课堂上，老师往往形式上说变就变了，辅助线想添就添了，究竟基于什么方法和思想，学生不甚明了。靠“题海战术”，老师讲上百个，学生练上千遍，学生的数学能力仍然没有真正增强。

一般来说，人的能力可分为本能、技能、智能三种。大量的、机械的、重复的解题方法技能训练，固然有一定的应试功效，但其负面的作用是使技能退化为“本能”。因为这样训练出来的学生，在考试时首先考虑的是老师有否讲到过，一旦讲过，接下来的就是一个本能的过程。而我们的教学目标理应是由技能上升到智能。从而达到举一反三、融会贯通。缺乏数学思想的升华，正是当前数学教学中问题症结所在。

領悟教学思想和方法是数学教学的要务

新课程强调以教学方式的转变促进学习方式的转变。教学中不仅要教给学生数学知识，而且要揭示获取知识的思维过程，把知识与思想的种子播种在学生的心田，促进学生对数学思想方法的领悟。

数学方法与数学思想互为表里，密切相关，前者呈“显性”，后者为“隐性”，两者都以一定的知识为基础，反过来又促进知识的深化以及向能力的转化。方法是实施思想的技术手段;思想则是对应方法的精神实质和理论根据。数学教学内容是数学基础知识、数学方法和数学思想的有机结合，在基本方法和思想的指导下驾驭数学知识，就能培养学生的数学智能。在数学课上，学生往往只注意了对数学知识的学习，而忽视了联结这些知识的思想观点及由此产生的解决问题的方法与策略。而数学思想方法揭示了概念、原理、规律的本质，是沟通基础知识与能力的桥梁。正如数学家乔治·波利亚所说：“完善的思想方法犹如北极星，许多人通过它而找到正确的道路。”只有搞清楚为什么要选用这个方法，上升到数学思想的层面，遇到质同形异问题才不会无从下手，遇到新情景下的新问题，才有可能创造性地解决。

笔者看到在一节高三复习课上，老师讲解一些有关不等式的练习，其中有以下几题：

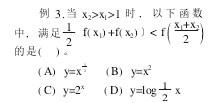
一些学生在运用分析法的基础上：

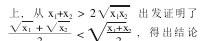
老师听说不少学生选对了，只顺便提了一句，还可以用数形结合的方法，并在黑板上画了右图，既未作“向上弯”和“向下弯”的凹凸性的“本质揭示”，也未作从两个到n个的数值比较的原理推广。本题中所含的真正鲜活的数学思想被一带而过，遗憾之至。

教师的讲解就事论事，流于形式和表面，不作源头上的本质揭示，学生自然不可能到达举一反三、触类旁通的境界。在同一个练习里，还有以下两例：

后再求证。没有一个学生想到它们与例3是形异质同的问题。

掌握数学思想是教学学习的最高境界

数学思想是在数学活动中解决问题的基本观点和根本想法，是对数学概念、命题、规律、方法和技巧的本质认识，是数学中的智慧和灵魂。而在数学课堂上，往往看不见教师对数学思想作生动活泼的阐释，却总是循著概念、例题、练习、作业的模式，把一大堆形式化的定义、定理、法则、公式呈现给学生，单调枯燥，学生学得被动，课堂气氛沉闷。有时学生尽管并不理解这些概念和符号，但不得不死记硬背、机械套用，以对付考试。老师还常常抱怨学生不记课堂笔记，其实，课堂上听不懂而记下来，只会陷入恶性循环。

胡炯涛先生认为：“数学教学不能满足于单纯的知识灌输，而是要使学生掌握数学最本质的东西，用数学的解法，循此培养和发展学生的数学能力。”只有搞清楚为什么要选用这个方法，揭示本质，才能培养学生的数学思想，提高学生的数学素养，才能真正培养学生的创新精神和创新能力。大千世界中所遇到的问题是原生态的，远不像书上的题目那样经过高度抽象和概括，需要我们用数学的观点和思想去发现、概括，乃至创造。

在当前的“中考”、“高考”制度之下，学校教学无法回避“应试”的要求，不能不考虑学生和家长的现实需要。但作为一名数学教师，更应着眼的是：学生走出校门若干年后，当具体的数学知识内容乃至方法都遗忘的时候，而对于数学问题所特有的思考、分析、解决方法——数学观念、数学思想能否长存。

这些“观念”与“思想”可以提供他在解决工作、生活中的问题时的宏观的理念指导，可以使他很快恢复对数学问题本身的理解、把握与解决。举个浅显的例子：加拿大多伦多的城市街道两旁的楼房编号，是以一条东西向的Bloor街与一条南北向的Young街的交叉口为原点，即零号，再向四个方向依次编号，即Bloor街东1，3，5，…2，4，6，…Young街南1，3，5，…2，4，6，…其他街道与这两条街大致平行也如此相应编号。即使外国人，只要看一下编号，就知道离市中心有多远;城市往各个方向扩展，都不会出现街道编号上的混乱变更等问题。这应该说，最初的规划设计者较好地活用了直角坐标系这一数学原理。我们在数学教学中，应当注重这种数学智慧的培养。

总之，知识是基础，方法是中介、手段，思想才是本原。有了思想，知识与方法才能上升为智慧。数学教学应该教给学生智慧，为学生的创新能力打好基础。世界著名高等学府哈佛大学门前有句话：“为增长智慧走进来，为服务祖国和同胞走出去。”为增长学生的智慧而教，这应是教师从事教学工作的核心价值。