数学中的简化

欧阳维诚

晚唐诗人杜荀鹤的“桑柘废来犹纳税，田园荒尽尚征苗”，高度集中地揭露了封建统治者对农民的巧取豪夺、敲骨吸髓的行为.诗人这种精选典型材料、省略次要情节、把深刻的社会矛盾集中在一联中凸现出来的写作风格，对我们学习数学很有启发.

在解数学题时，有时题目的条件分散复杂，为了抓住要领，应该学习杜荀鹤写诗的办法，尽量简化那些不必要的条件，高度浓缩那些次要条件，把题目的条件高度集中，让它在一个较小的范围凸现出来.这样，我们就容易抓住主要矛盾，迅速找到题解的途径.

这类问题，在各种级别的数学竞赛中最容易碰到.

安徽省高中数学竞赛就有这样一道试题：

一条长为ｎ的线段分成ｎ段，两个端点分别染上了红色或蓝色，其余的分点任意染成红色或蓝色.如果一条线段的两个端点的颜色不同就叫作标准线段，否则称为非标准线段.证明：不管你怎样给分点着色，只要两个端点的颜色不同，标准线段就一定有奇数条.

这个问题的条件是复杂的，线段的长度是一个可变的整数，ｎ个分点（除了两个端点外）的着色又是任意的．如果不把条件高度地集中在较小的范围内凸现出来，就很难抓住问题的实质.

如图１，假定ＡＢ是一条长度为ｎ的线段，端点Ａ被染成了蓝色，端点Ｂ被染成了红色，其余中间的点Ｃ、Ｄ、Ｅ、Ｆ、Ｇ、Ｈ、Ｉ、Ｊ、Ｋ、Ｌ等被任意染成了红色或蓝色.

问题的焦点是要求出标准线段是奇数条还是偶数条.因为标准线段只与它的两个端点的颜色有关，与它的长短无关．因此，只要两个端点不同色的线段就是标准线段.现在我们设想在给各分点染色的时候是从左至右逐个染色的，首先给Ａ染上了蓝色，要想得到一条标准线段，一定要换一种颜色才能做到.因此，换了几次颜色就得到几条标准线段.当我们把那些与前一个点颜色相同的点去掉之后，并不影响标准线段的条数.这时，图１就变成了图２（打“×”的地方表示去掉的点）．

要求出标准线段的条数，只要数一数图２中改变颜色的次数，由于图２中的点仍然是任意的，还有必要加以浓缩：

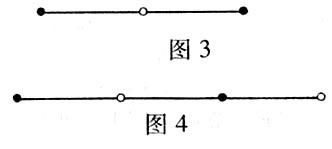
从图３、图４中可以看出，任何两点之间，不管它们中间有多少点，也不管这些点的颜色改变了多少次，但是有一点是很清楚的：如果两点之间改变了偶数次颜色，换句话说，两点之间包含了偶数条标准线段的话，这两点一定是同色的；反之，如果两点之间改变了奇数次颜色，即两点之间包含奇数条标准线段，则这两点一定是异色的.因此，我们在图５中，从左边的Ａ点开始，把任何一个与Ａ同色的点（例如Ｅ）之间的一段切掉之后，一定切去了偶数条标准线段.如果原来有奇数条标准线段，剩下的一节也仍然有奇数条标准线段，反过来也一样.

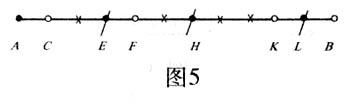
如图５，当我们切去ＡＢ上的ＡＥ一节后，因Ａ、Ｅ两点是同色的，所以，原来ＡＢ上标准线段的条数与剩下一节ＥＢ上标准线段的条数，奇偶性是相同的.类似的，我们可以逐渐地切去ＥＨ、ＨＬ等，剩下的一节都与原来的ＡＢ上标准线段的条数有相同的奇偶性．最后既然只剩下一条标准线段ＬＢ，１是一个奇数，所以，原来ＡＢ上的标准线段的条数也一定是奇数.

其实，在图５中，因为Ａ点与Ｌ点同色，一开始我们就可以一次把ＡＬ切掉，只剩下一条标准线段ＬＢ，就推出了我们所要的结论.

我们再看广东省的一道数学竞赛题：

证明：在任意５个正整数中，一定可以找到３个数，使它们的和是３的倍数.

这个问题的困难之处在于所给的５个正整数是任意的，它们可大可小，可异可同，讨论起来很不方便.我们可以先抓住一个要点：

将３个正整数中的任何几个去掉３的若干倍数之后，并不影响剩下的３个数之和是不是３的倍数.

例如，我们用圆点的个数来表示３个正整数，它们用３除的余数用方框内的圆点表示.

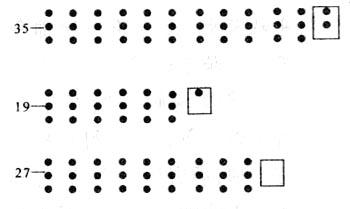
现在将３个数中的几个去掉一些３的倍数，剩下的３个数是：

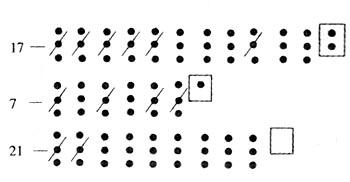
原来的三个数之和３５＋１９＋２７＝８１，是３的倍数；新得到的三数之和１７＋７＋２１＝４５，仍然是３的倍数.

根据这个道理，当我们把三个数中所有３的倍数都去掉之后，剩下的余数就只有０，１，２三种，这个问题就可以转化为一个更为简单的问题：

有５个数，它们分别是０，１，２三个数中的某一个．证明：一定可以从它们中找到３个数，使其和为３的倍数.

现在的证明就很容易了：５个数中或者０，１，２三者都有，那么０＋１＋２＝３，就是３的倍数.或者最多只有两种数，那么一定有一种数不少于３个，这３个数的和就是３的倍数.