基于浣熊算法优化的DV-Hop定位算法

摘 要：针对无线传感器网络定位算法中DV-Hop（Distance Vector-Hop）算法定位精度误差大与定位稳定性差的问题，提出了一种基于浣熊算法（Coati Optimization Algorithm， COA）的DV-Hop优化定位方法。首先，该方法利用多通信半径来精准计算节点间的跳数，同时运用加权跳距的策略，对未知节点的平均跳距进行精确修正，然后，用浣熊优化算法替代传统的三边测量法进行坐标位置估计，最终得到节点定位坐标。为了验证所提出的方法的有效性，文章对提出的改进算法进行了实验验证。结果表明，在同等条件下，在不同锚节点数量、不同通信半径和不同节点总数场景下，改进算法比传统DV-Hop算法的平均定位误差分别降低了61.64%、47.24%与65.11%，从而证明提出的改进算法具有良好的定位精度和较好的稳定性。

关键词：DV-Hop算法；浣熊算法；多通信半径；加权跳距；节点定位

中图分类号：TP18 文献标识码：A 文章编号：2096-4706（2025）02-0016-09

Optimized DV-Hop Positioning Algorithm Based on Coati Optimization Algorithm

ZHANG Xiao， JIANG Jinjing， LI Xin， PENG Tong

（School of Information Engineering， Zhejiang Ocean University， Zhoushan 316022， China）

Abstract： In view of the problems of large positioning accuracy error and poor positioning stability in the DV-Hop （Distance Vector-Hop） algorithm of wireless sensor network positioning algorithms， a DV-Hop optimized positioning method based on the Coati Optimization Algorithm （COA） is put forward. Firstly， this method makes use of multi-communication radius to accurately calculate the number of hops between nodes. At the same time， by applying the strategy of weighted hop distance， it precisely corrects the average hop distance of unknown nodes. Subsequently， the Coati Optimization Algorithm is adopted to replace the traditional trilateral measurement method for estimating coordinate positions， and finally the node positioning coordinates are obtained. To verify the effectiveness of the proposed method， the improved algorithm proposed in this paper is experimentally verified. The result demonstrates that under the same conditions， in scenarios with different numbers of anchor nodes， different communication radii and different total numbers of nodes， the average positioning error of the improved algorithm is respectively reduced by 61.64%， 47.24% and 65.11% compared with the traditional DV-Hop algorithm， thus proving that the proposed improved algorithm has good positioning accuracy and relatively good stability.

Keywords： DV-Hop algorithm; Coati Optimization Algorithm; multi-communication radius; weighted hop distance; node positioning

DOI：10.19850/j.cnki.2096-4706.2025.02.004

收稿日期：2024-07-13

基金项目：国家自然科学基金重点专项资助项目（62341127）

0 引 言

无线传感器网络（Wireless Sensor Networks， WSN）[1]在现代科技领域中的作用逐渐加强，成为不可或缺的一部分。WSN在一定区域内布设了大量传感器节点，各节点利用通信技术感知信息、处理数据，构成一个多跳自组织网络[2]。这些网络由一系列体积小、能耗低的传感器节点构成，各节点在特定的地理区域内进行分散部署。这些传感器节点能够利用先进的通信与感知技术，精确捕获并实时传递环境数据，包括温度、湿度、光照以及压力等关键信息。在数据采集、网络拓扑构建、事件检测、能量管理和多传感器协同等多个方面，无线传感器网络节点定位的准确性至关重要。

在无线传感器网络节点定位技术的实际应用中，DV-Hop算法展现出了其非测距定位算法的优势。该算法利用跳数信息来估算节点间的实际距离，随后结合三边测量法或极大似然估计法来精确求解节点的位置，在无线传感器网络定位技术中得到了广泛应用。虽然DV-Hop算法不需要额外的硬件设备，适用于节点密度较高的网络，但由于距离估计和位置计算中的误差累积问题，其定位精度往往受到较大影响。

为了提高DV-Hop算法的定位精度，许多研究者提出了不同的优化方案。张晶等[3]采用二通信半径，并使用加权误差最小化的思想对未知节点进行定位。董玉等[4]采用均方误差求解平均跳距，并引入蝙蝠算法进行节点位置估计。Zhang等[5]定义了一个偏差系数来修正节点之间的跳数值。Wang等[6]改变了跳数越大权重值越低的权重优化模型，构建了误差与跳数之间的关系模型。Chen等[7]提出了一种基于加权最小均方误差准则的锚平均跳距计算方法。吴雪敏等[8]提出了一种跳数分类的DV-Hop算法，用弹簧系数对应不同的跳数分类，提高节点定位精度。唐德红等人[9]设计了一种基于斯蒂芬森迭代的改进DV-Hop定位方法。随着优化算法的兴起，许多学者采用群体智能优化算法来减少目标节点的定位误差。刘登峰等[10]将定位问题转化为群体优化问题，利用布谷鸟算法和差分进化算法进行双种群并行搜索，有效提高了定位精度。余成成等[11]提出了一种DV-Hop定位算法的改进方案，该方案结合了多通信半径的策略，并通过优化遗传算法来增强定位精度。潘志远等[12]针对节点间跳数进行优化，采用双通信半径策略，并通过引入权重因子来完善适应度函数，利用蜣螂算法进行坐标计算。在针对不规则节点网络中的定位精确度提升问题，吴建锋等[13]引入了改进的粒子群算法来计算未知节点的位置。

针对锚节点之间的相互影响问题，现有的研究已经取得了一定的成果。然而，不同的权值分配策略所得的结果却存在较大的差异，并且未知节点的平均跳距结果极其依赖于锚节点平均跳距的精度，不可避免会造成误差的积累。利用元启发式算法、群体智能算法等应用于坐标计算需要考虑算法复杂度，算法的全局搜索能力以及局部搜索能力。根据以上研究，本文提出一种新的定位算法，即基于浣熊优化算法的DV-Hop定位算法（COMRW-D），以此来进一步提高定位精度。相比其他群体智能算法，浣熊算法在平衡全局搜索的探索和局部搜索的利用中具有明显的优势，收敛精度高。本文提出的优化方案主要从跳数修正、跳距修正和位置的求解三个方面进行优化：

1）最小跳数修正。利用多通信半径对传感器网络中节点之间的最小跳数进行修正，使节点间跳数估计更加接近实际情况，减小定位误差。

2）平均跳距修正。引入权重因子，计算加权跳距，使节点的平均跳距更加精确。

3）未知节点的位置求解。用浣熊优化算法代替传统的三边测量法，设置适应度函数，将定位问题转化为优化问题，对跳数和跳距优化后的结果进行不断迭代和搜索，找到更接近实际位置的最优解，得到更精确的定位结果。

1 相关理论

1.1 DV-Hop算法原理

DV-Hop算法是一种高效且通用的距离向量跳数算法，初次问世于2003年，由NICULESCU等提出[14]被广泛应用于各种无线网络中，例如无线传感器网络、无线局域网等。算法包括以下三个过程：

第一阶段计算从每个未知节点到所有锚节点的最小跳数。每个锚节点将数据包广播到网络。数据包包含以下信息：锚节点ID、坐标和初始化为0的跳数。当相邻节点收到数据包后，仅保存来自同一锚节点的最小跳数值，并将跳数值加1后继续传递给相邻节点。通过泛洪广播，WSN中的各个节点都能够得到到达所有锚节点的最小跳数。

第二阶段计算未知节点到锚节点的距离。经过第一阶段，每个节点都知道所有其他锚节点的坐标以及它到这些节点的跳数，因此每个锚节点都可以计算它到所有其他锚节点的平均跳距（Average Distance of each Hop， ADH）的值，公式如下：

（1）

其中，hij表示从锚节点i到j的最小跳数，（xi，yi）和（xj，yj）分别表示锚节点i和j的坐标。每个锚节点通过洪泛将其平均跳距广播到整个网络，未知节点会从多个锚节点接收数据包，并将距离其自身跳数最小的锚节点视为距离最近的锚节点。通过计算未知节点的平均跳距ADHu与锚节点的最小跳数hua的乘积估计未知节点到锚节点的距离dua，估计距离的计算如式（2）：

（2）

第三阶段未知节点坐标的计算，通过三边测量方法，就可以计算出来未知节点的坐标。

1.2 DV-Hop算法误差分析

尽管DV-Hop算法在实际应用中具有较高的定位覆盖率和较快的计算速度，但其不稳定的误差仍是需要解决的问题。误差主要来源于以下几个方面：

1）跳数误差。在DV-Hop算法中，未知节点通过记录锚节点的最小跳数来估算距离。在锚节点的通信范围内，不论相邻节点之间的实际距离如何，它们通常被统一视作1跳。然而，在实际部署场景中，节点的分布往往呈现出随机性，使节点间的距离呈现非均匀状态。因此，简单地将所有相邻节点都标记为1跳的处理方式，可能会在实际应用中引入一定的误差。此外，随着跳数值的增加，这种误差可能会逐渐累积。

2）平均跳距估计误差。DV-Hop算法通过计算网络平均跳距来估算未知节点与锚节点之间的距离。未知节点从距离自身最近的锚节点处获取平均跳距值，但现实情况下，节点往往不在一条直线上；并且可能会存在多个相同跳数的锚节点，只选择其中一个锚节点的信息而忽略了其他距离相同的锚节点的信息，对定位结果的影响很大。

3）定位算法选择误差。DV-Hop算法中，未知节点接收到锚节点广播的距离信息后，需要选择一种合适的定位算法进行位置估算，通常是利用三边测量法或最小二乘法进行的。三边测量法计算相对容易，三边定位算法仅仅依赖于距离的测量值，但是两个锚节点在同一条直线上无法求解；间距计算误差大时，最小二乘法可能会造成误差的累积，从而影响结果的准确性。

1.3 浣熊算法

浣熊算法（Coati Optimization Algorithm， COA）是由Mohammad等[15]于2023年基于对浣熊狩猎行为的模拟提出的，该算法具有进化能力强，收敛速度快，收敛精度高等特点。COA在平衡全局搜索的探索和局部搜索的利用中具有明显的优势，并且更具竞争力。

1.3.1 算法初始化过程

COA是一种元启发法，以长鼻浣熊为群体成员，每个浣熊在搜索空间中的位置决定了决策变量的值。在COA中，每个浣熊的位置代表候选解。在寻优空间里随机初始化种群：

（3）

其中Xi表示第i个浣熊在搜索空间中的位置，xi，j表示第j个决策变量的值，N表示长鼻浣熊的数量，m表示决策变量的数量，r表示区间[0，1]内的随机实数，uj和lj分别表示第j个决策变量的上、下限。

COA中长鼻浣熊的种群数量使用以下矩阵X进行数学表示，称为种群矩阵。

（4）

1.3.2 第一阶段：探索阶段

这个阶段是模拟浣熊群体进行捕猎的过程，该阶段使得COA在搜索空间中移动到不同的位置，说明COA在问题解决空间中的全局搜索能力。

在COA的设计中，种群中的最佳位置被假定为猎物的位置。此外，假设有一半的浣熊能爬上树，另一半在地上等待猎物掉下来。因此，浣熊在树上的位置可以用以下公式描述：

（5）

这里表示第i个浣熊计算的新位置，表示它的第j个维度，r表示区间[0，1]内的随机实数，M表示猎物在搜索空间中的位置，实际上指的是种群中最佳个体的位置，Mj是它的第j个维度，z表示一个整数，从集合{1，2}中随机选择，表示下取整函数。

猎物落地后，将其放置在搜索空间中的任意位置。基于这种随机位置，地面上的浣熊可以在搜索空间中移动，用下列公式来描述：

（6）

：（7）

其中，j=1，2，…，m，表示猎物在地面上的位置，是随机生成的，表示它的第j个维度，FMG表示其目标函数的值。

对于每个浣熊计算的新位置，如果它改善了目标函数的值，那么就会被接受，否则，浣熊将保持原先的位置，此过程用以下公式来表示，该过程可以被视为贪婪法则[16]：

（8）

其中表示第i个浣熊计算的新位置，表示它的第j个维度，表示其目标函数值。

1.3.3 第二阶段：开发阶段

在第二阶段即探索阶段的过程中，位置更新模拟的是浣熊在遇到捕食者和逃避捕食者的行为。浣熊在该策略中的移动使其处于接近其当前位置的安全位置，这代表着COA的局部开发能力。为了模拟这种行为，COA在每个长鼻浣熊个体附近生成一个随机位置：

（9）

：（10）

其中i=1，2，…，N，j=1，2，…，m表示COA第二阶段计算出的第i个浣熊的新位置，表示它的第j个维度，表示其目标函数值，r表示区间[0，1]内的随机实数，t表示迭代计数器，和分别表示第j个决策变量的局部下界和局部上限，lj和uj分别表示第个决策变量的下界和上限。

与开发阶段中类似，同样使用贪婪选择来决定是替换还是保留原先的位置：

（11）

其中表示根据COA第二阶段计算出的第i个浣熊的新位置，表示它的第j个维度，表示其目标函数值。

2 本文的定位算法

2.1 多通信半径

在DV-Hop算法中，修正最小跳数问题常用的方法为多通信半径[17]。设网络通信半径为R，将锚节点与邻居节点分为m级，网络中各锚节点与其邻居节点的实际距离为d，i ∈ [1，m]，跳数记为（Number of Hops， NoH）。m = 2，3的网络如图1所示。

NoH可写作：

（12）

经过改进之后，锚节点与邻居节点的跳数值不再是整数，是更加精确的小数，与距离更接近正比关系，有效地提高了数据的精确性，减小定位误差。本文将m的值取3，更好地适应节点之间的距离分布特点，提供更准确的位置估计，同时也避免了过高的计算和通信开销。

2.2 加权跳距

在原始DV-Hop定位算法中，设未知节点坐标为D（x，y），能与该未知节点通信的锚节点为A1（x1，y1），A2（x2，y2），…，An（xn，yn），根据DV-Hop原理的第一、二阶段可知，这些锚节点的平均每跳距离ADH为ADH1，ADH2，…，ADHn，到D（x，y）的跳数NoH为NoH1，HoH2，…，HoHn，那么D（x，y）到Ai（xi，yi）的距离di为：

（13）

未知节点会选择距离最近的锚节点的ADH作为未知节点自身的平均跳距，但是实际网络中节点在不同区域的分布状况是不同的，平均每跳距离也是不同的。因此，原始DV-Hop算法用单一的平均跳距不能正确反映网络状况，误差较大。

针对未知节点与不同锚节点之间的跳数，定义了加权系数，以修正各锚节点的平均跳距，从而消除单一锚节点与未知节点跳数所导致的不合理性。加权系数能够体现不同跳数的影响，即锚节点与未知节点间最小跳数较小（即距离较近）时，其对未知节点的影响较大，因此赋予较高的加权系数；反之，若节点与未知节点间最小跳数较大（距离较远），则影响较小，加权系数较低。通过加权系数来反映锚节点对未知节点的影响力，每个锚节点的平均跳距都根据其与未知节点的距离进行了相应的加权处理，锚节点加权系数wi的计算如下：

（14）

式中wi表示锚节点i的加权系数，n表示锚节点数量，NoHi表示锚节点和未知节点的最小跳数。

引入加权系数后，修正的未知节点的平均跳距公式如下：

（15）

其中ADHavgi表示未知节点i的加权平均跳距，ADHi是由式（1）得到的锚节点的平均跳距。

利用式（14）、式（15），我们可以得到修正后的未知节点的平均跳距，这一过程中，所有能与未知节点通信的锚节点的平均跳距都被纳入考量，锚节点和未知节点距离越远，加权系数越小。这样的处理方式，使得未知节点在计算自身坐标时，能够更准确地反映出网络的真实情况。经过优化后的未知节点u到锚节点a的距离dua可写为：

。 （16）

2.3 使用COA优化定位结果

本文选择使用COA算法来替代DV-Hop算法中的位置估计环节，适应度函数的设计使COA算法朝着最小化未知节点与锚节点距离差的方向优化，从而提升定位精度。

最小化适应度函数fitness可写作：

（17）

其中表示未知节点x到锚节点bi的欧式距离，di，j表示给定的未知节点j到锚节点i的距离，与d中给定的距离越接近，fitness值越小，我们可以利用迭代搜索使fitness最小，以达到精确定位未知节点x的目的。

2.4 算法流程

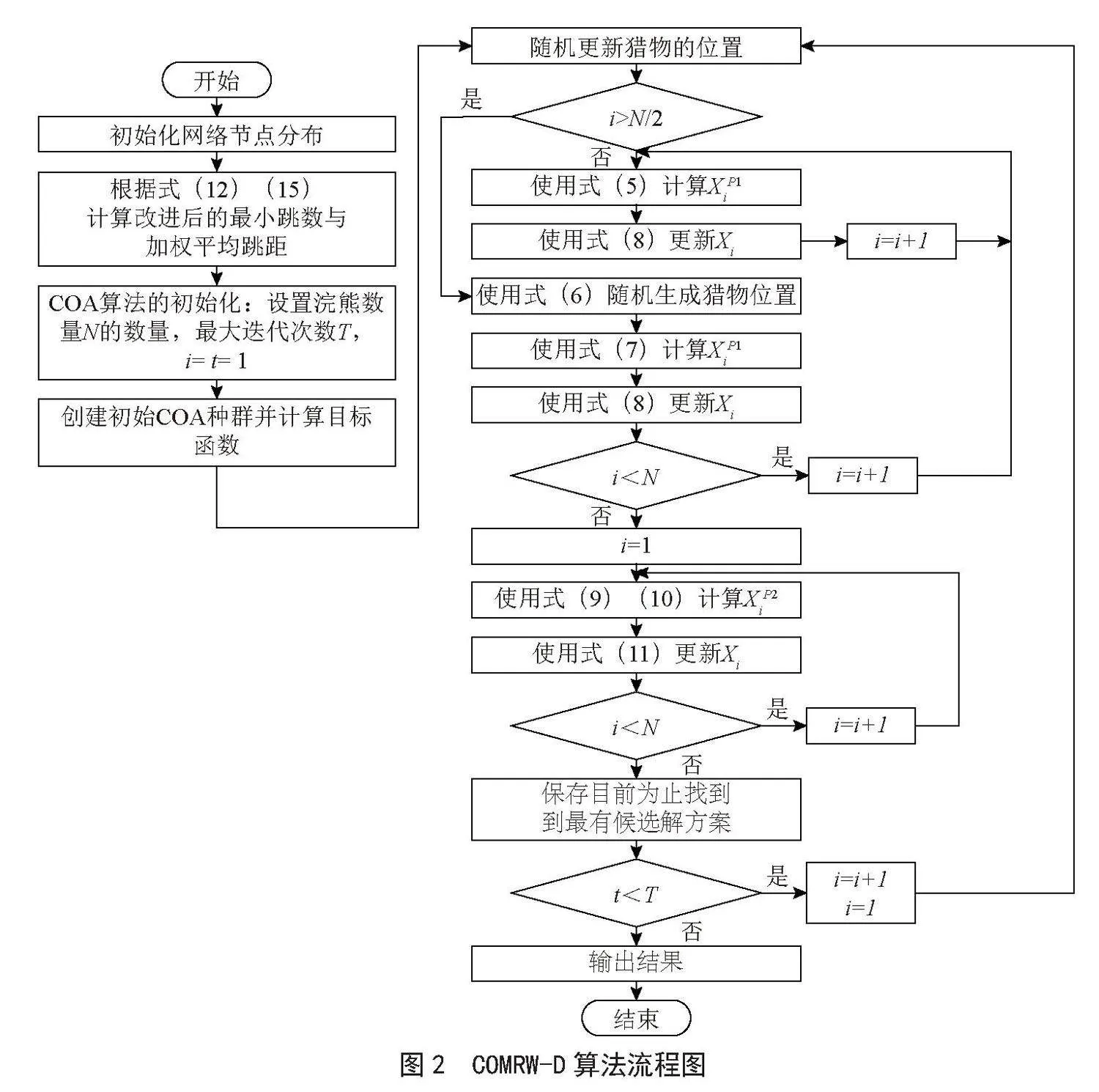
本文通过结合DV-Hop和COA两种算法，提出了一种基于COA的DV-Hop优化定位方法：通过引入多通信半径优化节点间跳数，使用加权跳距修正节点平均跳距，并利用浣熊优化算法代替传统的三边测量法进行坐标位置估计，命名为COMRW-D算法。

本文提出的COMRW-D算法流程归纳如下：初始化网络拓扑结构，包括节点数、锚节点数、通信范围等参数。生成随机坐标，并将节点分为锚节点和未知节点。在DV-Hop的第一个阶段用多通信半优化得到最小跳数数据后，每个节点利用式（15）得到修正后的加权平均跳距以提高定位精度。利用COA解决位置估计问题，设置COA的参数，将估计的未知节点位置作为初始位置，使用COA对其进行迭代优化，直至收敛。COMRW-D算法的流程如图2所示。

3 仿真结果与分析

在本节中，我们对提出的COMRW-D定位算法的性能进行评估，通过蒙特卡洛方法[18]来验证该算法的有效性，并将我们所提出的COMRW-D定位算法与相同网络条件下的DV-Hop、MRWDV-Hop[19]以及使用COA优化的COADV-Hop进行比较。

3.1 算法参数设置

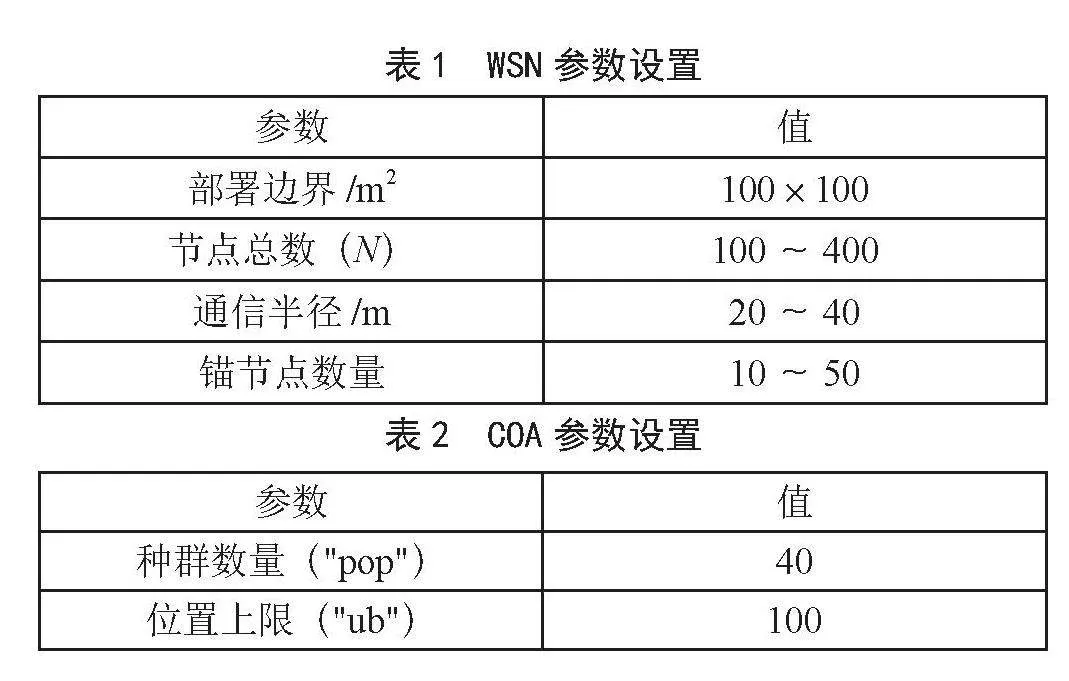
本文仿真实验在假设锚节点定位没有任何错误的情况下进行的，仿真实验参数设置如表1、表2所示。

3.2 评价指标

为了对算法的准确性与稳定性进行分析，本文引入两个评价指标，即归一化定位误差（ALE）[20]与定位误差方差（LEV）[21]。

ALE的计算可写作：

（18）

LEV则可以用下式计算：

（19）

式中绝对定位误差e与平均定位误差的计算如下：

（20）

（21）

其中N表示节点总数，R表示通信范围，（xi，yi）和（，）分别表示未知节点i的实际坐标和估计坐标。

实验中传感器节点在100 m×100 m的区域内随机分配，如图3所示。

3.3 改变锚节点数量对定位精度的影响

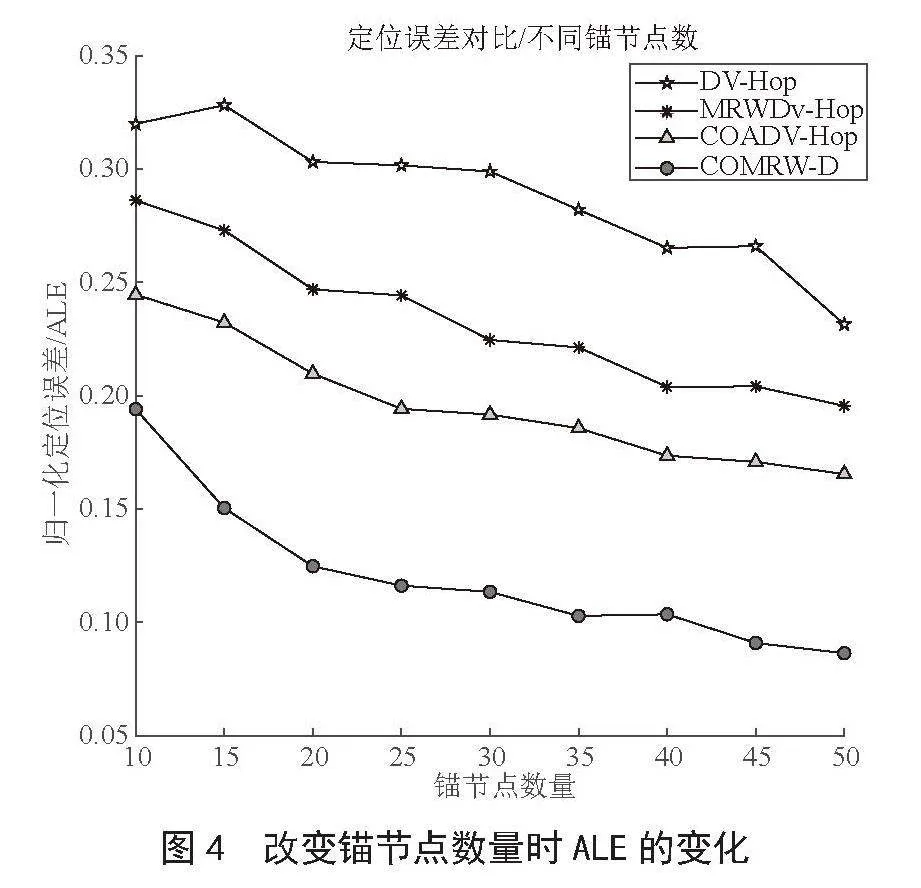
将传感器节点的总数设定为100个，每个节点的通信半径被设定为30米，将锚节点的数量从10个逐步增加至50个，进行5 000次实验，并对结果进行平均处理。

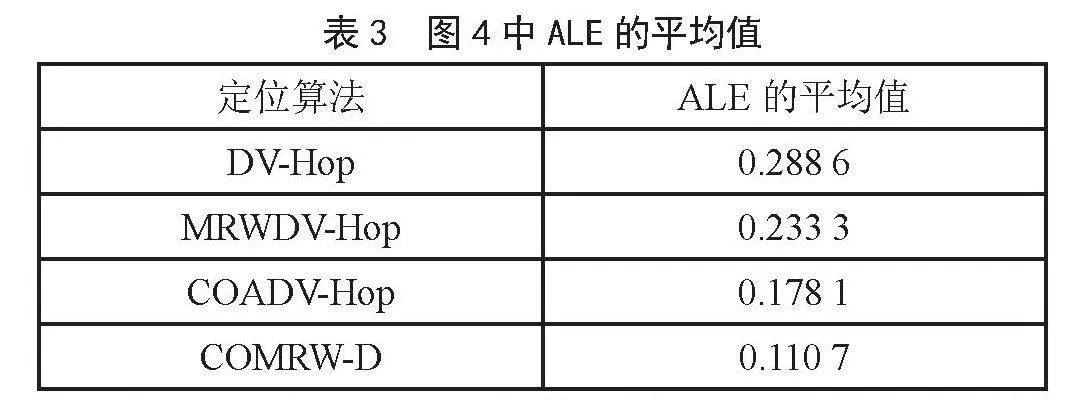
从图4中可以看出，四种定位算法的ALE值随着锚节点数量的增加而减小。其原因是随着未知节点一跳范围内锚节点数量的增加，节点间平均距离的误差减小，未知节点与锚节点之间的距离估计也变得更加精确。

表3展示了各种定位算法的ALE的平均值。经过对比分析，文中所提出的COMRW-D定位算法在ALE的平均值上相较于DV-Hop、MRWDV-Hop和COADV-Hop算法分别降低了61.64%、52.55%和37.84%。这一数据充分表明，COMRW-D定位算法的定位精度相较于其他三种算法更好。

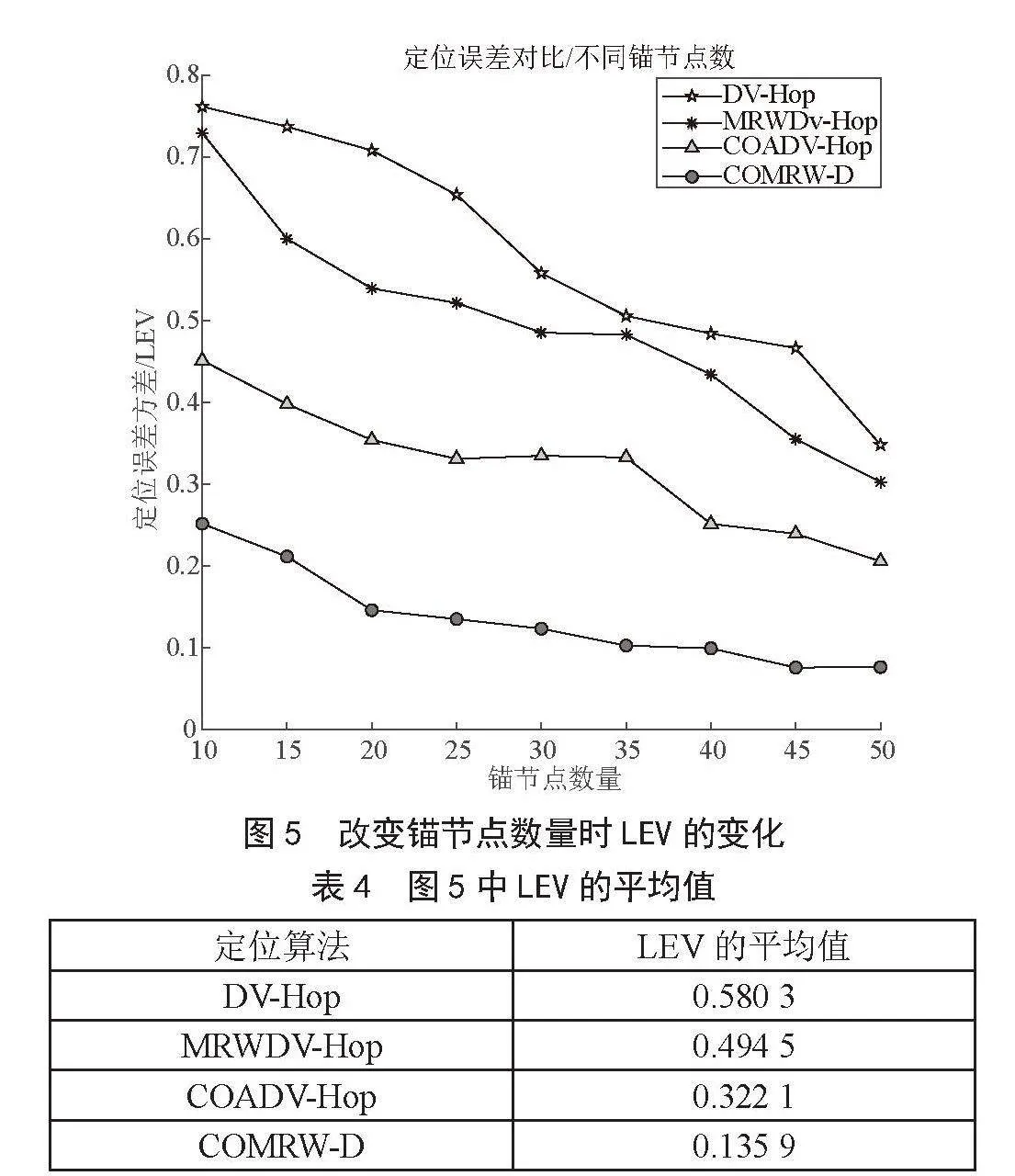
图5显示了四种定位算法的LEV随锚节点数量的变化情况。随着锚节点数量的增加，四种定位算法的LEV均逐渐降低。其原因是随着锚节点数量的增加，网络中的信息增多，定位算法可以利用更多的信息来提高定位的稳定性。

表4展示了锚节点数量增加时，LEV的平均值变化情况。通过对比分析，我们发现所提出的COMRW-D定位算法的LEV的平均值相较于DV-Hop、MRWDV-Hop和COADV-Hop算法，分别降低了76.58%、72.51%和57.81%。这一数据证明了从稳定性角度来看，COMRW-D定位算法在本次实验中的表现优于其他对比算法，有较高的稳定性。

3.4 改变通信半径对定位精度的影响

将传感器网络中的节点总数设定为100个，其中锚节点的数量为30个，逐步将通信半径从20米增加至40米，进行5 000次实验，并对结果进行平均处理。

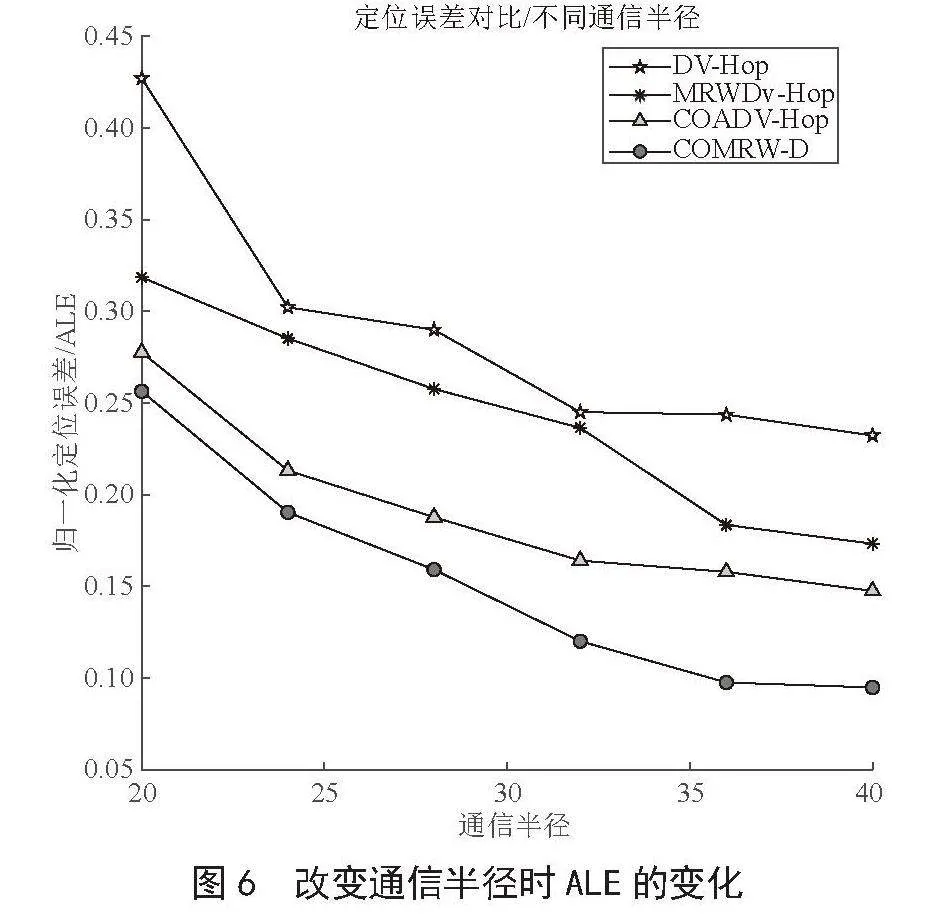
如图6所示，当通信半径逐渐增大时，各类定位算法的精度都有提高。这是由于当通信半径相对较小时，可用于与未知节点通信的锚节点数量相对较少，难以准确计算未知节点的位置；此外，还可能存在无法与其他节点通信的孤立节点，通过扩大通信范围，可以增加未知节点与锚节点的通信机会，从而提高定位精度。

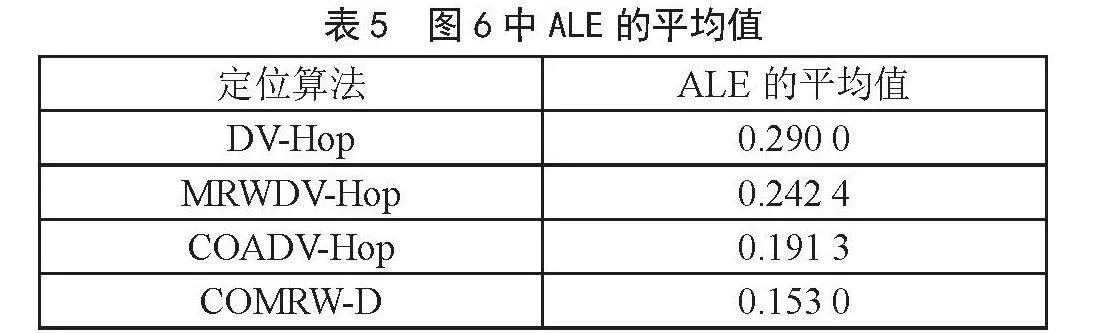
根据表5的数据，COMRW-D定位算法的ALE的平均值相较于DV-Hop、MRWDV-Hop和COADV-Hop算法分别降低了47.24%、36.88%和20.02%。这一结果表明，相较于上述三种定位算法，COMRW-D定位算法在定位精度方面更优。

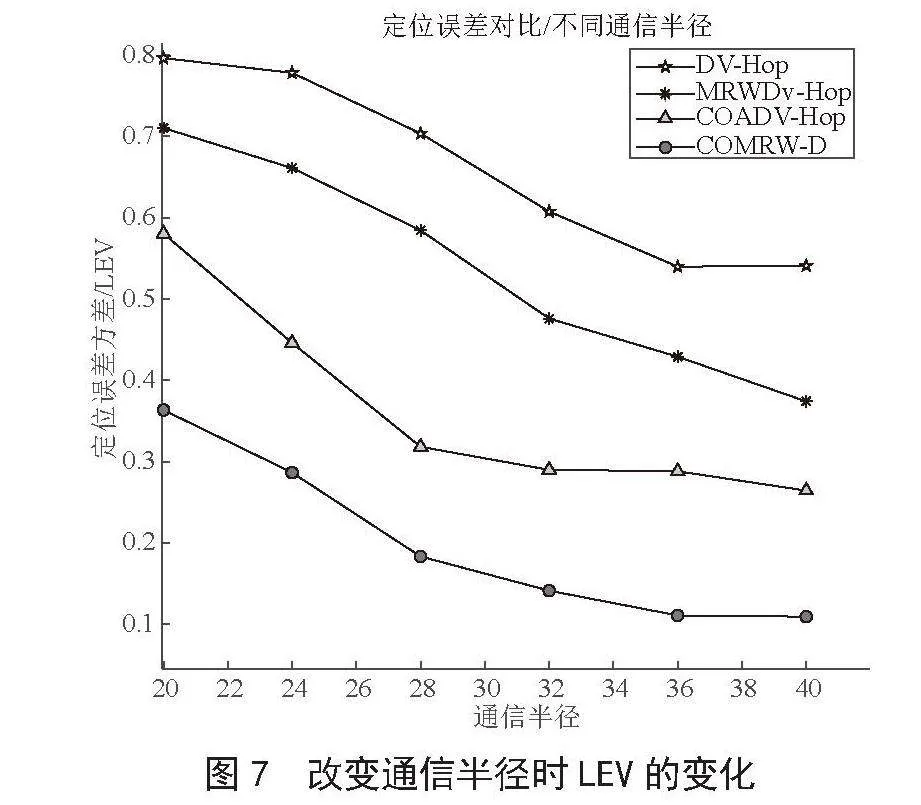
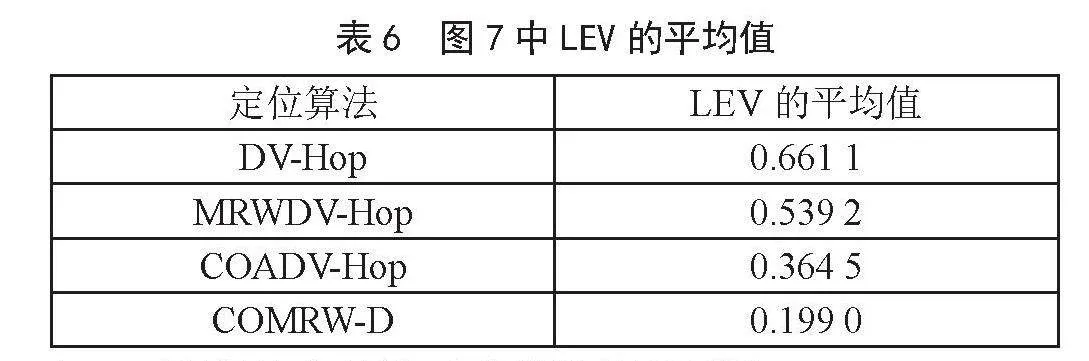
从图7可以看出，随着通信范围的增加，四种定位算法的LEV均下降，变得更加稳定。其原因是随着通信半径的增大，未知节点能够与更多的锚节点建立通信联系，从而获取更多的位置信息，使定位结果更加稳定可靠。

如表6所示，随着通信范围的逐渐增加，LEV呈现出下降的趋势。与DV-Hop、MRWDV-Hop和COADV-Hop这三种算法的LEV平均值相比，COMRW-D定位算法在通信范围变化的过程中，其LEV的平均值分别降低了69.90%、63.09%和45.40%。说明了在通信范围变动的情况下，COMRW-D定位算法相较于其他三种算法具有更稳定性的表现。

3.5 改变节点总数对定位精度的影响

将传感器网络中的节点总数设定锚节点的数量为节点总数的30%，通信半径为30米，节点总数从100个逐步增加至400个，进行5 000次实验，并对结果进行平均处理。

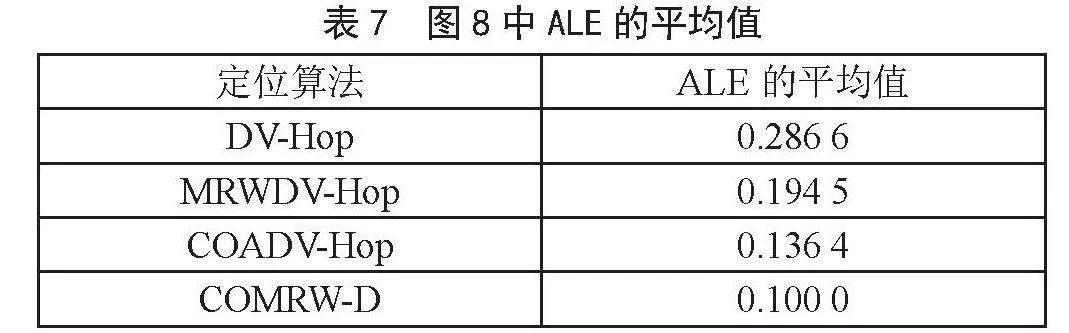
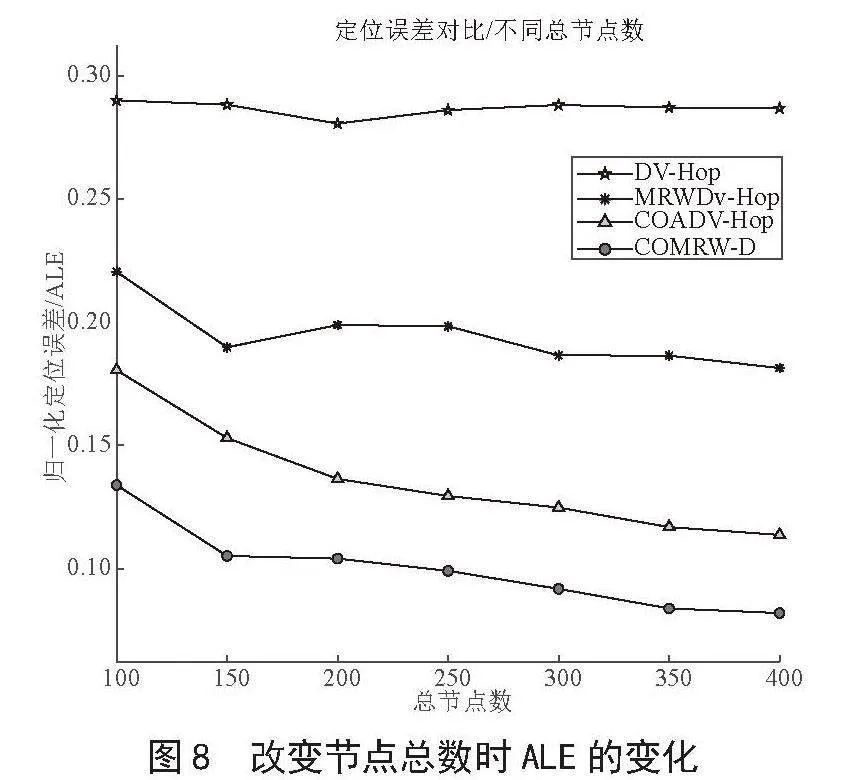
如图8所示，随着节点总数的增加，4种定位算法的误差均逐渐减小。其原因是随着节点总数的增加，网络连通性显著提高，未知节点可以接收到更多的辅助位置信息，从而提高定位精度。

如表7所示，与DV-Hop、MRWDV-Hop和COADV-Hop算法相比，COMRW-D定位算法的平均ALE分别降低了65.11%、48.59%和26.69%。因此，COMRW-D定位算法的定位精度高于上述三种定位算法。

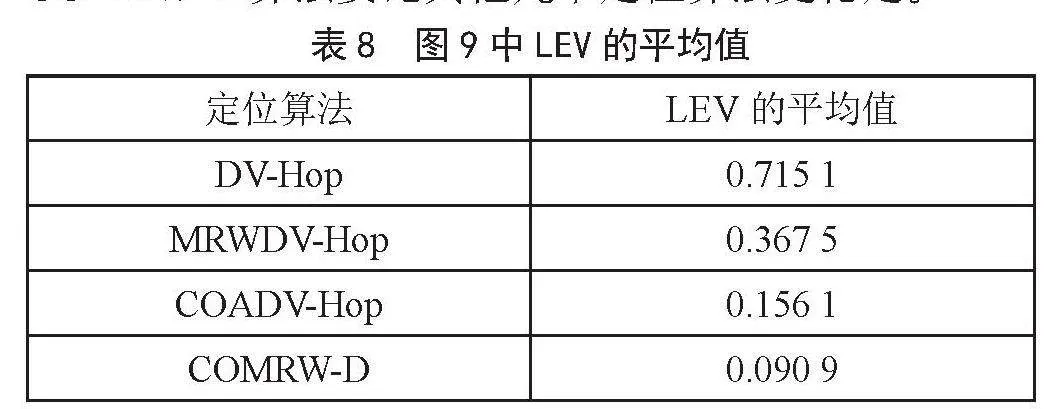
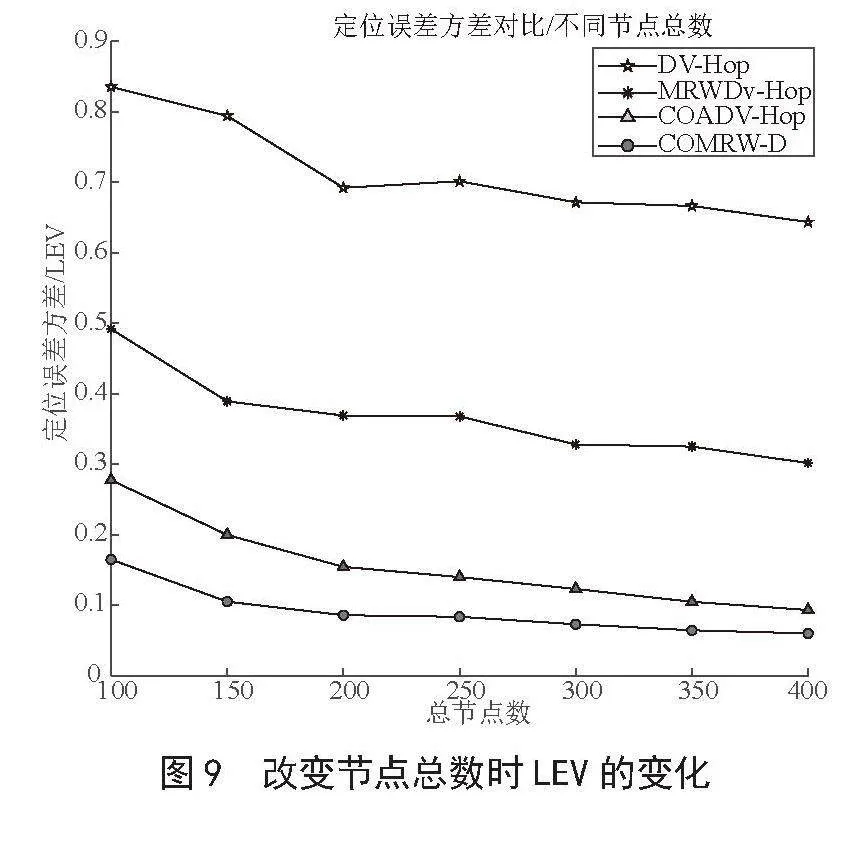
从图9可以看出随着节点总数的增加，四种定位算法的LEV值均逐渐降低，算法的稳定性逐渐增强。其原因为随着节点总数的增加，网络的连通性得到了提高，从而减少了由于个别节点异常或信息传输错误导致的定位误差，提升了定位的稳定性。

如表8所示，随着节点数的增加，定位误差方差逐渐减小，定位更加稳定，与DV-Hop、MRWDV-Hop和COADV-Hop算法LEV的平均值相比，COMRW-D定位算法的LEV分别降低了87.28%、75.26% 和 41.77%。在节点总数增加的情况下，COMRW-D算法要比其他几个定位算法更稳定。

4 结 论

针对传统DV-Hop定位方法存在的精度低、稳定性不足等核心问题，本文提出了一种创新的解决方案，即基于浣熊算法优化的DV-Hop定位方法。该算法结合了DV-Hop算法与浣熊算法，利用多通信半径和加权跳距来优化每个未知节点根据平均跳距计算自身坐标时的误差值；同时利用COA算法代替三边测量法来估计位置节点的位置，使定位结果更加精确且稳定。经过仿真实验验证，在调整锚节点数量、通信范围及传感器节点总数等多个变量时，本文所提算法相较于其他对比算法，如DV-Hop、COADV-Hop及MRWDV-Hop等，展现出了更为出色的精确性和稳定性。

在DV-Hop算法的改进过程中，其性能也在不断地被优化增强。本文基于DV-Hop算法，对最小跳数和平均跳距进行了修正，将需要迭代的浣熊算法融入其中增加了算法的复杂度。因此，如何在不牺牲算法性能的前提下，有效降低算法的复杂度是一个研究难点。在未来的工作中，我们将着重研究如何有效降低算法复杂度，提升其精度并降低能耗，关注如何将该优化方案应用到实际场景中，并进一步提高定位精度和鲁棒性。

参考文献：

[1] 余学帆.基于RSSI的无线传感器网络定位改进优化算法研究 [D].长春：长春工业大学，2021.

[2] ZHANG Q. An Improved Location Algorithm for Wireless Sensor Networks [J].International Journal of Performability Engineering，2018，14（11）：2674-2682.

[3] 张晶，李煜.改进的无约束优化3D-DV-Hop定位算法 [J].计算机工程与科学，2022，44（1）：75-83.

[4] 董玉，张治中，冯姣.基于测距修正和蝙蝠优化的改进DV-Hop定位算法 [J].电子测量技术，2023，46（7）：110-116.

[5] ZHANG D，FANG Z Y，WANG Y，et al. Research on an Improved DV-Hop Localization Algorithm based on Psode in WSN [J].Journal of communications，2015，10（9）：728-733.

[6] WANG P，CAI X J，XIE L P. A modified Error-Oriented Weight Positioning Model based on DV-Hop [J].KSII Transactions on Internet and Information Systems，2022，16（2）：405-423.

[7] CHEN T F，SUN L J，WANG Z Q，et al. An Enhanced Nonlinear Iterative Localization Algorithm for DV_Hop with Uniform Calculation Criterion [J/OL].Ad Hoc Networks，2021，111：102327（2020-10-30）.https：//doi.org/10.1016/j.adhoc.2020.102327.

[8] 吴雪敏，张继荣.一种弹簧系数和跳数分类的改进DV-Hop算法 [J].中国科技论文，2020，15（7）：750-754.

[9] 唐德红，王一多，马新国.斯蒂芬森迭代改进DV-Hop的无线传感器节点定位 [J].吉林大学学报：工学版，2022，52（12）：3015-3021.

[10] 刘登峰，章力，邴晓瑛，等.基于布谷鸟差分算法优化的DV-Hop改进算法 [J].系统仿真学报，2017，29（4）：791-797.

[11] 余成成，徐巍，钟宇超，等.基于多通信半径和改进遗传算法的DV-Hop定位 [J].仪表技术与传感器，2023（2）：99-103+120.

[12] 潘志远，卜凡亮.基于蜣螂算法优化的DV-Hop定位算法 [J].电子测量与仪器学报，2023，37（7）：33-41.

[13] 吴建锋，徐振宇，蒋震.无线传感器网络中改进粒子群优化DV-Hop算法的研究 [J].传感技术学报，2022，35（6）：825-830.

[14] NICULESCU D，NATH B. Dv based Positioning in AD HOC Networks [J].Telecommunication Systems，2003，22（1-4）：267-280.

[15] MOHAMMAD D，ZEINAB M，EVA T，et al. Coati Optimization Algorithm： A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems [J/OL].Knowledge-Based Systems，2023，259（2022-11-11）.https：//doi.org/10.1016/j.knosys.2022.110011.

[16] JUNGNICKEL D. The greedy algorithm [J].Graphs，networks and algorithms，1999：129-153.

[17] 余修武，秦晓坤，刘永，等.基于全局人工鱼群算法优化的DV-Hop定位算法 [J].工程科学与技术，2022，54（4）：228-234.

[18] 黄梅根，常新峰.一种基于蒙特卡罗法的无线传感器网络移动节点定位算法研究 [J].传感技术学报，2010，23（4）：562-566.

[19] 时雨农，刘海隆.基于跳数与跳距优化的三维DV-Hop定位算法研究 [J].传感技术学报，2022，35（8）：1080-1085.

[20] CUI L Z，XU C，LI G H，et al. A High Accurate Localization Algorithm with DV-Hop and Differential Evolution for Wireless Sensor Network [J].Applied Soft Computing Journal，2018，68：39-52.

[21] ABD EL GHAFOUR M G，KAMEL S H，ABOUELSEOUD Y. Improved DV-Hop based on Squirrel Search Algorithm for Localization in Wireless Sensor Networks [J].Wireless Networks，2021，27：2743-2759.

作者简介：张潇（2001.01—），女，汉族，河南南阳人，硕士在读，研究方向：无线传感网络；姜金晶（1999.04—），女，汉族，青海西宁人，硕士在读，研究方向：信道估计、深度学习；李新（1962.06—），男，汉族，北京人，教授，博士，研究方向：无线信道建模；通信作者：彭彤（1985.12—）男，汉族，山东济南人，教授，博士，研究方向：无线通信技术。