基于FR4的电磁式扫描光栅微镜结构优化设计

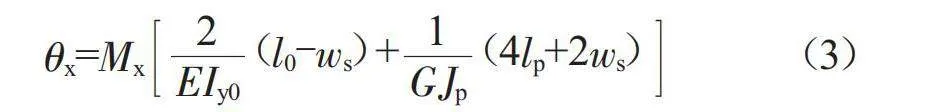
摘要：扫描光栅微镜的转动结构通常设计成扭振系统，通过扭转梁实现微镜转动时的结构抗扭。将扭转梁设计成折叠形式，可以减小扭转梁的抗扭刚度，但扭转振型仍有可能未成为系统的一阶主振型。因此，通过提高系统镜板的转动惯量和设置刚度调节棒，改进系统的振型模态分布。最后，对优化后结构进行了理论计算和基于ANSYS的有限元软件仿真，结果均表明优化后结构能有效改善微镜的扭转谐振特征。

关键词：扫描光栅微镜；结构优化；刚度调节；有限元仿真

中图分类号：TH703" " 文献标志码：A" " 文章编号：1671-0797（2025）03-0044-04

DOI：10.19514/j.cnki.cn32-1628/tm.2025.03.012

0" " 引言

扫描光栅微镜作为微型近红外光谱仪的核心器件，能够同时实现机械扫描与光学分光[1]；具有体积小、功耗低，能以单管探测器代替昂贵的阵列探测器等优点，是替代传统近红外和中红外光谱分析检测装备的新一代核心分光器件[2]。在各种电磁式扫描光栅微镜中，基于FR4的扫描光栅微镜机械结构和驱动线圈可以通过快速、低成本的商业化PCB技术进行加工，传感线圈也可以一体化集成，因此具有显著的低成本优势[3-4]。

1" " 电磁式扫描光栅微镜工作原理

电磁式扫描光栅微镜的电磁驱动器主要是利用驱动电流在磁场中所受安培力来产生驱动力，驱动电压低，驱动位移大且响应速度快。在电磁式扫描光栅微镜中利用多自由度谐振系统特性，实现对扫描光栅微镜转动角的放大，从而有效提升器件扫描角。

基本结构的扫描光栅微镜扭转梁为直梁结构，扭转刚度主要由左右两根扭转直梁提供，假设单根扭转梁的抗扭刚度为Ksθ，FR4制造工艺下扭转梁截面一般为矩形，其高等同镜板厚度t，假定梁宽为ws，则截面扭转因子Jp可由式（1）计算：

Jp=wst3β（1）

式中：β为与ws和t两参数相关的双曲正切函数，具体近似数值也可通过查表得到。

假定扭转直梁的长度为ls，则其扭转刚度Ksθ可由式（2）计算：

Ksθ==（2）

式中：Mx为梁末端施加的扭转力矩；θx为梁末端转角；G为材料的剪切模量。

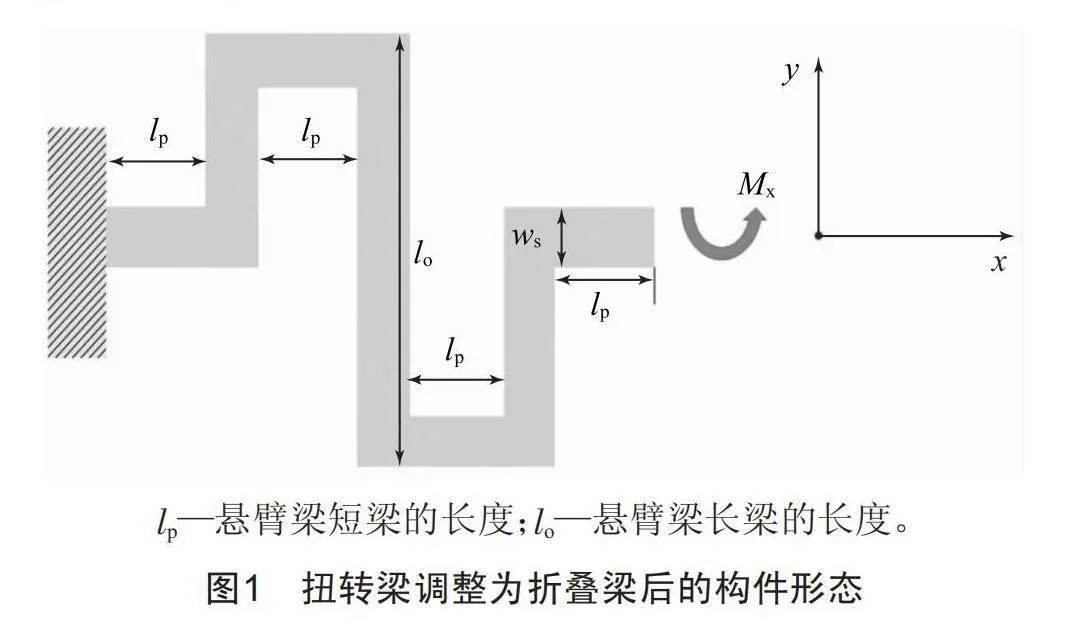
直梁结构微镜系统刚度偏大，会导致谐振微镜偏转角不够大[5]，目前主流的改进方法是将光栅镜板和边框之间的扭转直梁调整为图1所示的折叠梁，以降低扭转梁的扭转刚度。

对于折叠梁结构，其抗扭刚度的计算相对比较复杂，需要根据单元荷载法计算折叠梁末端转角θx与施加的扭转力矩Mx之间的关系，如式（3）所示：

θx=Mx

（l0-ws）+

（4lp+2ws）（3）

式中：E为材料的弹性模量；Iy0为折叠梁矩形截面的惯性矩。

根据式（3）可计算出折叠梁的扭转刚度，如式（4）所示：

Ksθ==

（l0-ws）+

（4lp+2ws）（4）

2" " 优化前结构分析

电磁式扫描光栅微镜的扭转梁由直梁改为折叠梁后将会出现一个严重问题，即微镜沿竖直方向上下振动的抗弯刚度也相应变柔，导致平动模态振型的频率也相应降低，竖直方向上下振动的平动模态可能仍然是系统的一阶主振型，而系统期望的扭转振型未必会变成一阶主振型。一般来说，低阶振型对结构振动的影响要大于高阶振型，因此扭转振型不是第一阶主振型对以扭转发生谐振为工作目标的微镜系统而言不够理想[6]。

首先，建立折叠梁扫描光栅微镜模型参数。FR4镜板基底尺寸：12 mm×12 mm×0.4 mm；折叠梁尺寸：l0=12 mm、lp=0.7 mm、ws=1.2 mm；密度：1 850 kg/m3；杨氏模量：20 GPa；剪切模量：7.8 GPa。FR4镜板基底上叠合光栅层，光栅层材料密度：2 330 kg/m3；杨氏模量：169 GPa；剪切模量：66 GPa。理论计算结果显示，器件一阶模态的振型为微镜沿竖直方向上下振动，谐振频率为294.1 Hz，二阶模态振型即为预期的微镜扭转运动，谐振频率为295.3 Hz，三阶和四阶模态的振型分别为微镜在其所在平面内的扭转运动和平动，谐振频率分别为712.9 Hz和814.1 Hz。可以发现器件预期工作模态与相邻模态间的谐振频率相隔较近，存在一定的发生振型跳跃的概率；另外，扭转振动并非第一阶主振型，工作时容易受到一阶主振型成分的影响，引起模态间的串扰。

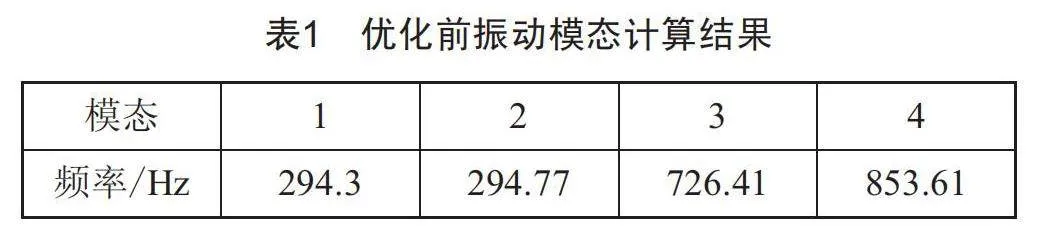
同时，应用ANSYS有限元软件对结构优化前的折叠梁扫描光栅微镜结构进行模态分析。结构优化前的第一阶振动模态和第二阶振动模态分别如图2、图3所示，振动频率结果如表1所示。

可以发现第一阶为竖直方向上下平动，谐振频率为294.3 Hz，二阶模态振型为期望的微镜扭转运动，谐振频率为294.77 Hz。仿真结果和理论计算结果一致，均表明一阶和二阶模态谐振频率相距很近，极易发生模态间的串扰。

3" " 结构优化设计

结构优化目标：一方面提高微镜系统的转动惯量，但避免提高系统的抗扭刚度；另一方面大幅提高微镜系统在竖直上下方向的抗弯刚度。这样优化设计后，可以拉开微镜系统一阶和二阶振型的频率间隔；同时，将扭转振型调整为微镜系统的第一阶主振型。优化后结构如图4所示。第一，在FR4镜板基底一对侧边各增加一条附重棒，针对性提高微镜系统的转动惯量；第二，安装一端可在椭圆孔支座内自由转动但上下方向约束的一对刚度调节棒，提高微镜系统在竖直上下方向的抗弯刚度，但不改变抗扭刚度。

接下来，对本文所提的优化结构进行计算仿真。为降低计算难度，简化调节棒的截面并调整布置位置，同时椭圆支座的约束在ANSYS中被设定为转动约束释放，而仅在竖直上下方向限制位移。第一阶模态如图5所示，显示系统的第一阶振型是扭转振型，位于扭转轴中轴线上的刚度调节棒由于在两端支座处释放了转动约束（可自由转动），微镜转动时圆杆调节棒不会在系统中形成抗扭贡献；从分布云图上也可以看出圆杆确实满足了设计要求，只有转动但未受扭矩，因此圆杆也就没有因为需要抵抗扭矩所形成的应变和应力。

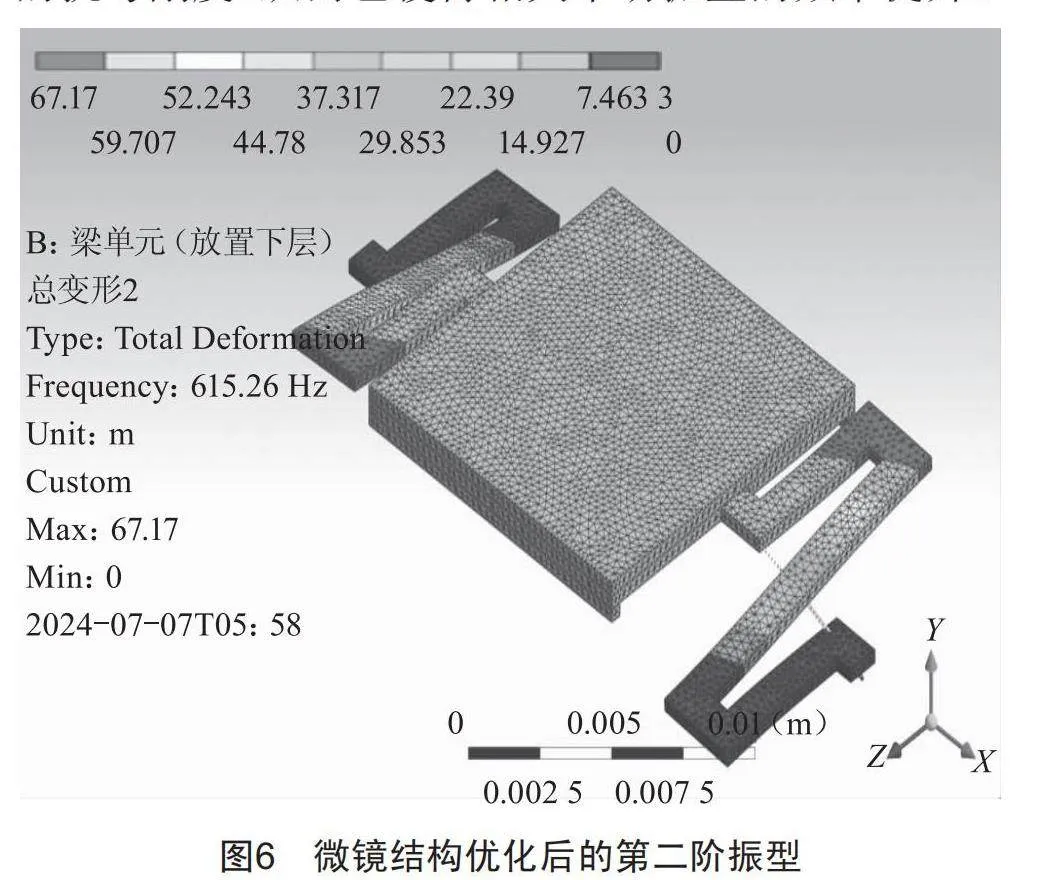
第二阶振型为竖直方向的上下平动模态，如图6所示。在这个方向上可以看到圆杆状刚度调节棒存在明显的挠曲变形，证明相关构造设计在竖直方向上提供了有效抗弯刚度，增加了该平动方向整个系统的抗弯刚度，从而也使得相关平动振型的频率提升。

优化后振动频率结果如表2所示。

由表2可以发现，结构优化后确保了所期望的扭转振动模态为第一阶主振型（谐振频率为262.16 Hz），而竖直方向上下平动模态变为第二阶振型（谐振频率为615.26 Hz），这将增加平动振型模态的启动和激发难度，削减系统工作过程中并不期望的平动振型振动分量；同时，结构优化后系统的第一阶主振型扭转振动的频率与其他各阶振型频率也清晰分离，几乎不可能发生模态间的串扰或振型跳跃，从而构建了更可靠的扭转谐振系统。

4" " 结束语

本文针对FR4电磁式扫描光栅微镜系统可能出现的扭转振型频率并非第一阶主振型的结构失调现象，设计了增加附重棒和刚度调节棒的优化结构。根据ANSYS有限元软件的仿真计算结果，设计能有效调整系统的振型分布，使期望的扭转振型成为系统的一阶主振型，同时优化后的结构也显著拉开了系统的一、二阶频率差值，确保能清晰分离不同振型，避免发生频率跳跃，从而有效放大了微镜系统所追求的扭转谐振特征，提高了系统工作的可靠性。

[参考文献]

[1] 庾繁.电磁式MOEMS扫描光栅微镜控制系统研究[D].重庆：重庆大学，2020.

[2] 尹欣慧，顾雯雯，张青莲.电磁式MOEMS扫描光栅微镜驱动系统优化设计[J].微纳电子技术，2023，60（2）：251-258.

[3] 周原媛，袁幸权，温泉，等.基于FR4的多自由度电磁式扫描光栅微镜结构设计[J].遥测遥控，2023，44（4）：109-116.

[4] HAN A，CHO A R，JU S，et al.Electromagnetic biaxial vector scanner using radial magnetic field[J].Optics Express，2016，24（14）：15813-15821.

[5] 尹欣慧.电磁式MOEMS扫描光栅微镜封装结构设计及性能测试[D].重庆：西南大学，2023.

[6] 雷宏杰.高性能低成本微型集成扫描光栅微镜关键技术研究[D].重庆：重庆大学，2019.

收稿日期：2024-10-11

作者简介：刘海涛（1975—），男，重庆人，博士研究生，研究方向：MEMS器件设计及应用。