打破“圆”规轮胎并不是非“圆”不可
2025-02-20彭子妤王天志
在我们的日常生活中,无论是汽车、飞机,还是用来运送货物的推车,它们的轮胎都是圆形的。为什么会将轮胎设计为圆形?这利用了圆形的什么特殊性质?其他形状是否也可以“变身”为轮胎外形?接下来就和我们一起从数学角度探秘这些问题吧。
圆形为何备受青睐?
物理优势——圆形轮胎可以最大限度地减少轮胎与地面的接触面积,从而减小摩擦力,节约前进过程中的能源消耗,保障汽车等交通工具平稳、安全地行驶。
圆形的半径是确定的,其圆心到圆周任意一点的距离都相等,所以当轮胎在地面滚动时,轮胎中心与地面的距离总是等于车轴——即轮胎半径,使车辆行驶起来极为平稳。
在了解圆形轮胎背后的原理后,我们就可以大胆想象:世界上是否有其他图形能够满足轮胎必备的平稳性?若能找到另外能满足“图形中心与地面接触任意一点的距离都相等”的图形,设计师们就可以设计出其他形状的轮胎。
现实中,确实有一种非圆形形状的轮胎,它似三角形又似圆形,能支持自行车的使用。在数学世界里,我们把这样的图形称为鲁洛克斯(Reuleaux)三角形,又称为莱洛三角形、圆弧三角形。

似圆又非圆
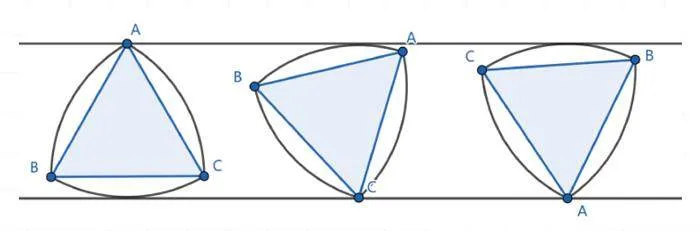
鲁洛克斯三角形是一个独特的三角形。它是一个以正三角形的顶点为中心、以边长为半径构建3段圆弧后,由这3段圆弧组成的“曲边三角形”。
我们先画出一个正三角形ABC,再以正三角形ABC的3个顶点为圆心、以其边长为半径画弧,便可以得到一个鲁洛克斯三角形。
根据其画法和特征,我们可以分析出它具备圆的等距性。
当鲁洛克斯三角形向任意方向转动时,作与它运动轨迹相切的两条平行直线,可以发现所作出的每组平行线都有相同的宽度。在数学上,这类在平面内按一定规律旋转一定角度后,仍能与原线段逆向重合的特殊几何图形,被命名为等宽曲线。
而这组平行线间的垂线段被称为等宽曲线的宽。鲁洛克斯三角形正是等宽曲线的一种,它能在两条平行的直线(该直线与正三角形边长相等)间自由滚动,距离与其圆弧半径相等,并与这两条平行线始终保持接触。

圆形是等宽曲线中最常见的一种,根据等宽曲线的定义可以发现,任意一个具有奇数边,且对角线相等而边长不一定相等的多边形,都可以构造出等宽曲线,而偶数边的多边形已被证明是不可能构造出等宽曲线的。例如,以正五边形的对角线为半径画5段圆弧,就能得到一个圆弧五边形,还可以根据等宽曲线定义作出圆弧七边形、圆弧九边形等各种正多边形的等宽曲线。
“玩转”等宽曲线
那么,任意多边形能否得到对应的等宽曲线呢?以直角三角形为例,我们一起来探究一下它是否存在对应的等宽曲线。
首先画出一个具有勾三股四弦五特征的直角三角形,即直角三角形斜边AB=5,较长直角边AC=4,较短直角边BC=3,便于作辅助线。
随后,根据等宽曲线定义中的等宽性,分别以3个顶点为圆心,延长直角三角形的边长,使得延长后的相邻两条边可成为一个圆的两条半径。

①延长BC至F,可将AB、BF看作一个圆的半径;
延长CB至G,可将AC、CG看作一个圆的半径;
延长AB至D、AC至E,可将AD、AE看作一个圆的半径
②所以AB=BF=5" AC=CG=4" AD=AE
使得CF=CE=AB-BC=2 使得BG=BD=AC-CB=1
③由此就可以得到:
AD=AE=AB+BD=5+1=6
最后,分别以C为圆心,以CF为半径作从E到F的圆弧;
以B为圆心,以BA为半径作从F到A的圆弧;
以C为圆心,以CA为半径作从A到G的圆弧;
以A为圆心,以AD为半径作从D到E的圆弧;
以B为圆心,以BG为半径作从G到D的圆弧;
得到5条圆弧,符合等宽曲线定义。
由此我们可以发现,只需要根据等宽曲线的定义,就可以构造出任意奇边形对应的等宽曲线。
鲁洛克斯三角形“动起来”
那么,在平面中存在的等宽曲线是否在多维空间中存在立体形态呢?根据平面上鲁洛克斯三角形的画法,我们首先可以在立体空间里构建一个正四面体,以各个顶点为球心以及对角线为半径构建球体,而中心的“圆润四面体”便是正四面体的三维定宽体——Meissner体,中文名称为迈斯纳四面体。
等宽曲线的独特价值
由于具有等比例对称美感、可分散力的工程学优势、节约空间优势及其他特殊性质,等宽曲线在数学或设计等方面具有极高的研究价值。
例如,在研究最值问题时,高度相同的等宽曲线具有相同的周长(等宽曲线的周长公式为:宽度×π),在等宽曲线中,圆的面积最大,鲁洛克斯三角形的面积最小。
鲁洛克斯三角形凭借其滚动性质,还可以作为运动学问题中的曲线连杆。不仅如此,在设计方面,大到国家货币,小到扑克牌的创新,都有鲁洛克斯三角形的身影。
英国以圆弧七边形为灵感,设计了50便士与20便士的硬币,这样的硬币给人一种圆润且不失比例的美感。
有研究人员还根据鲁洛克斯三角形的边、角均圆润的特点和人体工学知识,设计出了更方便人们使用的扑克牌,使它的弧度与握牌时手掌内部的结构相吻合。相比于传统扑克牌的长方形造型,新型扑克牌尖角朝下的抓牌方式,使得扑克牌在手中的抓握面积更小,更加美观。
等宽曲线是一类好看且有趣的几何图形,希望各位青少年可以充分发挥想象力和创造力,动手尝试构造自己喜爱的等宽曲线。
知识拓展
鲁洛克斯三角形让钻头变得更好用
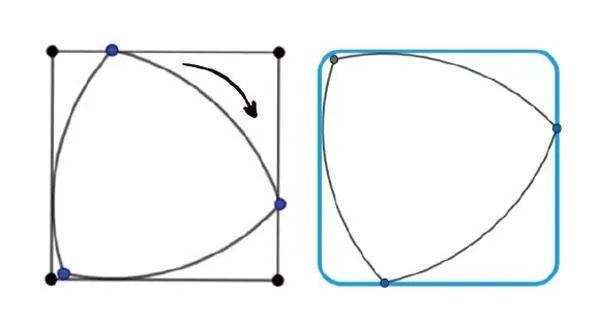
德国机械学家莱洛在设计方孔钻头时发现了鲁洛克斯三角形,并凭借这个灵感发明创造出了方孔钻头。
固定了鲁洛克斯三角形钻头后,钻头开始在一个边长为鲁洛克斯三角形的正方形内旋转工作。莱洛发现,这个三角形在任何时候都有4个点可与正方形接触,且这4个点的位置是不断改变的,在旋转之后可以获得一个四角圆润的正方形孔洞。
运用五边形钻头则能得到正六边形的钻孔,这可以满足一些特殊的工业设计需求。

(责任编辑 / 王佳璇 美术编辑 / 徐博宇)
