城市环卫车垃圾收运调度系统优化

摘要： 为了提高城市环卫车垃圾收运调度效率和降低总成本，基于环卫车参数、 道路状况等模型假设，建立城市环卫车垃圾收运调度系统数学模型，并提出城市环卫车垃圾收运调度系统优化方案； 通过应用节约算法得到行驶总路程最小的子路径集合，将子路径任务合理分配给所有环卫车，以达到行驶总路程最小和任务均衡性最高的任务分配优化目标； 以济南市市中区10个环卫区域道路网络的环卫车实际调度数据作为算例，综合评估所提出的系统优化方案，分析所提出系统优化方案的可行性和有效性。结果表明： 与以顺序优先原则调度分配的优化前方案相比，利用所提出的系统优化方案分别进行中小型、 大型环卫区域道路网络的环卫车垃圾收运调度，所需环卫车辆数分别减少39.03%、 18.78%，环卫运营成本分别降低约2.8×104、 5.05×104元，平均行程利用率分别达到97.4%、 93.6%，不仅可以显著降低环卫经济成本，而且能够极大地提高环卫车的作业效率； 在同等任务量时，利用所提出的系统优化方案分配任务，环卫车配置数量减少3辆，任务分配优化程度提高到85.16%，实现了环卫车之间的任务均衡，从而带来良好的经济和社会效益。

关键词： 环卫车调度； 垃圾收运； 调度系统优化； 节约算法； 任务均衡

中图分类号： TP301.6

文献标志码： A

开放科学识别码（OSID码）：

Waste Collection and Transportation

Scheduling System Optimization of Urban Sanitation Vehicles

FENG Fuqiang LIU Haining LI Fajia ZHANG Liu2， CHENG Yifei2

（1. School of Mechanical Engineering， University of Jinan， Jinan 250022， Shandong， China;

2. Jining Antai Mine Equipment Manufacturing Co.， Ltd.， Jining 272300， Shandong， China）

Abstract： To enhance" waste collection and transportation scheduling efficiency of urban sanitation vehicles and reduce the total cost， a mathematical model of waste collection and transportation scheduling system for urban sanitation vehicles was established on the basis of model assumptions such as sanitation vehicle parameters and road conditions. An optimization scheme for the waste collection and transportation schedulingsystemofurbansanitationvehicleswasproposed.Byapplying saving algorithm， sub-paths with the smallest total driving distance were obtained， and the sub-path tasks were allocated to all sanitationvehiclesrationallytoachieve optimizationgoalsofminimizingtotaldrivingdistanceandmaximizingtaskequilibrium. Taking actual scheduling data of sanitation vehiclesin10sanitationarearoadnetworksinShizhongDistrict ofJinan City as an example， the proposed system optimization schemewascomprehensivelyevaluatedtoanalyze itsfeasibilityandeffectiveness.Theresultsshowthatcomparedwiththeschemebeforeoptimizationusingsequencepriority principle for scheduling allocation， using the proposed system optimization scheme for waste collection and transportation scheduling of sanitation vehicles in medium and small， as well as large-scale urban sanitation areas， numbers of sanitation vehicles required are respectivelyreducedby39.03%and18.78%，sanitationoperationcostsarerespectivelyreducedbyapproximately2.8×104yuanand5.05×104yuan，andaverageoperationmileage rates respectively reach 97.4% and 93.6%，whichcannotonlysignificantlyreducesanitationeconomiccosts，but also greatly improve operational efficiency of sanitation vehicles. When performing task allocation using the proposed system optimization scheme under the same task amount， the number of sanitation vehicles is reduced by 3 units， and the task allocation optimization degree is increased to 85.16%. Task equilibrium among sanitation vehicles is realized， thereby bringing good economic and social benefits.

Keywords： sanitation vehicle scheduling; waste collection andtransportation;schedulingsystemoptimization;savingalgorithm; task equilibrium

随着我国城镇化水平不断提高，人们对城市卫生环境有了更高的诉求，环卫需求不断提升，但是人力成本的不断上升以及人工清扫效率低的缺点使得城市路面的清扫工作已由传统的人工清扫向高效率的机械化清扫转变。尽管近年来机械化环卫车的配置与调度取得了一定的进展，但是在许多城市，因缺乏科学、合理的调度方案以及过度依赖市政管理人员的主观经验而导致环卫车资源浪费以及调度不合理。如何科学、 合理地配置和调度环卫车以满足环卫工作的需要，已成为交通工程领域中的一个热门研究方向。

环卫车调度实质上属于车辆路径问题（vehicle routing problem，VRP）^［1］，解决此类问题的方法以启发式算法为主。Wu等^［2］提出将设施选址与路径优化相结合，并利用结合粒子群算法与模拟退火算法的混合算法寻找低碳车辆路径问题的最优解，结果表明，该混合算法在求解过程中能有效平衡全局、 局部搜索的能力，从而在减少碳排放的同时，降低了传统的废物管理成本； Tirkolaee等^［3］通过分析垃圾收集点的分布建立了多目标环卫车优化模型，使用田口设计（Taguchi design）方法优化多目标入侵杂草算法参数，结果表明，参数优化后的多目标入侵杂草算法在求解城市垃圾收集问题时具有较高的效率和准确性； Jian等^［4］深入探讨了具有枢纽港靠岸时间限制的船只航线规划和货物流通协调问题，建立了精确的定价模型与基于列的启发模型，结果表明，这2种模型均能在合理的时间内确定高质量的解决方案，有效降低了运营、 转运连接成本； 陈彦等^［5］结合环卫设施的选址与环卫车的行驶轨迹，建立混合整数线性规划（mixed integer linear programming， MILP）模型，优化城市生活垃圾收运线路，结果表明，通过该模型设计的收运线路可以有效缩短车辆的行驶距离，从而减少油耗和尾气排放，对改善居民生活环境质量具有积极作用； 为了尽可能缩短甩挂运输的行驶时间，边展等^［6］提出了一种新的带时间窗的甩挂运输路径优化模型，同时利用两阶段融合优化算法，使该优化模型在符合各种限制条件的前提下，最大程度地满足目标函数。

国内外学者从不同角度探索了各种车辆路径问题解决方法^［7］，但是目前关于城市环卫车垃圾收运调度问题的研究较少。本文中针对城市环卫车调度系统优化问题，基于环卫车参数、 道路状况等模型假设建立数学模型，提出城市环卫车垃圾收运调度系统优化方案（简称系统优化方案）； 利用节约算法求出满足环卫车续航路程约束的最佳子路径，并将这些子路径任务合理分配给环卫车； 利用济南市市中区10个环卫区域道路网络的环卫车实际调度数据综合评估所提出的系统优化方案，分析所提出系统优化方案的可行性和有效性。

1 数学建模

1.1 模型假设

在建立城市环卫车辆路径组合模型时， 通常须作出一些假设， 以简化问题和使模型更易于求解^［8］。 为了给城市环卫车垃圾收运调度系统数学模型的构建奠定良好的理论基础， 本文中提出以下假设： 1）环卫车参数相同，如油耗、 载重等； 2）道路状况良好，无堵车现象； 3）环卫车辆基地固定； 4）环卫车在行驶过程中保持相同的速度。

假设有n个工作点、 c辆环卫车， 分别用集合F={1，2，…，n}、 A={1，2，…，c}表示。规划每辆环卫车的作业任务，使得环卫车从环卫区域道路网络内给定节点出发，遍历规定的作业路段而完成作业任务。约束条件如下： 每个工作点都满足服务次数m； 环卫车的最大续航能力为Q，每条子路径的行驶距离小于环卫车的最大续航路程； 环卫车行驶过程中保持相同速度； 环卫车辆可由环卫区域道路网络出发节点进入，在终止节点退出。最终目标有3个： 1）所需环卫车辆数最少； 2）所有环卫车行驶总路程最小； 3）每辆环卫车之间的任务量差异最小。

1.2 模型建立

根据模型假设，建立城市环卫车垃圾收运调度系统数学模型为

min∑k∈A∑i∈F∑j∈Fdijxijk ，（1）

min∑k∈A∑j∈Fx1jk ，（2）

min∑ck=1∑i∈Fxijk-nc2 ，j∈F ，（3）

s.t.∑k∈A∑j∈Fxijk=m，i∈F ，（4）

∑i∈F∑j∈Fdijxijk≤Q，k∈A ，（5）

∑j∈Fx1jk=1，k∈A ，（6）

∑i∈Fxihk-∑j∈Fxhjk=0，h∈F，k∈A ，（7）

∑i∈Fxink=1，k∈A ，（8）

xijk∈{0，1}，i， j∈F，k∈A ，（9）

式中： dij为环卫车从工作点i到工作点j的路程； xijk为环卫车k是否从工作点i行驶到工作点j的判断结果，如果环卫车k在工作点i完成工作后直接开往工作点j，则xijk=1，否则xijk=0； h为模型中某个特定的工作点。

式（1）、 （2）、 （3）分别保证了3个最终目标，即所有环卫车行驶总路程最小所需环卫车辆数最少、每辆环卫车之间的任务量差异最小。式（4）表示每个工作点满足服务次数约束。式（5）表示所有环卫车都满足最大续航能力约束。式（6）、 （7）、 （8）保证环卫车从出发节点进入，完成任务后，由终止节点退出。式（9）为整数化约束。

例如，给定10个工作点，则可以用3个整数序列R1、 R2、 R3表示环卫车子路径方案。根据运营效率的需求，对环卫车1、 2分配任务，其中环卫车1将沿路线R3运行，环卫车2沿路线R2—R1运行。

2 系统优化方案

根据所建立的城市环卫车垃圾收运调度系统数学模型，提出城市环卫车垃圾收运调度系统优化方案，即通过节约算法得到行驶总路程最小的子路径集合，然后通过任务分配优化找到任务均衡性最高的任务分配方案，最终实现系统优化。

2.1 节约算法原理

节约算法（saving algorithm）又称C-W算法或节约里程算法^［9］，是一种启发式算法，旨在解决车辆路径问题^［10］，在物流领域中占有重要地位。该算法的基本原理是依次将路径规划问题中的2个回路合并为1个回路，从而最大限度地缩短总距离，直至达到车辆的最大续航能力； 通过不断地迭代、 优化，直到满足目标需求^［11］。

将n个不同目的地中的每个目的地看作1个节点，并以其中某个节点作为起点。例如，以第1个节点为起点。将所有节点与起点相连，构成线路1—j—1（j=2，3，…，n），获得含n-1条线路的图。沿该线路行驶至n个目的地的总距离为

z=∑nj=2C1j ，（10）

式中C1j为节点1到节点j线路的路程。假设C1j=Cj1，当将节点i与节点j相连，通过节点i至节点j的弧形路线时，产生的路程节约值^［11］为

s（i， j）=C1i+C1j-Cij 。（11）

对于所有的节点对（i， j），应优先考虑将通过节点i至节点j的弧形路线时所产生路程节约值较大的弧插入线路。

2.2 节约算法步骤

由节约算法原理可得

s（i， j）=di0+d0j-dij ，（12）

式中di0、 d0j分别为起始点0与工作点i、 j之间的距离。

计算连接点i、 j后的路径长度与i、 j分别位于不同路径时路径长度之间的差值， 即路程节约值s（i， j）。 当选择连接点i、 j的路径时，必须满足环卫车的续航能力约束。

节约算法步骤如下：

步骤1 令M={s（i， j）s（i， j）gt;0}为所有s（i， j）gt;0组成的集合，该集合含有全部有意义的s（i， j）。对M中的元素s（i， j）由大到小排序，得到递减的有序集合，即s（i， j）最大的元素排在最前面。该排序用于确定任务分配的顺序，先分配s（i， j）较大的任务，然后依次分配s（i， j）较小的任务。

步骤2 令元素为i、 j的集合U含有全部可供选择的待工作点对。

步骤3 如果M为空集，则执行步骤5； 否则，检查M的第1个元素s（i， j）及端点i、 j，如果i、 j均不位于已构建的路径，或者i、 j中至少有1个位于已构建的路径但非路径内点，或者i、 j位于已构建的不同路径但均是端点而非内点，则执行步骤4； 否则，执行步骤5。

步骤4 当i、 j相连后的路径总长度q小于或等于规定值Q时，执行步骤5。如果q大于规定值Q，则须重新选择其他路径或调整任务分配或环卫车路线，即执行步骤5，以确保行驶总路程不超过规定值Q。连接i、 j，令U=U-{i， j}，执行步骤5。

步骤5 从集合U中去除元素i、 j，执行步骤3； 如果U为空集，则算法停止； 否则，将剩余的元素划分为子路径并继续执行算法。算法在不断处理子路径的过程中持续执行，直到所有的路径都被处理完毕或U为空集为止。

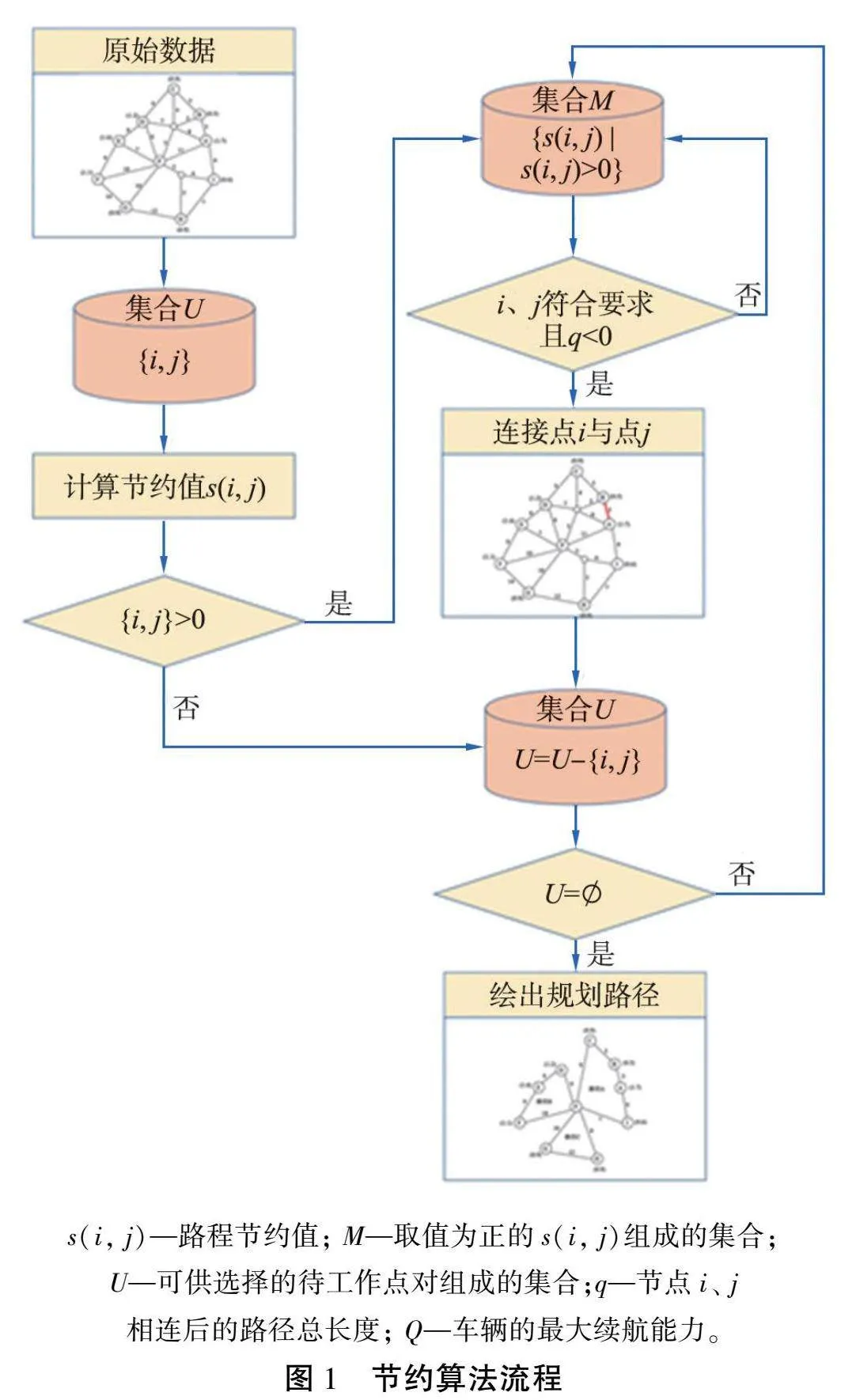
节约算法流程如图1所示。

2.3 任务分配优化

尽管节约算法能找到行驶总路程最小的子路径集合；但是同一辆环卫车在不同时间段内重复使用可以节省大量的时间和资源，因此为了在任务分配和环卫车调度中既能使所需环卫车辆数最少，又能满足各环卫车所负责的任务量尽可能平均，还须制定最优的任务分配方案。

2.3.1 任务分配优化程度

任务分配优化程度指的是在任务顺利完成的前提下，通过合理的任务分配和调度，尽可能地使每辆环卫车所负责的任务量相对平均，从而提高任务分配的效率和公平性。本文中的任务分配优化程度通过计算每辆环卫车完成的工作点个数评估任务分配的效果和调整任务分配方案。在实际应用中，任务分配优化程度是任务分配和环卫车调度策略的重点考虑因素之一，可以通过不断地优化任务分配方案，提高任务分配的效率和公平性。

定义任务分配优化程度为

θ=1-∑ck=1Tk-TavgTtot ，（13）

式中： Tk为环卫车k完成的工作量； Ttot为总任务量； Tavg为平均任务量， Tavg=Ttot/c。

为了实现环卫车任务的均衡分配，应满足以下2个条件： 1）服务开始时间越早，即子路径任务开始越早，则越优先被分配； 2）对所有环卫车辆增加任务量约束，并设置任务量约束阈值λ，确保工作量不超过λ。

2.3.2 任务分配优化步骤

任务分配优化步骤如下：

步骤1 对于给定的子路径方案集合R，根据路径上的任务和任务对应的处理时间，得到第l个子路径任务的开始时间ts（l）、 结束时间te（l）。

步骤2 令任务量约束阈值λ=Tavg，首先按照子路径的开始工作时间ts（l）从小到大的顺序对子路径方案Rl排序，然后设定环卫车辆数c的初始值为1。

步骤3 分割子路径方案集合R，把前c个子路径任务分配给c辆环卫车，并将前c个子路径任务作为每辆环卫车的首个任务。

步骤4 遍历每辆环卫车的任务列表， 记录te（l）， 然后在所有满足te（l）gt;ts（l）的待分配子路径中， 找到ts（l）最小的子路径作为该环卫车的下一个子路径任务。 重复该步骤， 直到不存在起始时间大于该环卫车最后1个子路径终止时间的待分配子路径。

步骤5 如果执行任务分配的步骤后， 仍有子路径任务没有被分配至环卫车辆， 则将环卫车辆数加 即c=c+ 然后重新回到任务分配的步骤3， 直到所有任务都分配完成； 如果执行任务分配的步骤后， 所有子路径任务都已分配至环卫车辆， 则至少需要c辆环卫车才能完成所有任务，执行步骤6。

步骤6 基于步骤5中的c值，设定任务量约束阈值λ的约束条件，并重新执行步骤2。如果所有子路径方案都已被分配，则算法停止执行；否则，增加λ的值，并返回步骤6。

任务分配优化流程如图2所示。

3 算例分析

3.1 研究区域

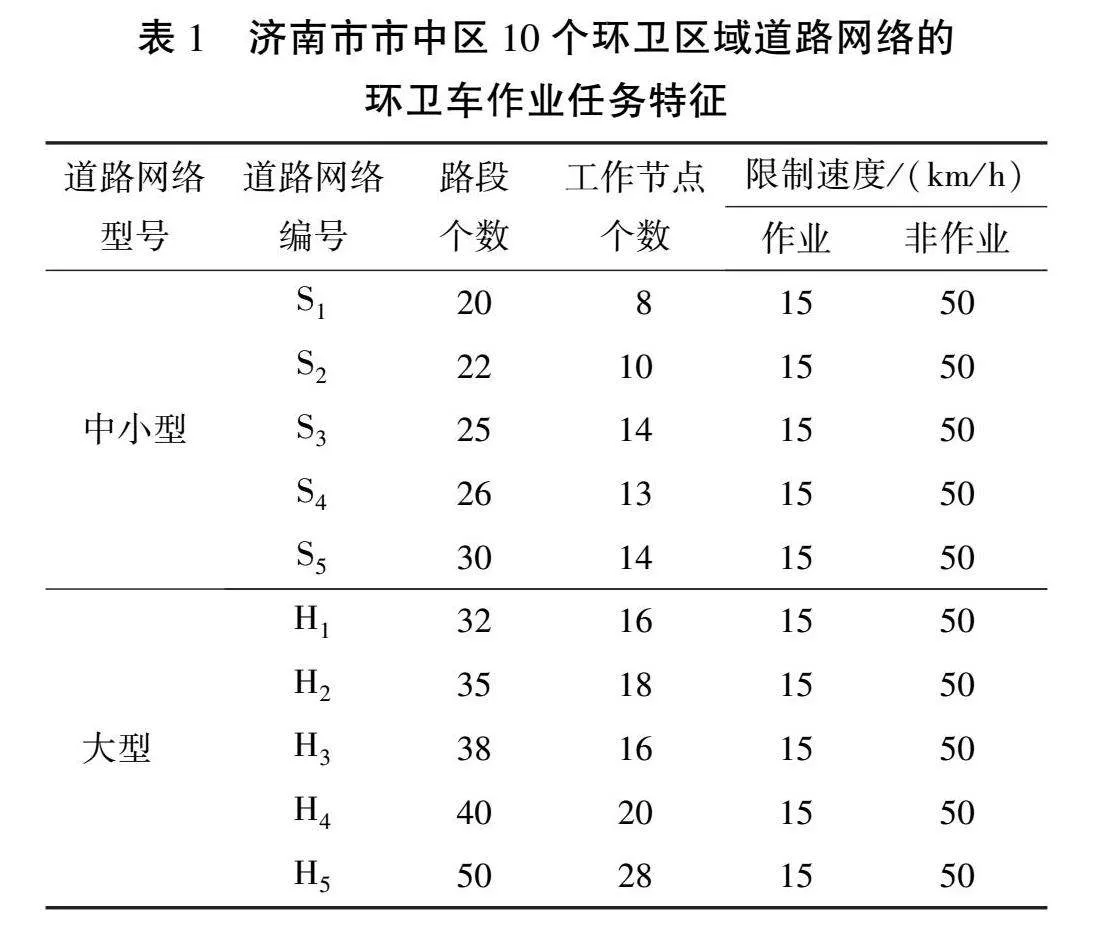
以济南市市中区10个环卫区域道路网络的环卫车调度数据作为算例，验证所提出系统优化方案的有效性。根据研究区域中的路段个数和工作节点个数，将10个环卫区域道路网络划分为中小型、 大型环卫区域道路网络^［12］。表1所示为10个环卫区域道路网络的环卫车作业任务特征。中小型、 大型环卫区域道路网络各5个，编号分别为S1、 S2、 …、

S5， H1、 H2、 …、 H5；中小型环卫区域道路网络的路段个数小于30且工作节点个数小于15，大型环卫区域道路网络的路段个数大于30且工作节点个数大于15。

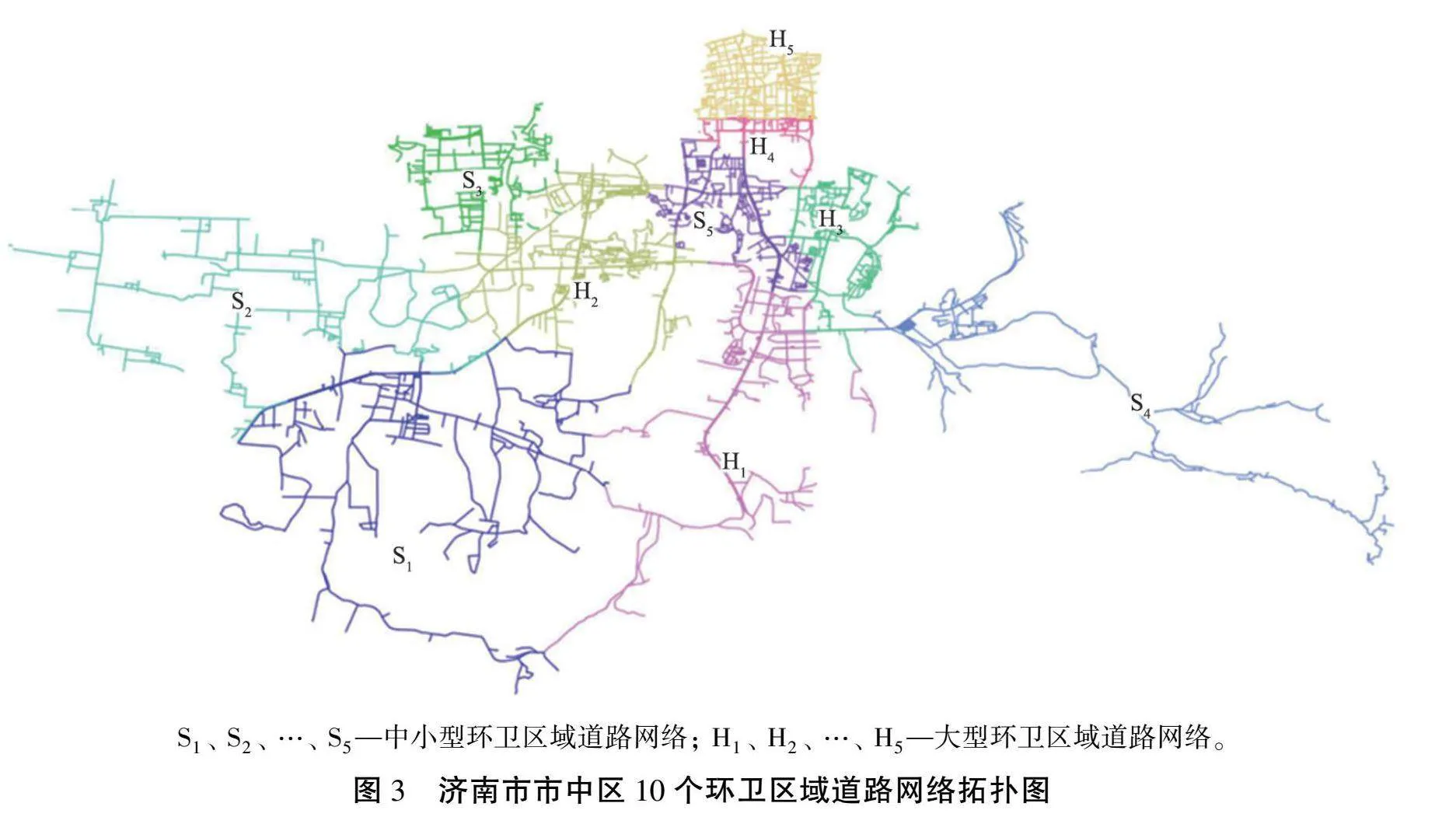
为了获取研究区域的道路网络拓扑，利用全球公共领域地图数据集获取网站Natural Earth提供的免费地理信息数据文件，获取济南市市中区环卫区域道路网络的详细信息，经过数据分析、 信息提取及预处理，形成具有结构性的道路网络节点及路段相关数据，并利用QGIS软件实现道路网络数据导入、 拓扑规则创建、 拓扑检查、 拓扑错误修复和拓扑关系可视化，10个环卫区域道路网络拓扑图如图3所示。

3.2 结果与分析

3.2.1 评估指标

从经济成本、 作业效率、 任务分配均衡性3个方面与以顺序优先原则调度分配的优化前方案比较，评估所提出系统优化方案的优化效果。在经济成本方面，以运营成本作为评估指标； 在作业效率方面，以行程利用率作为评估指标； 在任务分配均衡性方面，以任务分配优化程度作为评估指标。

环卫车的运营成本包括环卫车购置成本和环卫车出行成本，其中环卫车出行成本取决于环卫车行驶总距离与单位作业成本乘积的累加值。定义运营总成本为

P=apv+∑ak=1∑bo=1lkopr， a∈瘙綄+， b∈瘙綄+，（14）

式中： a为道路网络所用环卫车辆数； b为路段总个数； pv为购置成本； pr为平均行驶成本； lko为环卫区域道路网络上环卫车k在路段o的行驶总路程。

行程利用率E是环卫车在完成任务时，环卫车工作状态下行驶的总路程L1与实际完成任务所需的总路程L2之比，即

L1=∑ak=1∑bo=1l^ko" ，（15）

L2=∑ak=1∑bo=1lko ，（16）

E=L1L2×100% ，（17）

式中l^ko为环卫区域道路网络中环卫车k在工作状态下行驶通过路段o所需的总路程。如果E增大， 则环卫车的作业效率提高， 相应的调度方案更合理。

根据式（13）， 任务分配优化程度θ越大， 则任务分配方案效果越好， 各环卫车之间的任务差异越小。

3.2.2 优化前、 后方案对比

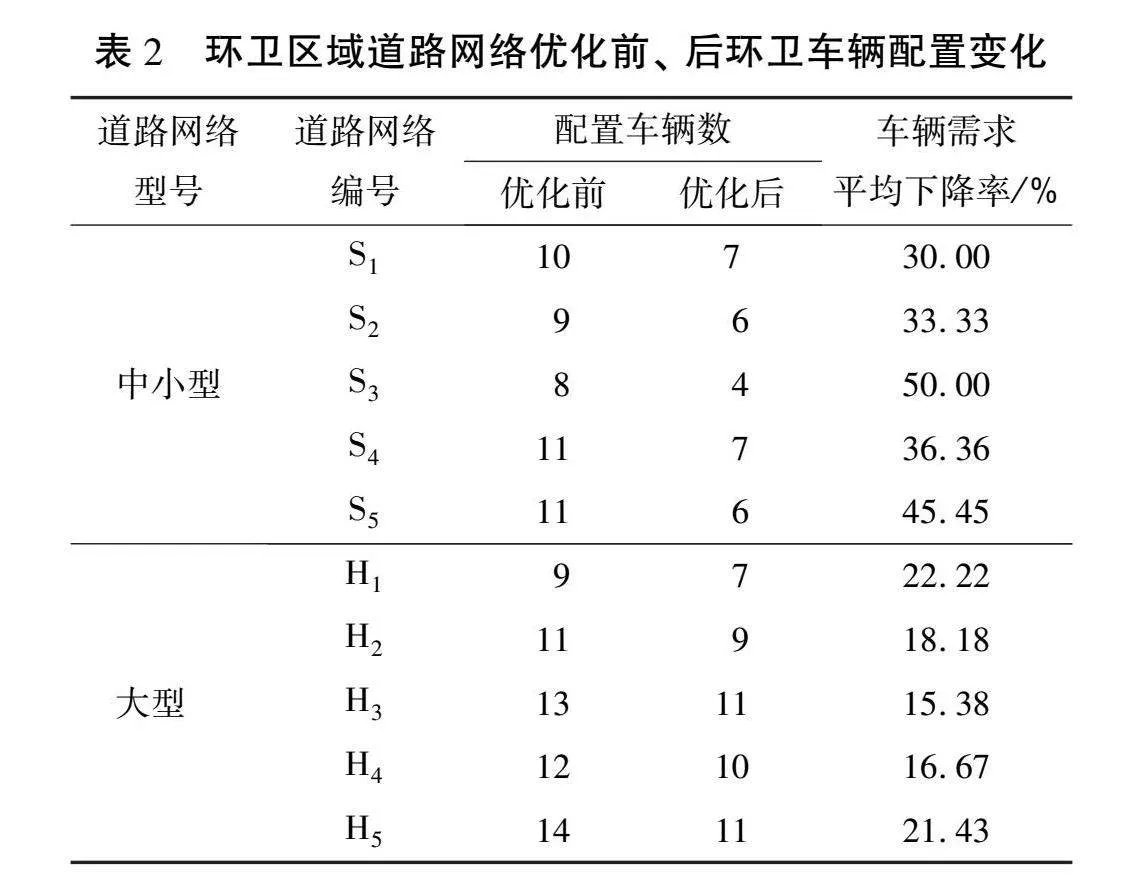
表2所示为环卫区域道路网络优化前、 后环卫车辆配置变化。 由表可知： 所提出的系统优化方案优化后所需环卫车辆数显著减少。 在中小型环卫区域道路网络中， 环卫车辆需求平均下降率为39.03%，其中环卫区域道路网络S3、 S5的环卫车辆需求平均下降率分别减少50.00%、 45.45%，优化效果最明显； 大型环卫区域道路网络的平均下降率为18.78%，其中优化效果最显著的是H1，环卫车辆需求平均下降率为22.22%。由此可知，所提出的系统优化方案有效地节省了环卫车辆资源。

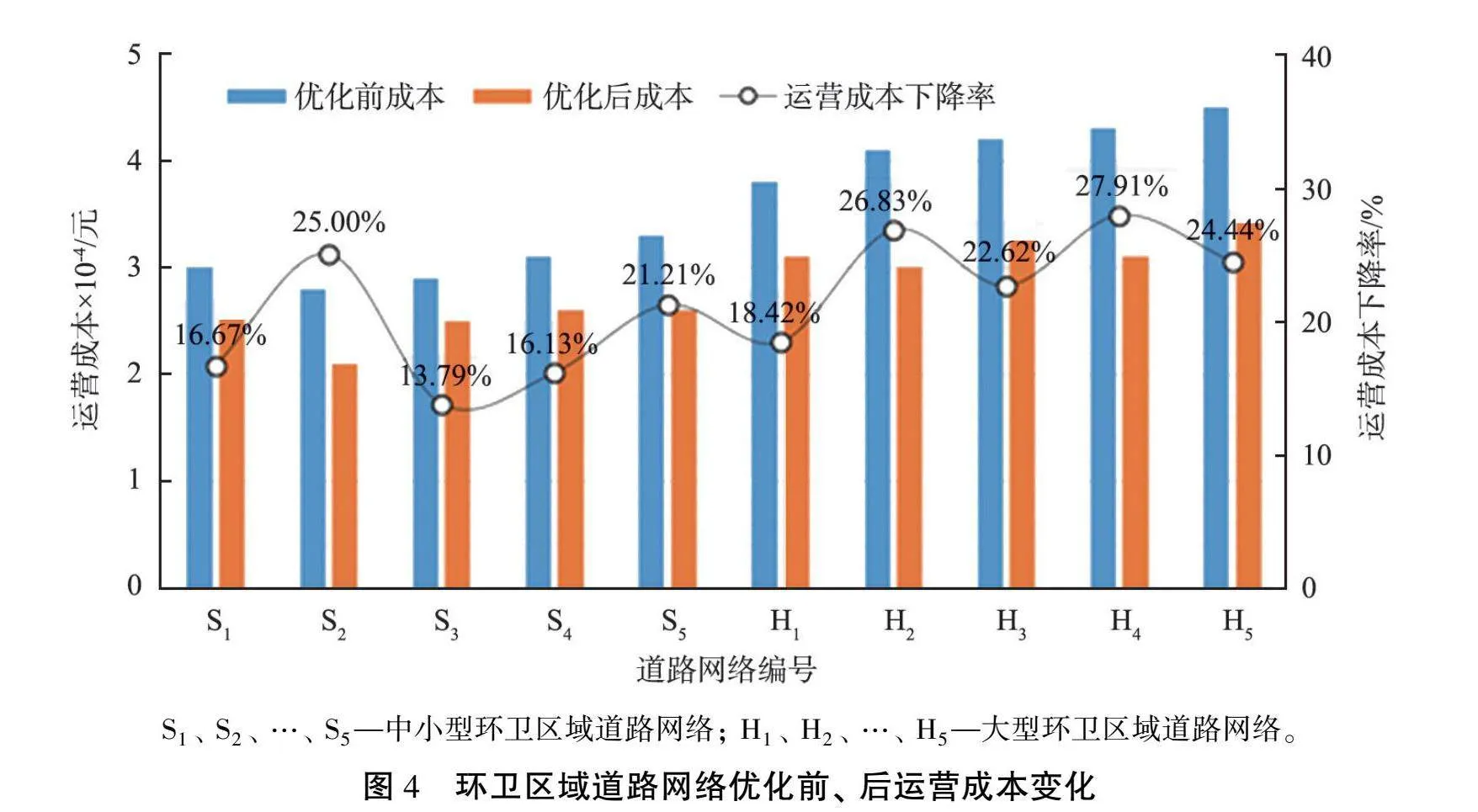
1）运营成本。 假设每辆环卫车的采购价格为105元， 平均行驶费用为15.4元/km。 图4所示为环卫区域道路网络优化前、后运营成本变化。 由图

可知： 所提出的系统优化方案应用于各环卫区域道路网络后， 运营成本均大幅降低。 中小型环卫区域道路网络优化后的运营成本显著下降， 降低约2.8×104元， 特别是S2、 S5， 运营成本下降率分别为25.00%、 21.21%； 大型环卫区域道路网络优化后总运营成本下降约5.05×104元， 其中H2、 H4下降幅度最大， 运营成本下降率分别为26.83%、 27.91%。 由此可知， 所提出的系统优化方案能大幅节约运营成本， 经济效益显著。

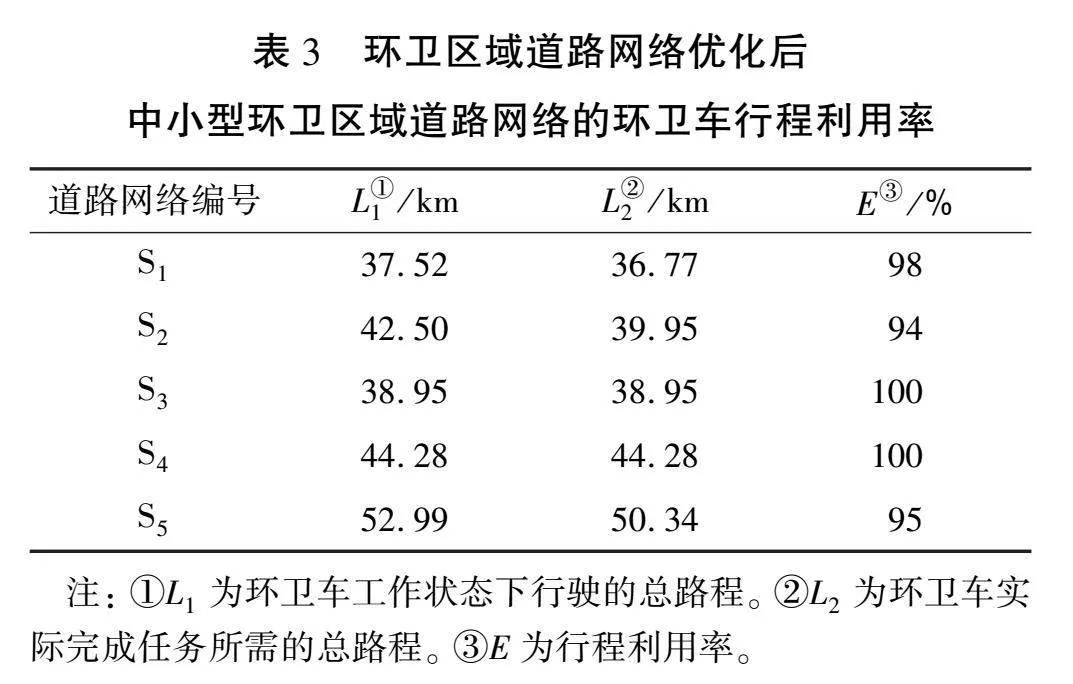
2）行程利用率。根据式（17），行程利用率E越大，则环卫车在非工作状态下行驶的距离越小，工作效率越高。本文中环卫车辆均安装环卫车智能控制器，其中采集模块可统计环卫车行驶总路程L2与工作状态下的行驶路程L1。表3所示为环卫区域道路网络优化后中小型环卫区域道路网络的环卫车行程利用率。由表可知： 对于中小型环卫区域道路网络，优化后环卫车平均行程利用率高达97.4%。5个中小型环卫区域道路网络的环卫车行程利用率都达到94%及以上，尤其是S3、 S4，甚至达到100%。由此可知，所提出的系统优化方案成功地提高了环卫车辆的行程利用率，从而使环卫区域道路网络的运行更高效和节约成本。

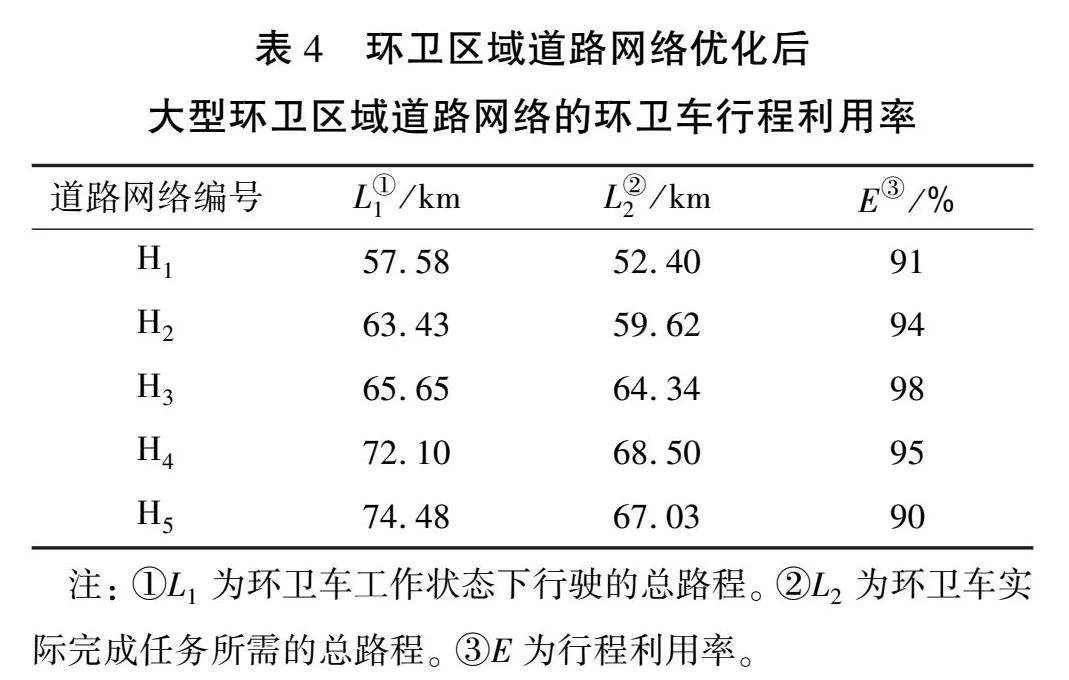
表4所示为环卫区域道路网络优化后大型环卫区域道路网络的环卫车行程利用率。 由表可知， 对于大型环卫区域道路网络， 平均行程利用率达到93.6%， 尤其是H3，行程利用率高达98%。 当环卫区域道路网络的规模越来越大时， 单个环卫区域道路网络的行程利用率有所降低， 但是平均行程利用率仍然不低于90%， 表明所提出的系统优化方案在不同规模环卫区域道路网络上均表现出良好的适用性。

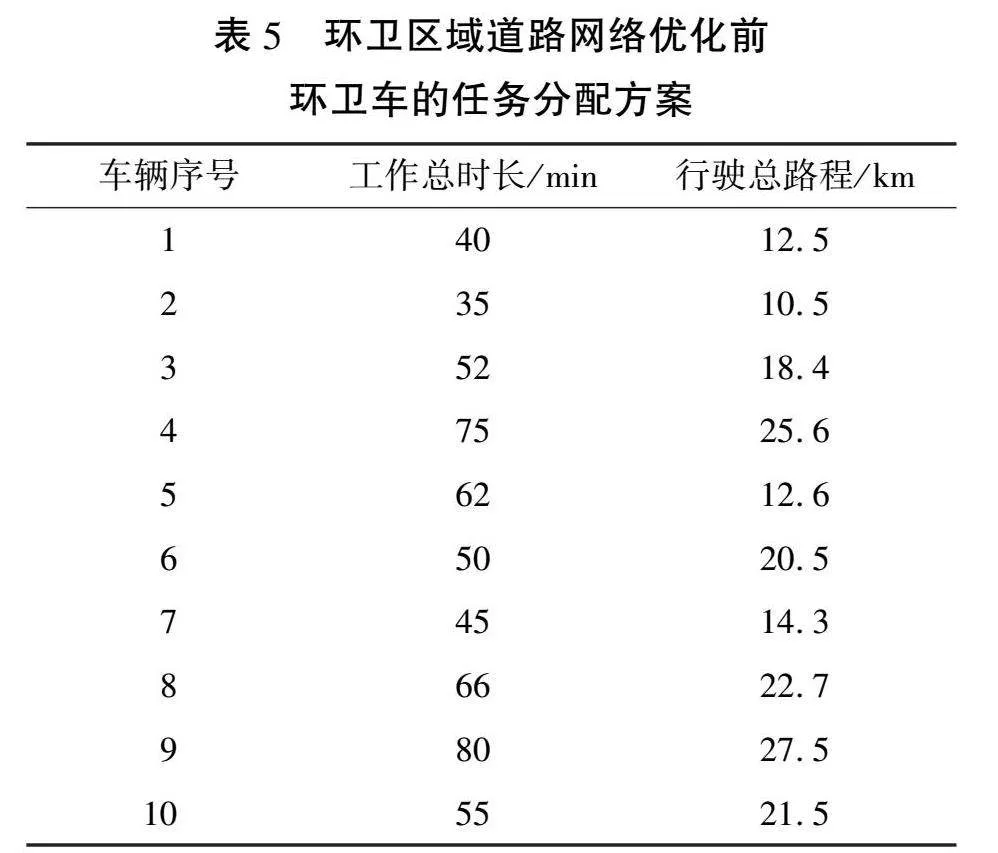
3）任务分配优化程度。以S1为例，表5所示为分配任务时不考虑任务分配优化程度，即不对环卫车添加任务量约束时，环卫车的任务分配方案。由表可知，在不考虑任务量约束的情况下，环卫车的任务分配优化程度为53.55%，任务量差异较大。

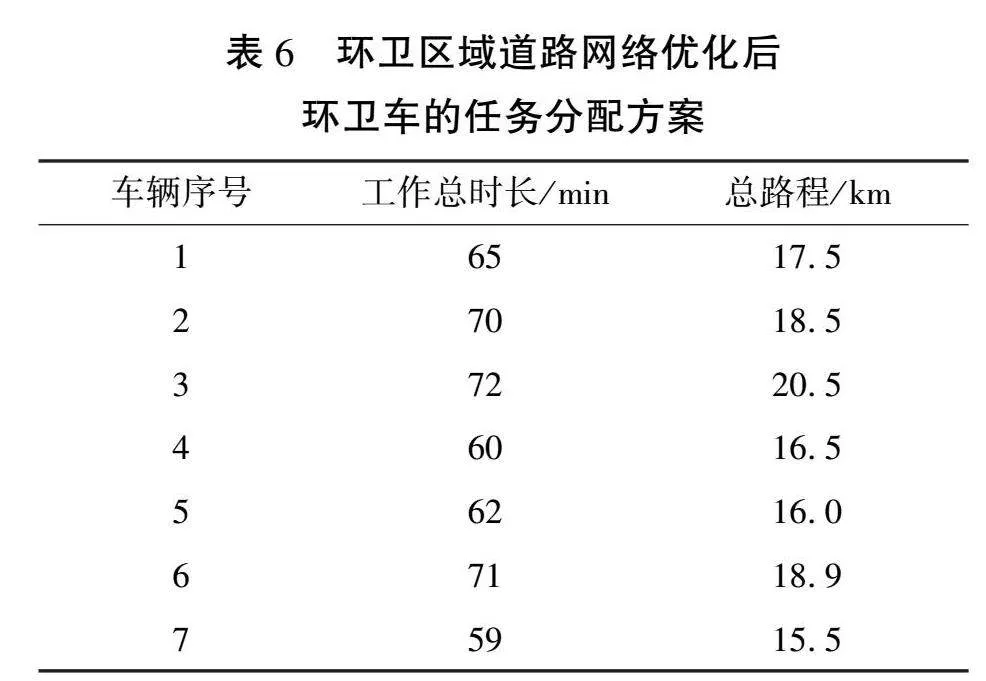
通过所提出的系统优化方案考虑任务分配优化程度，即添加任务量约束时，环卫车的任务分配方案如表6所示。由表可知，采用所提出的系统优化方案调整环卫车任务分配，完成相同的工作任务只需7辆环卫车，相较优化前的任务分配方案，减少使用3辆环卫车，有效降低了运营成本。由式（13）计算可得，任务分配优化程度提高到85.16%，任务均衡性大幅提升。

4 结论

本文中基于所构建的城市环卫车垃圾收运调度系统数学模型，提出城市环卫车垃圾收运调度系统优化方案，通过节约算法求出满足环卫车续航路程约束的最佳子路径，将这些子路径任务合理分配给环卫车，并利用研究区域内的环卫数据综合评估所提出的系统优化方案，得到以下主要结论：

1）与以顺序优先原则调度分配的优化前方案相比， 对于中小型环卫区域道路网络， 所提出的系统优化方案所需车辆数减少39.03%， 环卫运营成本下降约2.8×104元， 平均行程利用率达到97.4%； 对于大型环卫区域道路网络， 所提出的系统优化方案所需环卫车辆数减少18.78%， 总运营成本降低约5.05×104元， 平均行程利用率达到93.6%； 在有效提高作业效率的同时， 降低了环卫经济成本。

2）在同等任务量时，利用所提出的系统优化方案分配任务，配置环卫车减少3辆，任务分配优化程度提高到85.16%，在降低环卫运营成本的同时，有效地提高了工作效率，并且缩小了每辆环卫车之间的任务量差异。

参考文献：

［1］ 柴获， 何瑞春， 苏江省， 等. 求解双目标带时间窗车辆路径问题的蚁群算法［J］. 交通运输系统工程与信息， 2018， 18（4）： 156.

［2］ WUHL，TANFM，QIAO Q Q， et al. A chance-constrained vehicle routing problem for wet waste collection and transportation considering carbon emissions［J］. International Journal of Environmental Research and Public Health， 2020， 17（2）： 458.

［3］ TIRKOLAEEEB，GOLIA，PAHLEVAN M， et al. A robust bi-objective multi-trip periodic capacitated arc routing problem for urban waste collection using a multi-objective invasive weed optimization［J］. Waste Management amp; Research， 2019， 37（11）： 1089.

［4］ JIAN" G， QIANG M B， HAI W C. Feeder vessel routing and transshipment coordination at a congested hub port［J］. Transportation Research： Part

B Methodological， 202 151： 1.

［5］ 陈彦， 胡晓军， 卢川， 等. 基于混合整数规划模型的垃圾收运线路优化［J］. 交通科技与经济， 2019， 21（1）： 28.

［6］ 边展， 徐奇， 靳志宏. 带时间窗的甩挂运输路径优化问题研究［J］. 交通运输系统工程与信息， 2018， 18（2）： 183.

［7］ WILLEMSE E J， JOUBERT J W. Efficient local search strategies for the mixed capacitated arc routing problems under time restrictionswithintermediatefacilities［J］.Computersamp;Operations Research， 2019， 105： 203.

［8］ 陈梅， 李炳辉， 潘旺洋. 城市环卫车调度系统建模与路径规划研究［J］. 控制工程， 2019，26（9）：1751.

［9］ DOYURAN T， "ATAY B. A robust enhancement to the Clarke-Wright savings algorithm［J］. Journal of the Operational Research Society， 201 62（1）： 223.

［10］ 李军. 有时间窗的车辆路线安排问题的启发式算法［J］. 系统工程， 1996（5）： 45.

［11］ 衡红军， 晏晓东. 实现多目标优化的机场特种车辆调度算法［J］. 计算机应用与软件， 2016， 33（10）： 239.

［12］ 聂庆慧， 龙秀江， 梁程， 等. 多约束条件下城市道路环卫车优化配置与路径规划［J］. 交通运输系统工程与信息， 2022， 22（5）： 273.

（责任编辑：王 耘）