基于改进蜣螂优化算法优化BP神经网络

摘要：文章提出了一种利用改进蜣螂优化（IDBO）算法优化BP神经网络的新方法，通过Chebyshev混沌映射初始化种群，结合黄金正弦策略及动态权重系数实现高效搜索。基于MATLAB R2024a进行仿真，结果表明IDBO-BP模型在训练集和测试集上均表现优异，显著提升拟合度、泛化能力和预测精度，且收敛速度更快。此方法有效提升了神经网络性能，为解决复杂数据处理问题提供了新途径，展现了广阔应用前景。

关键词：BP神经网络；蜣螂优化算法；黄金正弦策略；Chebyshev混沌映射

中图分类号：TP3-05" 文献标志码：A

基金项目：大同市科技计划项目；项目编号：202305。2022年山西省高等学校教学改革创新项目；项目编号：J20220888。山西省教育科学“十四五”规划；项目编号：GH-220403。

作者简介：曹同宇（1995— ），男，硕士研究生；研究方向：地下空间技术。

0" 引言

随着近年来科技的不断进步，现代社会面临越来越复杂的工程问题。在当今复杂多变的数据处理领域，反向传播（Back Propagation，BP）神经网络凭借其强大的非线性映射能力和自学习能力，已成为处理分类、回归等任务的重要工具。然而，BP神经网络在训练过程中易陷入局部最优解，且存在收敛速度较慢的问题，这一直限制了其在实际应用中的效果。为了解决这些问题，研究者们不断探索新的优化算法。近年来，受蜣螂生物习性的启发，Xue等［1］提出了一种新型群智能优化算法——蜣螂优化（Dung Beetle Optimization，DBO）算法。该算法模拟了蜣螂的滚球、跳舞、觅食等行为，展现出强大的全局搜索能力和快速的收敛速度。因此，本文提出将DBO算法应用于BP神经网络的训练过程中，旨在通过DBO算法优化BP神经网络的权重和阈值，以期提高神经网络的性能，为解决复杂的数据处理问题提供新的思路和方法。DBO算法以其卓越的收敛速度和出色的稳定性在众多优化算法中脱颖而出［2-5］。与粒子群优化（Particle Swarm Optimization，PSO）算法［6］、鲸鱼优化算法（Whale Optimization Algorithm，WOA）［7］和哈里斯鹰优化（Harris Hawks Optimization，HHO）算法相比［8］，DBO算法凭借其独特的蜣螂集群行为模拟机制，能够迅速且稳定地逼近全局最优解。无论是处理连续、离散还是多模态等复杂优化问题，DBO均展现了其强大的适应性。

1" 理论基础

1.1" BP神经网络

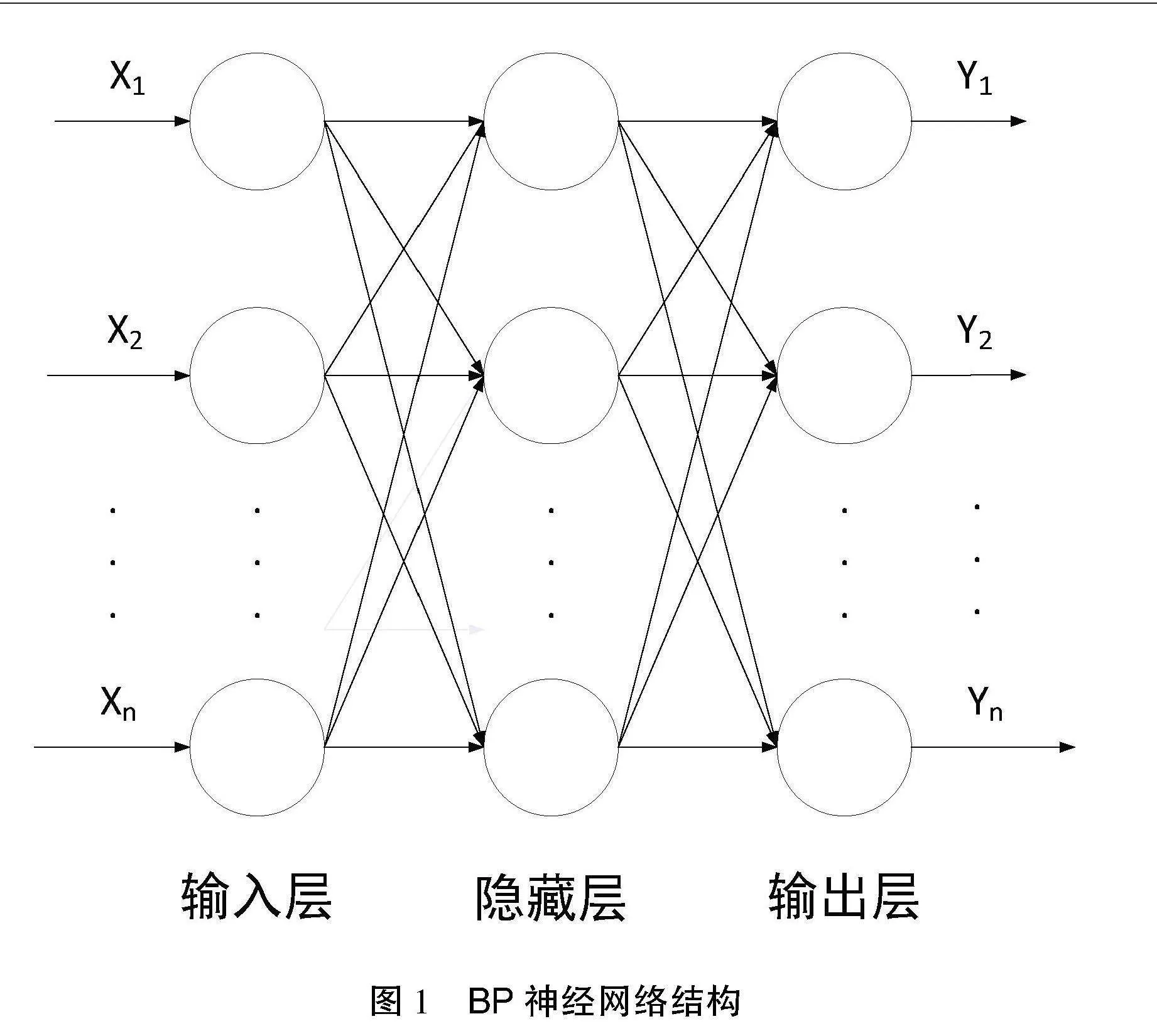
BP神经网络，全称为反向传播神经网络，是由Rumenlhart团队提出的一种基于误差反向传播算法的人工神经网络模型［9-10］。其通过模拟生物神经网络的结构和功能，实现了对输入数据的非线性映射和分类。BP神经网络由输入层、隐藏层和输出层组成，如图1所示。通过前向传播计算输出结果并利用反向传播算法根据输出结果与实际标签之间的误差调整网络权重和偏置，以优化网络性能。BP神经网络采用梯度下降法来更新权重，因此在训练过程中可能会陷入局部最优解。若使用该算法去解决实际问题，则须要对BP神经网络进行进一步的优化［11］。

1.2" 蜣螂优化算法

蜣螂优化算法是一种新型的群体智能优化算法。该算法受到自然界中蜣螂的生存行为启发，通过模拟蜣螂行为来寻找优化问题的最优解。

1.2.1" 滚球行为

蜣螂在无障碍物的情况下，利用太阳导航使粪球沿直线滚动。该过程的公式为：

Xi（t+1）=xi（t）+a×k×xi（t-1）+b×Δx（1）

Δx=|xi（t）-Xw|（2）

其中，t为当前迭代次数，xi（t）表示第i只蜣螂在第t次迭代时的位置信息，α为自然系数（取-1或1），k∈（0，0.2］为偏转系数，Xw表示为全局最差位置，b∈（0，1）为常数。|xi（t）-Xw|表示光线强度，其值越高，则光线强度越弱。

1.2.2" 跳舞行为

当蜣螂遇到障碍物无法前进时，可变换方向获得新的移动路线。该过程的公式为：

Xi（t+1）=xi（t）+tan（θ）×|xi（t）-xi（t-1）|（3）

其中，θ为偏转角，在区间［0，π］内取值。当θ为0、π/2、π时，蜣螂的位置不更新。|xi（t）-xi（t-1）|代表第i只蟑螂在第t次与t-1次的位置偏移量。

1.2.3" 繁殖行为

研究采用边界选择策略模拟雌性蜣螂的产卵区域，动态调整产卵区。该过程的公式（产卵区选择）为：

L*b=max（X*×（1-R），Lb）（4）

U*b=min（X*×（1+R），Ub）（5）

其中，X*为当前局部最优位置，L*b和U*b分别为产卵区的下限和上限，R=1-tTmax，Tmax为最大迭代次数，Lb和Ub分别为优化问题的下限和上限。

成熟的蜣螂从地下钻出寻找食物，觅食区域动态更新。该过程的公式（觅食区选择）为：

Lbb=max（Xb×（1-R），Lb）（6）

Ubb=min（Xb×（1+R），Ub）（7）

其中，Xb为全局最优位置，Lbb和Ubb分别为最佳觅食区域的下限和上限。小蜣螂的位置更新公式为：

xi（t+1）=xi（t）+C1×（xi（t）-Lbb）+C2×（xi（t）-Ubb）（8）

其中，C1为遵循正态分布的随机数，C2∈（0，1）为随机向量。

1.2.4" 偷窃行为

偷窃作为一种竞争行为，在蜣螂种群中常见。该过程的公式为：

xi（t+1）=Xb+S×g×{|xi（t）-X*|+|xi（t）-Xb|}（9）

其中，Xb为食物竞争的最佳位置，xi（t）为第i只小蜣螂在第t次迭代的位置信息，g为一个遵循正态分布的大小为1×D的随机向量，S表示一个常数值。

1.3" 基于改进蜣螂优化算法的BP神经网络优化方法

由于BP神经网络生成时，初始权值和阈值一般为随机初始化。这会导致训练稳定性和收敛速度下降，神经网络需要经过多次迭代和调整才能找到合适的权值和阈值，并且伴随陷入局部最小值的风险。为解决这个问题，采用IDBO算法优化BP神经网络的初始权值和阈值。BP神经网络的权值和阈值作为IDBO算法中蜣螂的位置信息。然后，使用训练数据来评估BP神经网络的性能（如预测误差），并将该性能作为蜣螂的适应度值。采用IDBO算法优化BP神经网络的流程如图2所示。

2" 改进蜣螂优化算法

2.1" Chebyshev混沌映射

Chebyshev混沌映射是一种基于Chebyshev多项式的混沌映射方法［12］，通常在数值分析和逼近论中使用，具有良好的伪随机特性以及对初始参数敏感的特性。相较于常见的集中离散混沌映射［13］，Chebyshev混沌映射更具优势。本文选取Chebyshev混沌映射对DBO进行种群初始化生成混沌变量，如式（10）所示。

xn+1=cos（k×arcosxn），xn［-1，1］（10）

Chebyshev混沌映射蜣螂优化算法步骤如下。

规定蜣螂种群数量为i，网络节点个数为d，生成式（11）所示矩阵。

X=X1，1" X1，2" …" X1，d

X2，1" X2，2" …" X2，d

" """

Xi，1" Xi，2" …" Xi，d

（11）

利用Chebyshev混沌映射对矩阵迭代初始化，将混沌值映射到指定的上下界，如式（12）所示。

Xid=|Xid×（Ub-Lb）+Lb|（12）

其中，Ub、Lb分别优化参数的目标上限与下限，Xid为第i只蜣螂第d维，Xid为第i只蜣螂在搜索空间中第d维坐标值。

2.2" 黄金正弦策略

黄金正弦策略是一种由Tanylidizi等［14］于2017年提出的新型元启发式优化算法。该算法的设计源于数学中的正弦函数，并结合黄金分割比例来提高搜索效率和优化能力。

初始化：在算法的初始阶段，随机生成一个包含s个个体的种群。每个个体在d维解空间中都有一个位置，用Xti=（Xi1，Xi2，…，Xid）表示第t次迭代中第i个个体的位置。此外，为每个个体维护一个最优位置Pti=（Pi1，Pi2，…，Pid），用于记录该个体到目前为止找到的最佳解。随着迭代的进行，不断更新这些位置和最优位置，直到满足算法的终止条件。

位置更新公式如下：

Xti=Xti×|sin（R1）|+R2×sin（R1）×|x1×Pti-x2×Xti|（13）

x1=-π+（1-τ）×2π（14）

x2=-π+τ×2π（15）

其中，R1［0，2π］为下次迭代随机移动的距离，R2［0，π］为下次迭代移动的方向。引入黄金正弦策略进行每一次迭代后，蜣螂个体都会与最优个体进行交流，利用最优解信息解决原算法中的个体缺乏交流的情况。黄金正弦策略扩大了搜索空间，对原算法陷入局部最优解的问题进行了优化，提升了算法寻求最优解的能力。

2.3" 位置更新动态权重系数

为避免陷入局部最优解，本文引入位置更新动态权重系数的公式如下：

Xti=k1×Bx+k2×（|Rti-Bxx|+|Rti-Bx|）

k1=1-t3T3

k2=t3T3（16）

其中，t为当前迭代次数，T为最大迭代次数，Bx为当前最优解，Bxx为全局最优解，Rti为当前迭代次数第i个蜣螂位置的信息。在迭代优化过程中，权重系数k1初期较大，随着迭代进行，权重系数k2逐渐增大，引导蜣螂在已发现的最优区域附近进行深入开发，以实现全局搜索与局部开发的平衡。

3" 仿真实验

3.1" 仿真实验环境搭建和实验参数设置

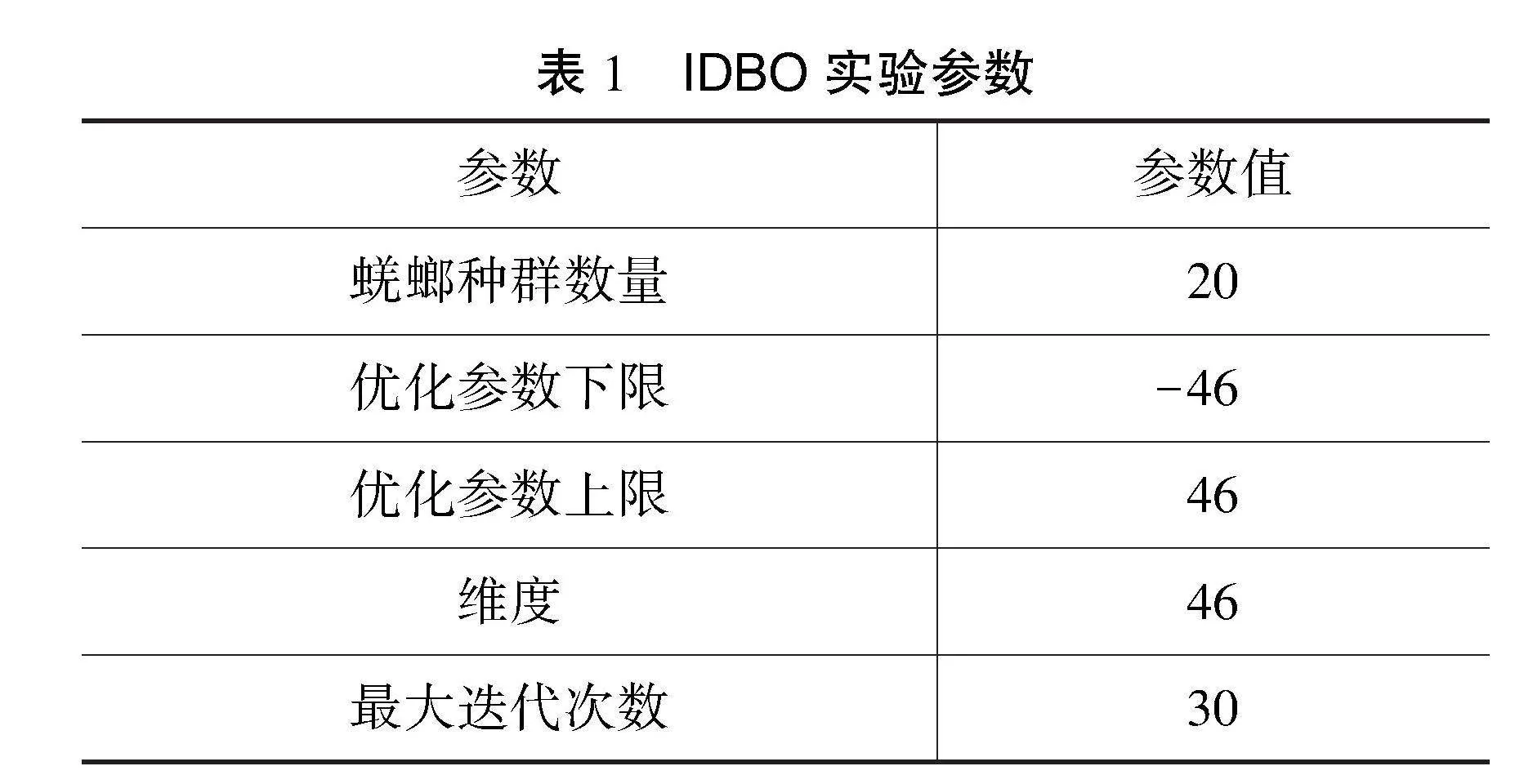
为了保证实验的准确性和严谨性，本文基于Mircosoft windows 11、CPU硬件配置为3th Gen Intel（R） Core（TM） i9-13900HX 2.20 GHz、32 GB内存的仿真平台进行实验。代码程序在MATLAB R2024a上实现。IDBO参数设置如表1所示。

3.2" 结果分析

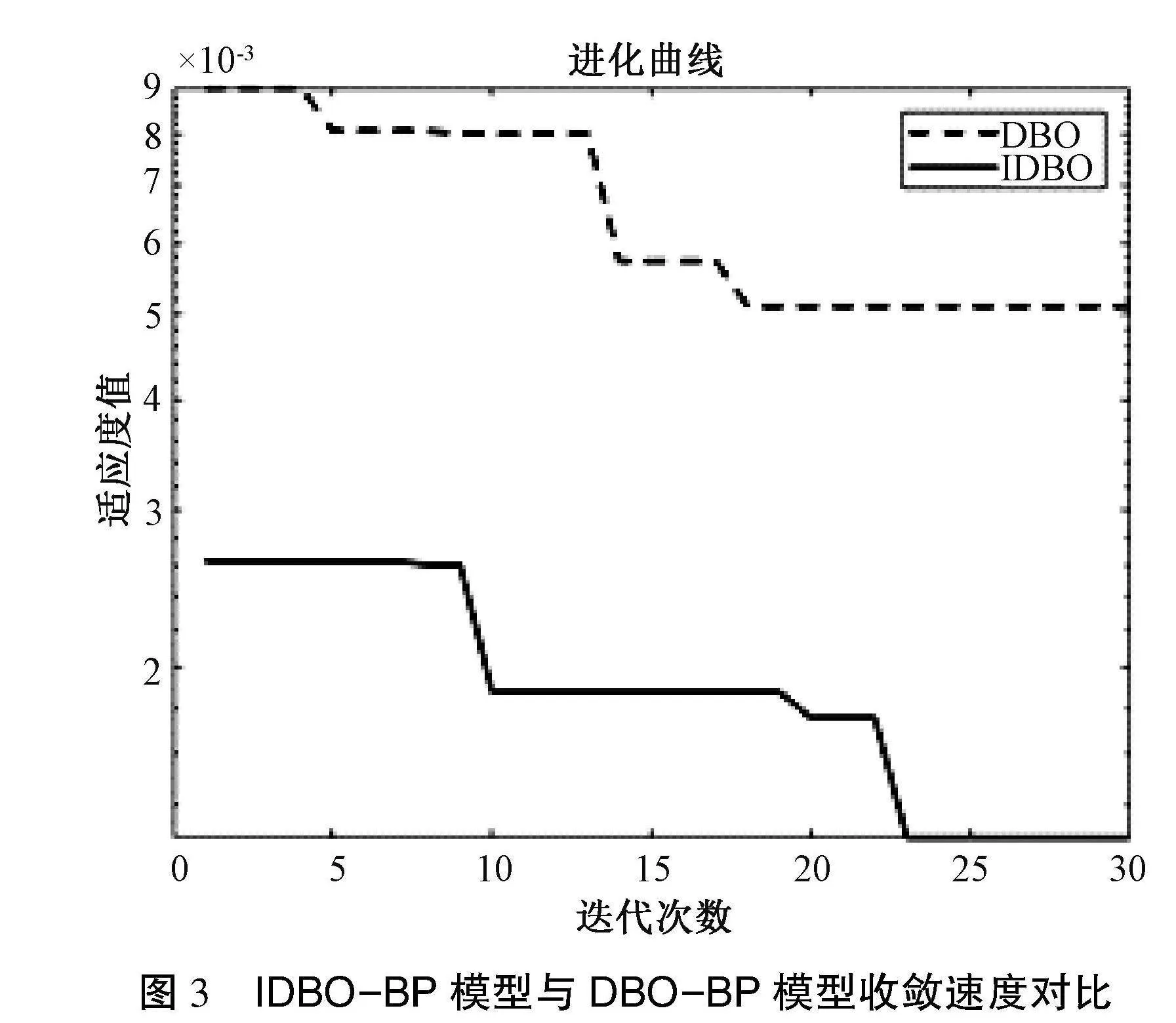
为了验证IDBO-BP模型预测的准确性，本文实验采用随机生成的数据集，并将其在IDBO-BP模型和DBO-BP模型中进行比较。IDBO-BP与DBO-BP的收敛性如图3所示。

随着迭代次数的增加，模型的适应度不断下降，适应度值越小说明越接近问题的最优解。相较于DBO-BP，IDBO-BP的初始适应度值更小，适应度下降速率更快，这说明IDBO-BP算法能更快地接近最优解。

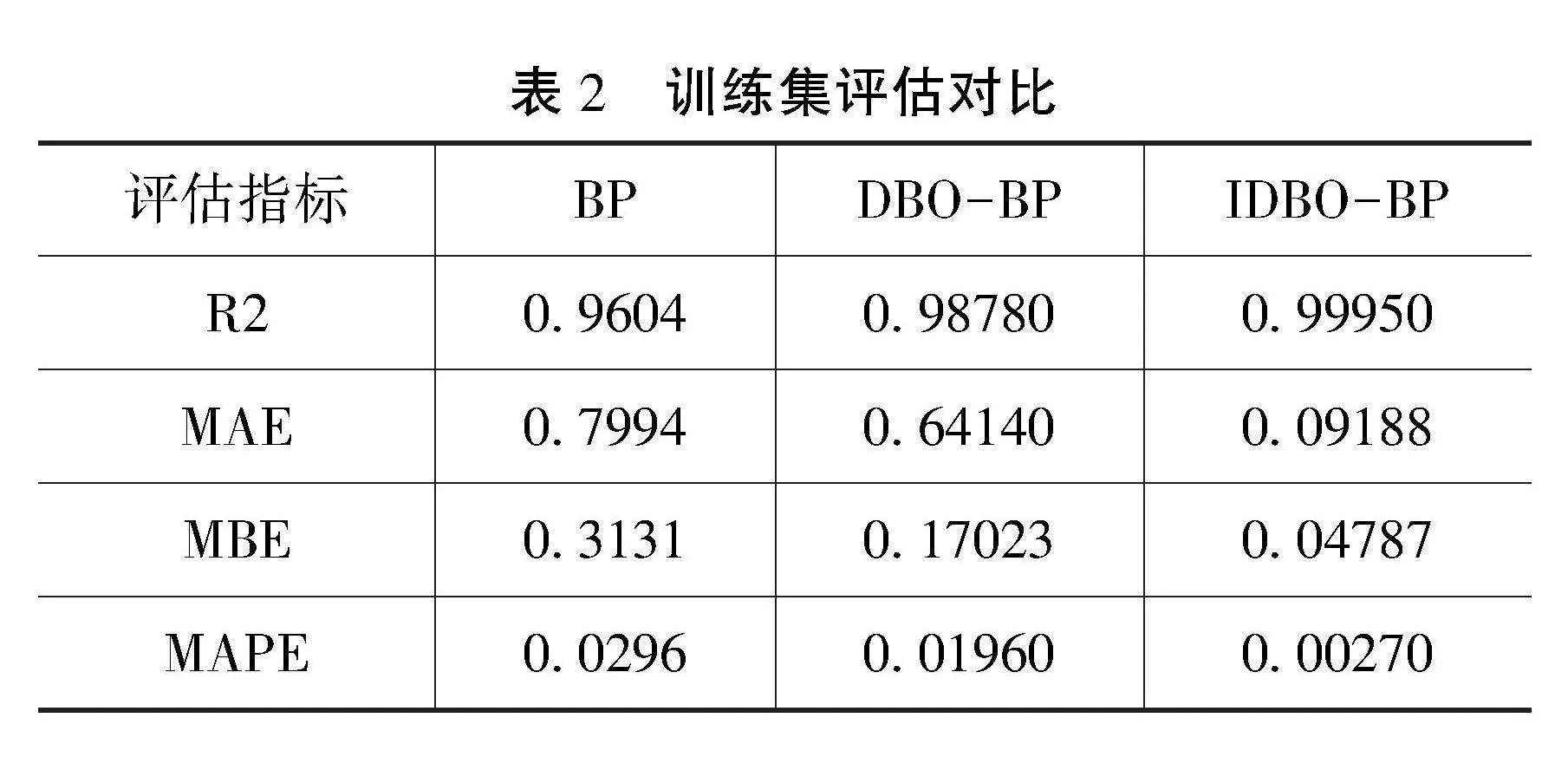
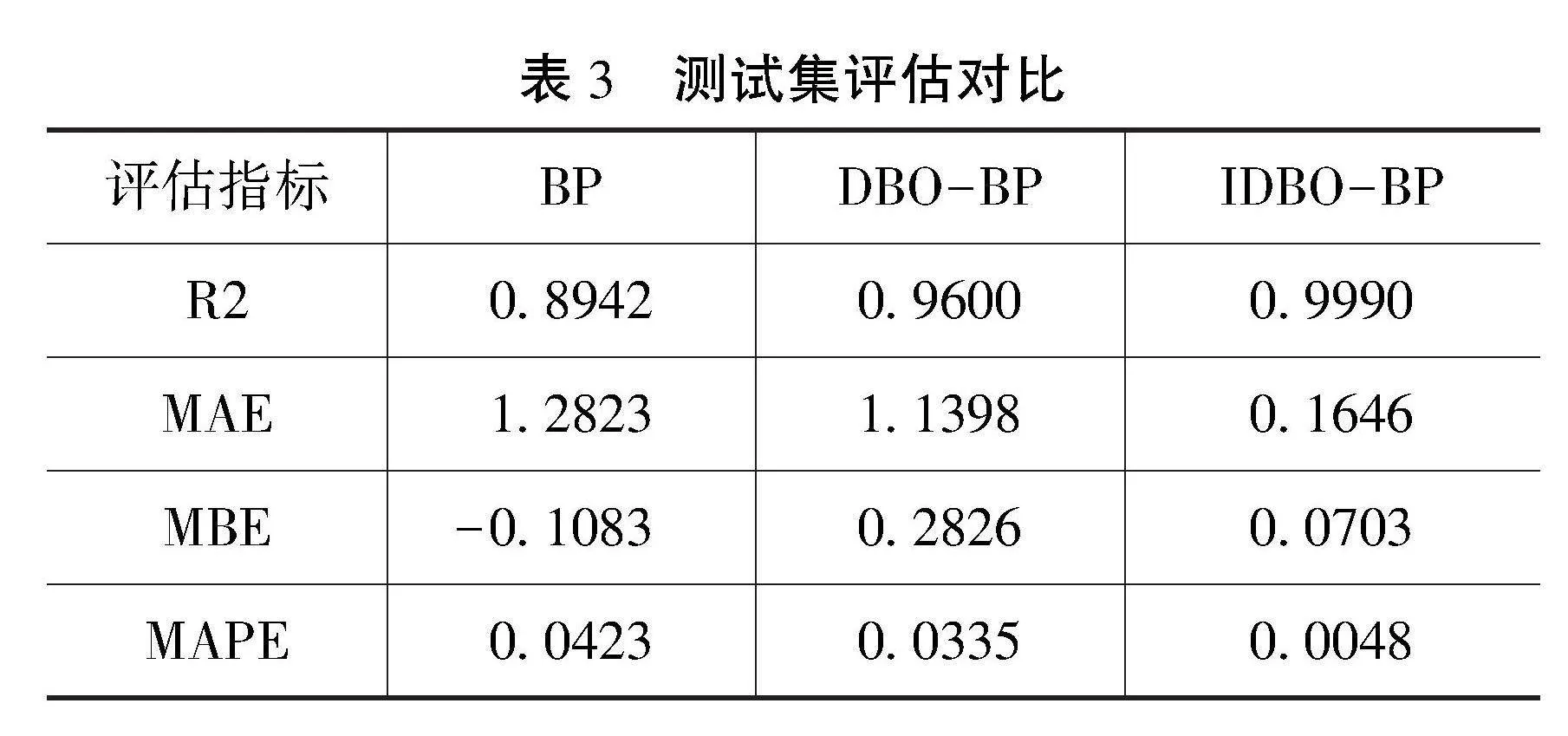
如表2—3所示，本文比较了3种不同的神经网络模型（BP、DBO-BP、IDBO-BP）在训练集和测试集上的性能，使用4种不同的评估指标：R2（决定系数）、平均绝对误差（Mean Absolute Error，MAE）、平均偏差误差（Mean Bias Error，MBE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）。

下面是对这些数据的详细分析：IDBO-BP模型在评估中表现卓越，其训练集与测试集的R2值均接近1，MAE最低，MBE接近0，且MAPE显著优于BP和DBO-BP模型。这些指标共同表明IDBO-BP不仅拟合度高，还具备强大的泛化能力和高精度的预测性能，在三者中最优。

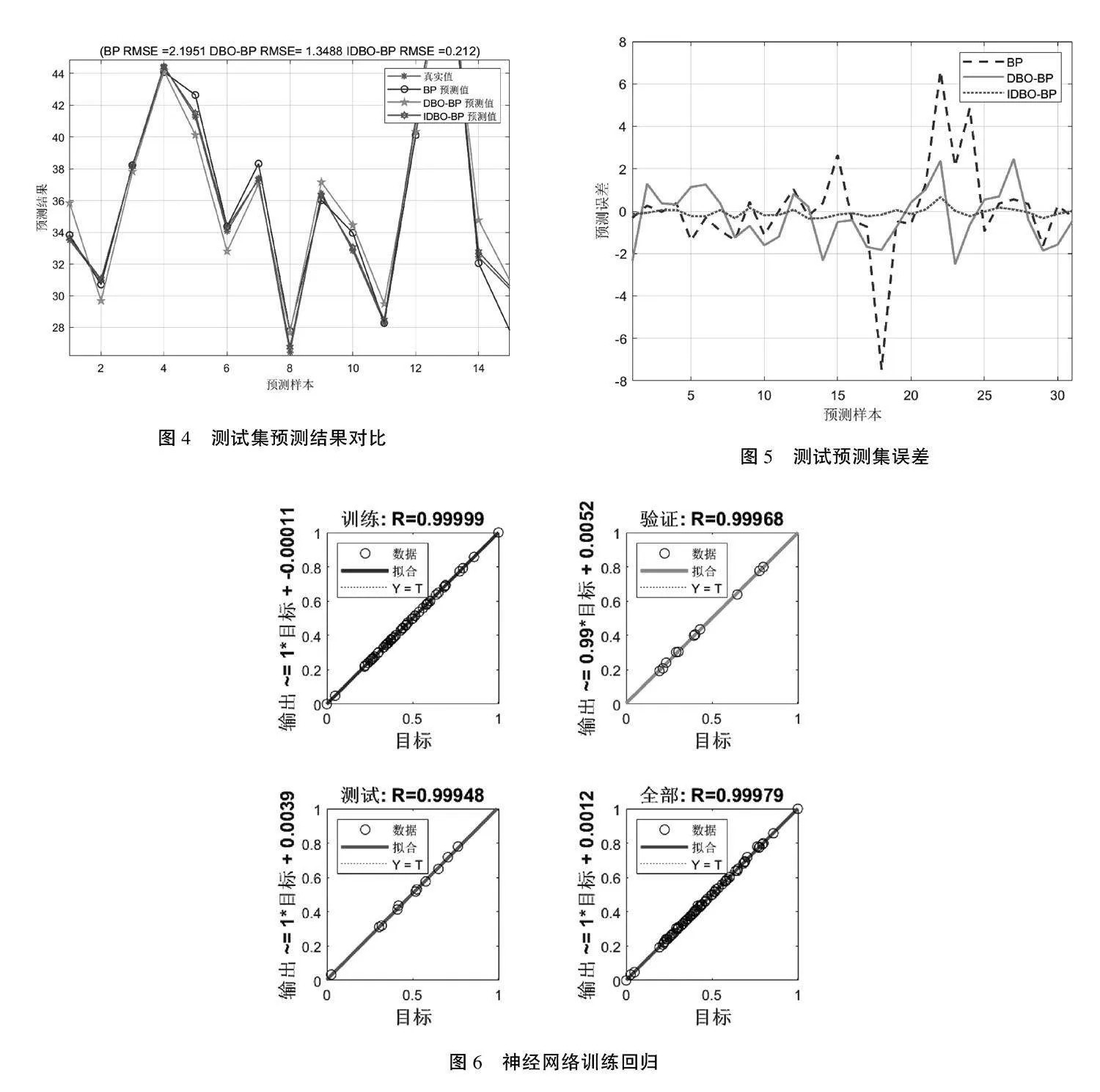
BP、DBO-BP、IDBO-BP测试集预测结果如图4所示。从图中可以明显看出，IDBO-BP模型的预测值更加接近真实值。对比3种模型测试集的均方根误差（Root Mean Square Error，RMSE）可以看出，IDBO-BP模型的RMSE小于BP、DBO-BP模型，这说明其在测试集上的预测误差更低，预测更加准确。

3种模型的测试预测集误差曲线如图5所示。由图可知：IDBO-BP模型的预测误差是三者中最低的。预测误差越低，则模型能更好地捕捉数据中的规律并作出更精确的预测。这表明IDBO-BP模型在预测未知或测试数据时的准确性更高。

神经网络训练回归曲线如图6所示。由图可知：IDBO-BP模型在训练集、验证集和测试集上的R2值均极高，分别为0.99999、0.99968和0.9948，这表明" 其拟合度卓越且泛化能力强，整体R2为0.99979，显示了模型高准确性和可靠性。

4" 结语

本文提出并验证了IDBO优化BP神经网络的新方法，通过Chebyshev混沌映射初始化、黄金正弦策略更新位置及动态权重系数，解决了BP网络易陷局部最优和收敛慢的问题。实验结果显示，IDBO-BP模" 型在训练与测试集上的表现均优于传统BP模型及DBO-BP模型，具备更快的收敛速度和全局搜索能力。其预测准确性高、误差低，为复杂数据处理提供了新思路与有效手段。

参考文献

［1］XUE J，SHEN B. Dung beetle optimizer：a new meta-heuristic algorithm for global optimization［J］. The Journal of Supercomputering，2023（7）：7305-7336.

［2］王莲霞，李丽敏，任瑞斌，等.基于STM32和DBO-BP的滑坡预警系统［J］.国外电子测量技术，2023（8）：139-146.

［3］ZHANG R Z，ZHU Y J. Predicting the mechanical properties of heat-treated woods using optimization-algorithm-based BPNN［J］. EI，2023（5）：1-35.

［4］WU C L，FU J C，HUANG X R，et al. Lithium-ion battery health state prediction based on VMD and DBO-SVR［J］. EI，2023（10）：1-27.

［5］周亚中，何怡刚，邢致恺，等.基于IDBO-ARIMA的电力变压器振动信号预测［J］.电子测量与仪器学报，2023（8）：11-20.

［6］LI B，TIAN X T，ZHANG M. Thermal error modeling of machine tool spindle based on the improved algorithm optimized BP neural network［J］. The international Journal of Advanced Manufacturing Technology，2019（9）：1497-1505.

［7］丁艺鼎，蒋名亮，徐力刚，等.基于鲸鱼优化算法的长短期记忆模型水库洪水预报［J］.湖泊科学，2024（1）：320-332.

［8］李天翔，李江，卢亚峰.基于HHO-LSSVM的露天煤矿抛掷爆破效果预测研究［J］.中国安全生产科学技术，2023（增刊1）：110-116.

［9］RUMELHART D E，HINTON G E，WILLIAMS R J. Learning representations by back-propagating errors［J］. Nature，1986（6088）：533-536.

［10］RUMLHART D E，MCCLELLAND J L，CORPORATE PDP Research Group. Parallel distributed processing：explorations in the microstructure of congnition，volume 1：foundations［M］. Cambridge：MIT Press，1986.

［11］焦李成，杨淑媛，刘芳，等.神经网络七十年：回顾与展望［J］.计算机学报，2016（8）：1697-1716.

［12］CHATTERJEE S，ROY S，DAS A K，et al. Secure biometric-based authentication scheme using Chebyshev chaotic map for multi-server environment［J］. IEEE Transactions on Dependable and Secure Computing，2016（5）：824-839.

［13］隗小斐，何如龙，陈津.基于混沌加密的水声扩频通信技术［J］.舰船科学技术，2022（5）：101-104.

［14］TANYLIDIZI E，DEMIR G. Golden sine algorithm：a novel math-inspired algorithm［J］. Advances in Electrical and Computer Engineering，2017（2）：71-78.

（编辑" 沈" 强）

Optimize BP neural network based on improved dung beetle optimization algorithm

CAO" Tongyu1， QIAO" Dong2， GUO" Ziyu1， ZHU" Shoujian1

（1.School of Coal Engineering，Shanxi Datong University， Datong 037009， China; 2.School of Architecture

and Surveying Engineering， Shanxi Datong University， Datong 037009， China）

Abstract： A new method of optimizing BP neural network by using improved dung beetle optimization（IDBO） algorithm is proposed in this paper. The population is initialized by Chebyshev chaotic map， and the efficient search is realized by combining golden sine strategy and dynamic weight coefficient. Based on the MATLAB R2024a， the simulative result shows that the IDBO-BP model performs well on both the training set and the testing set， which significantly improves the fitting degree， generalization ability and prediction accuracy， and the convergence speed is faster. This method effectively improves the performance of neural networks， provides a new way to solve the complex data processing problems， and shows a broad application prospect.

Key words： BP neural network; dung beetle optimization algorithm; golden sine strategy; Chebyshev chaotic map