基于无人机倾斜摄影测量矿区地形高程对比分析与应用

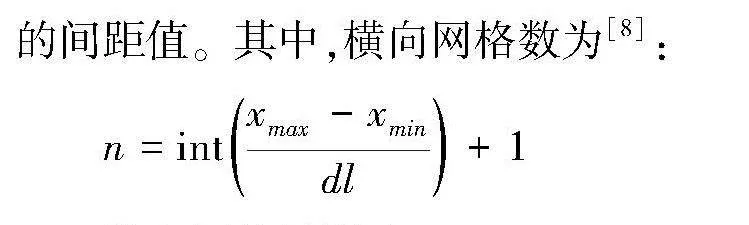
摘要：文章以山西省兴县奥家湾乡芦芽山东麓区域的峁底煤矿作为研究区域，进行无人机倾斜摄影测量的高程对比分析。文章对无人机图像进行三维建模，获取三维模型；生成高程数据，进行高程点匹配；对不同飞行高度下各区域进行高程对比分析，统计各区域参数，分析不同区域地形特征，高程变化特点；对高程数据求差，统计求差数据的参数，分析数据误差原因；选定分析区域，进行沉陷分析。

关键词：无人机倾斜摄影测量；三维模型；高程对比；沉陷分析

中图分类号：P228" 文献标志码：A

基金项目：江苏省研究生科研与实践创新计划项目；项目名称：基于无人机影像数据地形图等高线自动生成系统研制；项目编号：SJCX22_1250。

作者简介：王浩宇（1998— ），男，硕士研究生；研究方向：变形监测，开采沉陷分析。

0" 引言

无人机倾斜摄影测量技术是一项利用无人机搭载倾斜摄影系统的先进技术，通过航拍获取地表图像和数据。该技术充分发挥了无人机的灵活性和倾斜摄影的高精度特点，为地理信息系统（Geographic Information System，GIS）、测绘、建筑和土木工程等［1-3］领域图像信息难以获取的问题提供了创新性的解决方案。近年来，无人机倾斜摄影技术取得了显著进展。无人机成本的降低使得该技术更容易被广泛应用。同时，计算能力的提高使得无人机能够进行实时数据处理和分析，为用户提供及时的地理信息支持。然而，无人机采集的数据受多种因素的影响，包括飞行环境和传感器性能等，存在一定的噪声和误差。对来自不同时间的数据进行标定和配准也是一个复杂而重要的任务。确保数据的一致性和匹配性是无人机倾斜摄影测量数据处理中至关重要的问题。本文以山西省兴县奥家湾乡芦芽山东麓区域的峁底煤矿作为研究区域，进行无人机倾斜摄影测量的高程对比分析。

1" 无人机影像数据获取与处理

山西兴县华润联盛峁底煤业有限公司隶属于奥家湾乡管辖范围，位于中国山西省兴县县城东南方向5 km的峁底、王家崖村一带。该公司的地理坐标范围为东经111°09′47″至111°11′23″，北纬38°25′54″至38°27′39″。在该研究区域的西部与东部为山峰区域，中部地区为一条狭长的山谷，在山谷中有多块平原，有一条公路贯穿南北，在公路边有一条干涸的河床。在该研究区域的南部存在一片居民区，由于开采导致该区域存在许多裂缝与塌陷区域。综上所述，该研究区域地形地貌较为复杂，水资源较为匮乏，但交通较为便利。

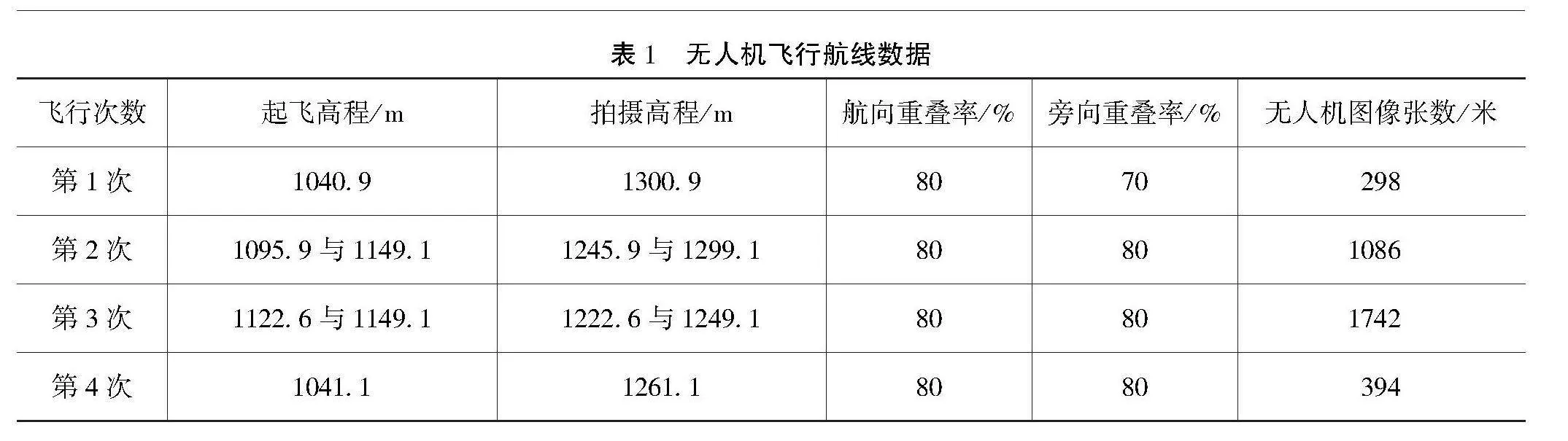
本次设计的4次不同飞行高度的航线均为井字形飞行无人机，井字型飞行是一种常用的飞行模式，其在航线规划中以井字形状进行飞行路径的设计和执行。本文设计了多条无人机飞行航线，以确保对研究区域的全面覆盖。该设计允许研究者获取不同飞行高度下的航拍影像，从而保证获得完整的地理信息和高程数据。这种多层次的数据采集能够确保足够的覆盖范围，为后续的三维建模工作提供支持［4］。然而，不同飞行高度无人机图像的三维建模精度有所差异，这就须要通过不同飞行数据来确保最为准确的三维模型数据。无人机飞行航线数据如表1所示。

本文设计该矿区进行的4次无人机飞行在2 d内完成，可获取海量的无人机倾斜摄影测量图像，飞行日光照情况良好，无人机倾斜摄影测量图像较为可靠，为后续的高程对比分析提供了数据基础。

无人机影像处理使用Context Capture软件，该软件可以对无人机飞行拍摄的彩色图片进行高效、精密的处理［5］。首先，本文将4次无人机影像分批次导入工程，Context Capture可以自动获取相机焦距以及传感器尺寸；其次，通过空中三角测量获取缺失的影像信息，通过平差调整获得最优数据；再次，可以通过重建项目对空间参考系统进行设置，通过规则平面网格的切块处理，获得相同大小的瓦片，提高三维重建的效率；最后，通过三维重建获得与切块个数相等的OSGB文件，本文采用Context Capture中的CC_S3Ccomposer OSGB模型解决坐标转换、数据对齐和匹配等问题，将多个单独的三维模型进行融合，以生成一个综合模型［6］。

在4次无人机三维模型生成后，为了更好地理解和分析数据，本文对该模型进行区域划分。在选择区域时，本文参考了无人机获取的高分辨率图像数据以及其他相关信息。通过分析图像数据中的地形特征，本文能够将模型中的区域划分为具有相似特征的部分。这种区域划分有助于研究者更好地理解模型中的不同地貌和景观特征，能够为后续的分析和应用提供更准确的基础。由于每次无人机飞行的区域边界存在差异，并且内部区域具有不同的特征和属性，因此本文选择2个山峰特征区域和2个平原特征区域进行分析。

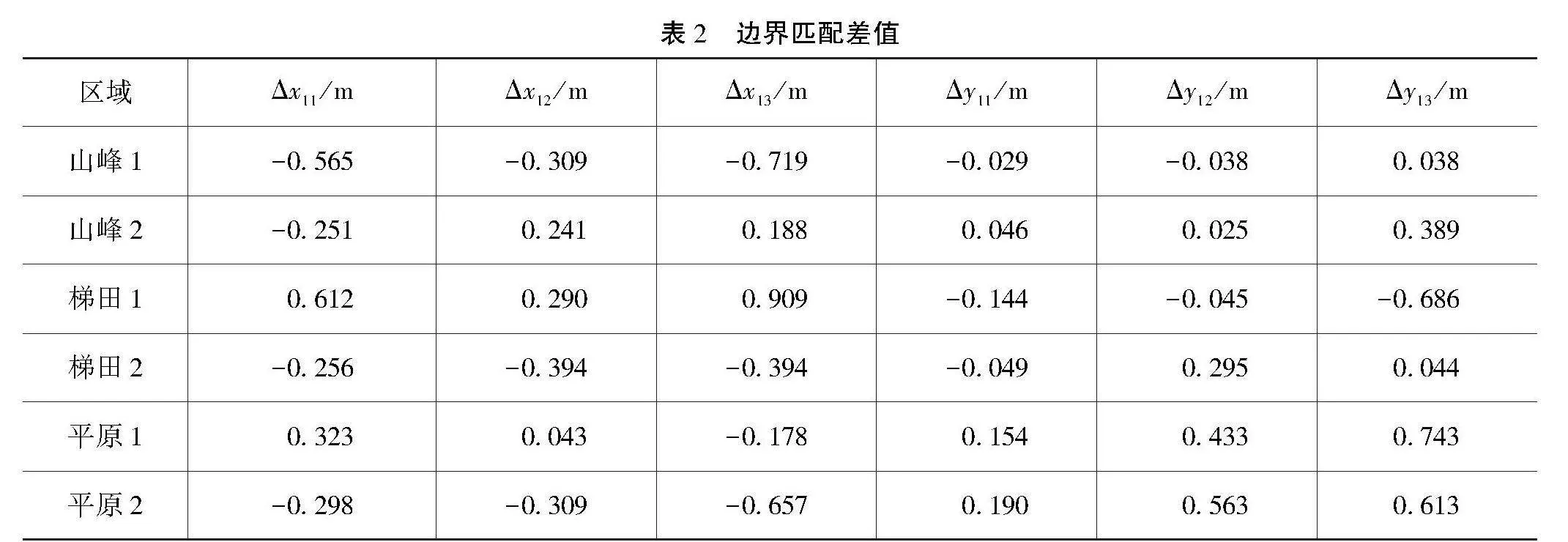
在各区域内相同区域内每间隔5 m生成一个高程点，研究者针对每个高程点的位置进行匹配操作。由于边界线与交界处高程点生成的数量可能存在不一致的情况，研究者须要删除多余点，以获得相应位置正确的高程点数据。以第一次飞行为基准，x、y各点的坐标差距如表2所示。

由表2可知，在不同飞行高度和不同区域下，相同特征点的坐标是不同的。然而，研究者发现内部生成的各点坐标差距与边界点的差距相同。因此，本文可以将这些差距相同的点认定为同一点，进行后续的高程误差分析。

通过进行误差分析和点的匹配，本文得到了不同区域中的高程点数量。对提取的高程点进行匹配，若在不同飞行高度获得的相同高程点的坐标x与y差值小于该研究区域的边界匹配的差值，则认定该高程点为同一点；否则，认定该高程点无效。

通过对高程点的匹配与验证，本文得到最终生成的各区域高程点。其中，山峰1区域有761个点，山峰2区域有875个点，梯田1区域有133个点，梯田2区域有592个点，平原1区域有657个点，平原2区域有1216个点。这些高程点的匹配将为后续的高程误差分析提供数据基础。

2" 不同无人机飞行高度高程对比分析

本文通过最大值、最小值和标准差对高程差值进行分析，获取不同飞行高度高程对比的分析结果。

标准差在高程数据中的意义在于提供了对地形变化或地貌特征的定量评估。标准差σ的公式如下［7］：

σ=∑ni=1hi-h-2n-1（1）

其中，hi为各个高程点，h-为平均值。通过计算高程数据的标准差，研究者可以了解地形起伏的强度、地表变化的幅度以及地貌特征的分布情况。较大的标准差通常表示地形或地貌的复杂性和多样性，而较小的标准差则表明地形或地貌相对均匀或单一。其可以帮助研究者识别地形的复杂性、评估地貌的多样性、分析地形变化的强度。

相关系数是用来衡量2组变量之间线性相关程度的统计量，其可以反映2组数据的变动趋势是否一致以及变化的方向。相关系数χ的公式如下［7］：

χ=∑ni=1xi-x-yi-y-∑ni=1xi-x-2∑ni=1yi-y-2（2）

其中，xi和yi为2组数据各点高程值，x-和y-为2组数据各自的平均值。相关系数的取值范围在-1到1之间，其中-1表示完全负相关，0表示无相关，1表示完全正相关。在2组高程数据中，相关系数用于衡量2组数据之间的关联程度。

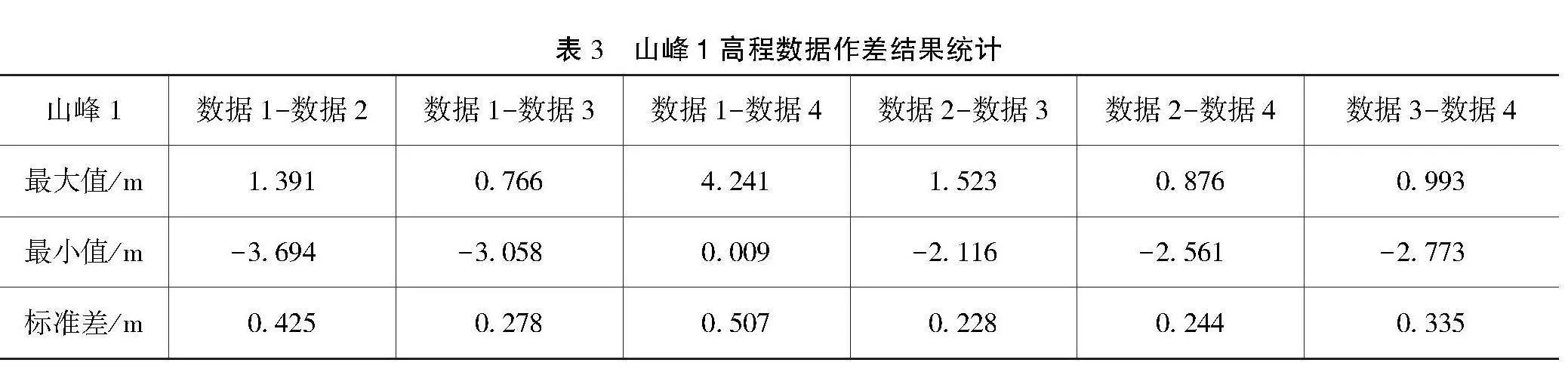
本文通过对山峰1的4次不同飞行高度、不同飞行路线的数据进行差值计算，得到了6组高程差数据；对这些高程差数据分别进行了最大值、最小值和标准差3种参数的统计分析。统计结果如表3所示。

通过对山峰1的作差参数进行统计，研究者可以得出一些关键的结论。数据2与数据3以及数据2与数据4的误差分布表现出相对较为集中的趋势，高程差主要分布在较窄的范围内，为-0.5 m～0。这表明2组数据之间的地形相对较为稳定，高程变化较为一致。相比之下，数据1与数据4的误差分布则呈现出相对分散的特征，高程差误差的范围较为广泛，达到了0.009～4.241 m，这表明数据1与数据4之间的高程差相对复杂。此外，数据3相对于其他几组数据，其误差相对较小，山峰1中的数据3的高程数据相对稳定。数据1与其他几组数据之间的误差最大，尤其是与数据4之间的高程差异最为显著。

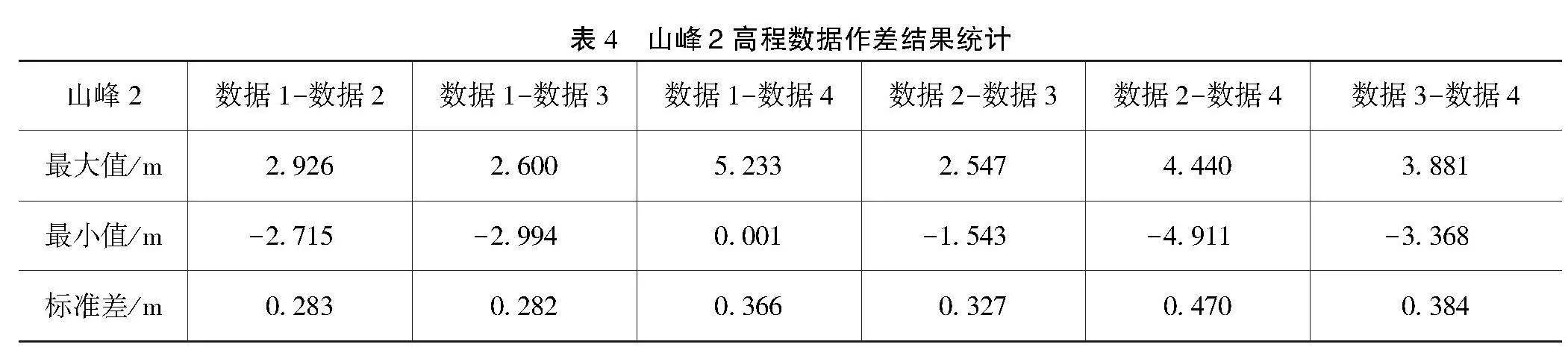
下面对山峰2的4次不同飞行高度、不同飞行路线数据的高程数据进行交叉作差，根据最大值、最小值和标准差3种参数对所得的数据进行统计分析，具体的统计结果如表4所示。

通过对山峰2的作差参数进行统计，本文可以得出一些关键结论。数据2、数据3和数据4之间的高程差误差分布表现出相对集中的趋势，高程差主要分布在较窄的范围内，接近于0。这表明3组数据相对稳定，高程差变化较为一致。然而，在参数统计中，数据1与数据2、3之间的高程差值参数统计结果较小。同时，从高程差的最大值与最小值的统计结果可以看出，在山峰2的数据2、数据3和数据4中存在个别点的高程差值较大的问题，影响整体参数的统计结果。剔除个别误差较大的点后，数据2与数据3的高程数据更为准确。

根据山峰1与山峰2不同飞行高度下高程差的统计结果，本文可以观察到山峰1的高程变化比山峰2更为显著。这表明在山峰1的地形中，高程的变化范围更广，可能存在更为复杂和多样化的地理特征。进一步分析高程差参数的统计结果可知，山峰1与山峰2的高程变化呈现出不同的趋势。在山峰1的地理特征下，高程变化更大，在高程误差的统计结果中，表现为较大的标准差和更广泛的误差分布。相比之下，山峰2的高程变化相对较小，其地形可能更加稳定和一致，因此误差分布更为集中且标准差较小。这种趋势表明：在地形高程变化较大的地理特征下（例如山峰1），可能存在更大的高程误差。综上所述，在山峰区域中，第3次数据的无人机飞行数据最为精确，同时高程变化越小，该区域的无人机数据越准确。

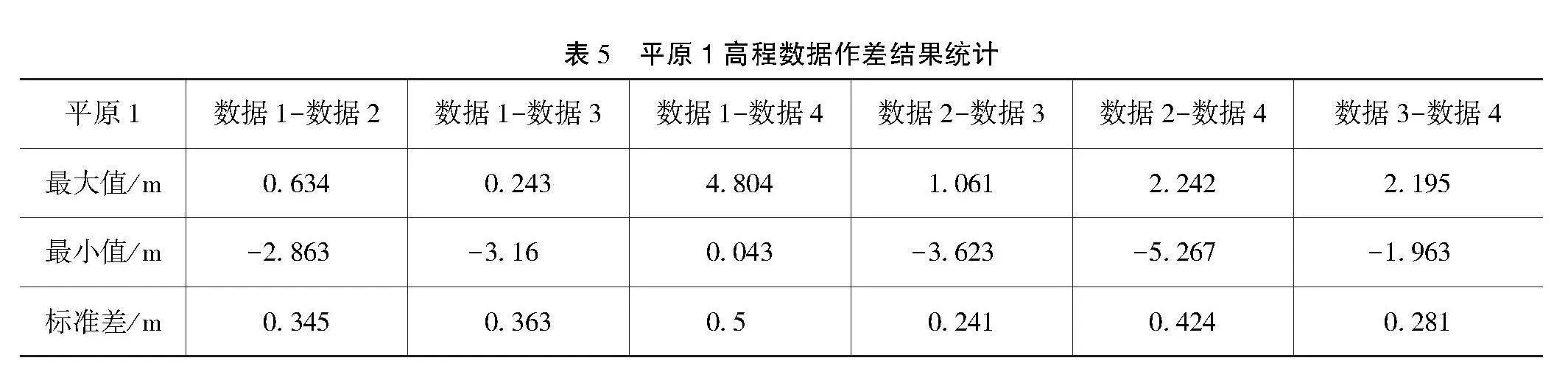
对平原1的4次不同飞行高度、不同飞行路线的数据进行差值计算，本文可得6组高程差数据。对这些高程差数据进行最大值、最小值和标准差3种参数的统计分析，结果如表5所示。

由高程数据的标准差统计结果可知：数据1与数据4之间的高程差异最为显著，达到0.500 m，其差值范围从4.804 m变化至0.043 m；数据2与数据4以及数据1与数据3之间的高程差异也相当显著，标准差分别为0.424 m和0.363 m；相比之下，数据3与数据4以及数据2与数据3之间的高程差异较小，标准差分别为0.281 m和0.241 m，差值范围也较为稳定；数据1与数据2之间的高程差异略大于数据3与数据4之间的差异，其标准差为0.345 m。综上所述，数据2与数据3的高程值最为接近，同时，数据3的高程值与其他几组数据的标准差均较小，因此，数据3的高程值更为稳定；数据1与数据4的高程差异的标准差最大，表明两者之间的高程数据相差最大。

根据平原1的数据分析结果，研究者发现该区域的高程值与其他地区相比存在较大的误差，其分布范围更广。特别是与数据4相比，平原1的高程值明显偏高。相比之下，数据3与其他数据组的高程差异最小，这表明其高程值相对稳定。此外，平原1与数据4之间的高程误差最大，进一步凸显了该差异。因此，本文可得如下结论，数据3在高程值的稳定性方面表现出色，而平原的数据1与数据4之间存在明显的高程差异。

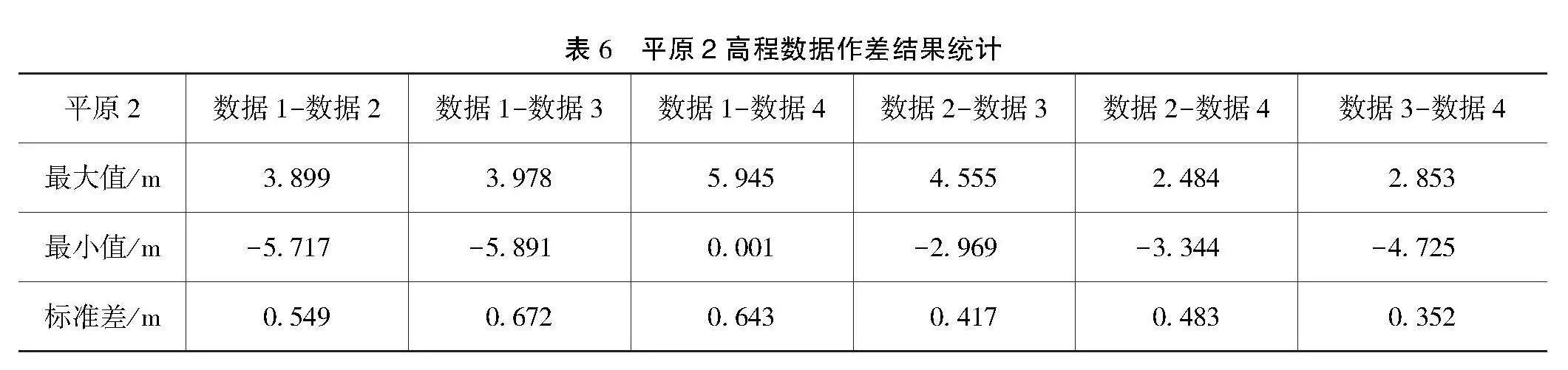
对平原2的4次不同飞行高度、不同飞行路线的数据进行差值计算，本文可得6组高程差数据。对这些高程差数据进行最大值、最小值和标准差3种参数的统计分析，结果如表6所示。

在平原2中，数据1与数据3之间的高程差异最为明显，其标准差可达0.672 m，差值范围最宽广，从3.978 m变化至-5.891 m。这说明数据1与数据3之间的高程差值极为显著。数据1与数据2以及数据1与数据4之间的高程差异也相当明显，标准差分别为0.549 m和0.643 m。相比之下，数据2与数据3以及数据3与数据4之间的高程差异较小，标准差分别为0.417 m和0.352 m，差值范围也较为稳定。数据2与数据4之间的高程差异略大于数据2与数据3之间的差异，其标准差为0.483 m。

在平原地形下，数据3的高程值与其他几组数据的高程值误差最小，因此其高程数据可靠性最高。数据2的高程数据虽稍大于数据3的差异，但仍相对可靠。相反，数据1的高程数据均大于数据4，且与其他组数据相比，其高程差分布范围最广，这表明其高程数据不稳定。对比平原1与平原2不同飞行高度获得的无人机数的高程数据，本文发现平原1的高程数据标准差变化小于平原2，这说明平原1的地形更为平缓。由高程差数据的各参数进行统计分析可知，平原1的高程数据更为准确。

各种地形区域的高程数据变化程度存在明显差异。平原地形的高程变化最为平缓，而山峰的高程变化最为显著。在不同地形区域中，本文可以通过高程数据的最大值、最小值以及标准差来评估其高程变化情况。标准差越大，意味着各区域的高程分布范围越广，高程数据的误差也越大。因此，平原区域的高程数据误差通常较小。进一步比较各区域之间的高程数据可靠性，本文发现标准差越小，高程的误差越小。在山峰区域中，山峰2的高程数据误差较小；而在平原区域中，通过误差分布直方图可以清晰地看出，在该地形特征下，平原1的高程数据表现最为稳定。同时，对比各区域的高程差值，数据3的数据最为准确。综上所述，不同地形区域的高程数据特征各异，通过分析最大值、最小值和标准差等参数，本文能够更好地评估和理解各区域的高程变化情况及数据可靠性。

3" 基于无人机倾斜摄影测量高程对比分析应用

根据不同飞行高度无人机高程对比分析结果，与其他3次无人机数据进行高程数据对比，第3次无人机高程数据最为稳定。因此，本文选取第3次无人机飞行数据进行无人机高程对比分析应用。

此次飞行的拍摄点高程分别为1222.6 m与1249.1 m，同时，采用80%的航向重叠率和80%的旁向重叠率。该分析区域中部地区为山谷，在山谷中有一条公路穿过该区域，在公路西部有一条干涸的河流，为李家塔峁底沟；该区域的西部与东部为山峰。

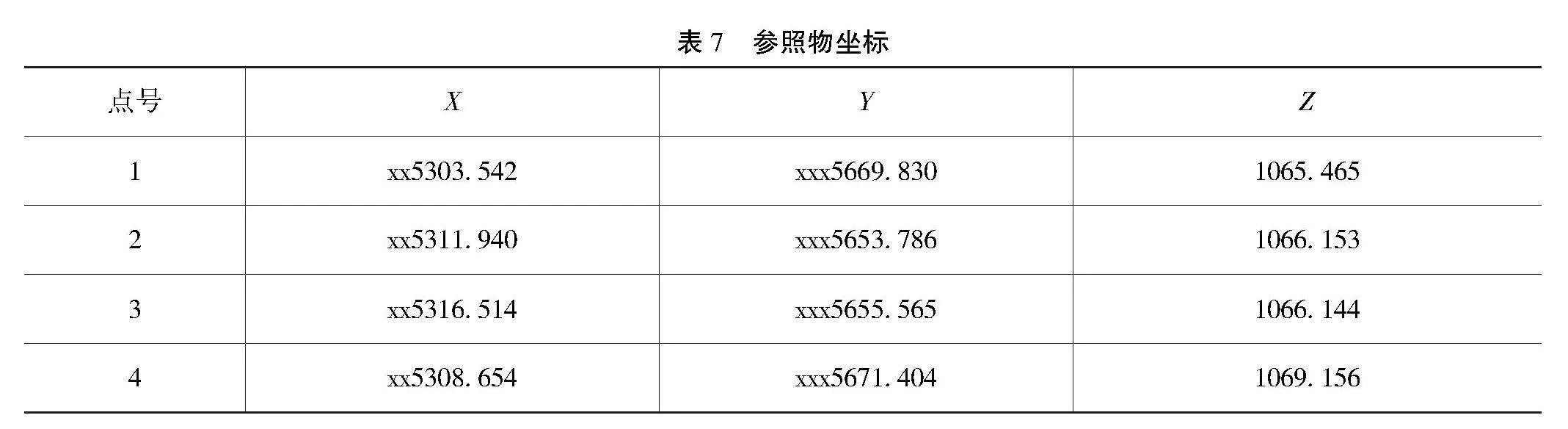
选取该分析区域中部的房子作为参考物，进行分析区域匹配，利用CAD画图软件对该参照物边界进行4点一般房屋的图层画图，表7为该参照物边缘坐标。

本文通过该点在无人机获取的图像中画出该参照物的边缘轮廓，在该分析区域的井上下图中找到该参照物的图像；通过该参照物，将井上下图层与无人机图层进行重合操作；在井上下图中选取与无人机图像相同的等高线区域。

本文对获取的高程图像进行网格划分以获取在网格上的高程值，网格划分方法是由给定的网格间距值dl确定横纵方向的网格节点数，同时计算出网格的间距值。其中，横向网格数为［8］：

n=intxmax-xmindl+1

横向网格间距为：

dx=xmax-xminn-1

纵向网格数：

m=intymax-ymindl+1

纵向网格间距值为：

dy=ymax-yminm-1

对于生成的网格，本文采用方位加权法求取该网格点上的高程值。方位加权法是一种常用的数据插值方法，其可以通过在给定点周围的区域内取点并进行加权平均来估计该点值。为了获得更准确的估计结果，本文可以将区域划分成若干个象限，从每个象限内取一点进行加权平均。

本文可以将平面以（x，y）为原点划分成4个基本象限，再将每个象限等分为n0份，这样整个平面就被划分成4n0等份。在每个等分角内寻找距离（x，y）最近的数据点，将其z值记为zi1，其到点（x，y）的距离记为ri1。最后，（x，y）的值可以表示为［8］：

Z（x，y）=∑4n0i1=1Ci1·Zi1

其中Ci1公式如下：

Ci1=4n0j=1

j≠i1r2l∑4n0k=14n0l=1

l≠kr2l

该方法的优势在于可以获得在观测数据点附近变量的小尺度趋势，从而更好地反映数据的局部特征。方位加权法可以快速求得高程点数据。

本文对研究区域生成的格网如下：以15 m为边长生成格网，x方向各网点数为51，y方向各网点数为31，x方向边长为15.009 m，y方向边长为15.017 m，提取该网格点上的高程数据。

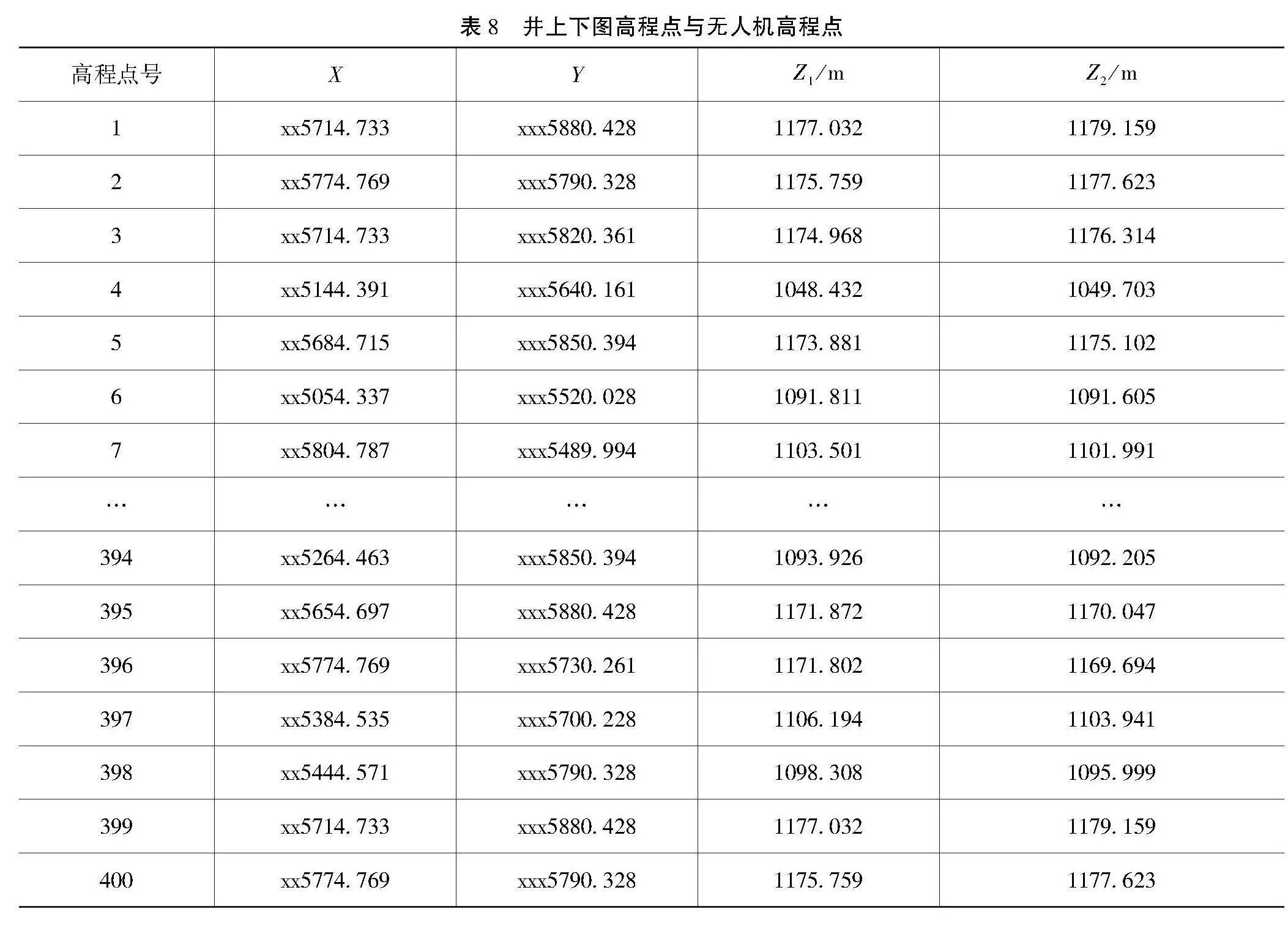
本文对高程数据进行误差分析，删除边界区域多余的高程点，获得了400组高程数据，如表8所示。表中，Z1为井上下图的高程值，Z1为无人机图像生成的高程点。

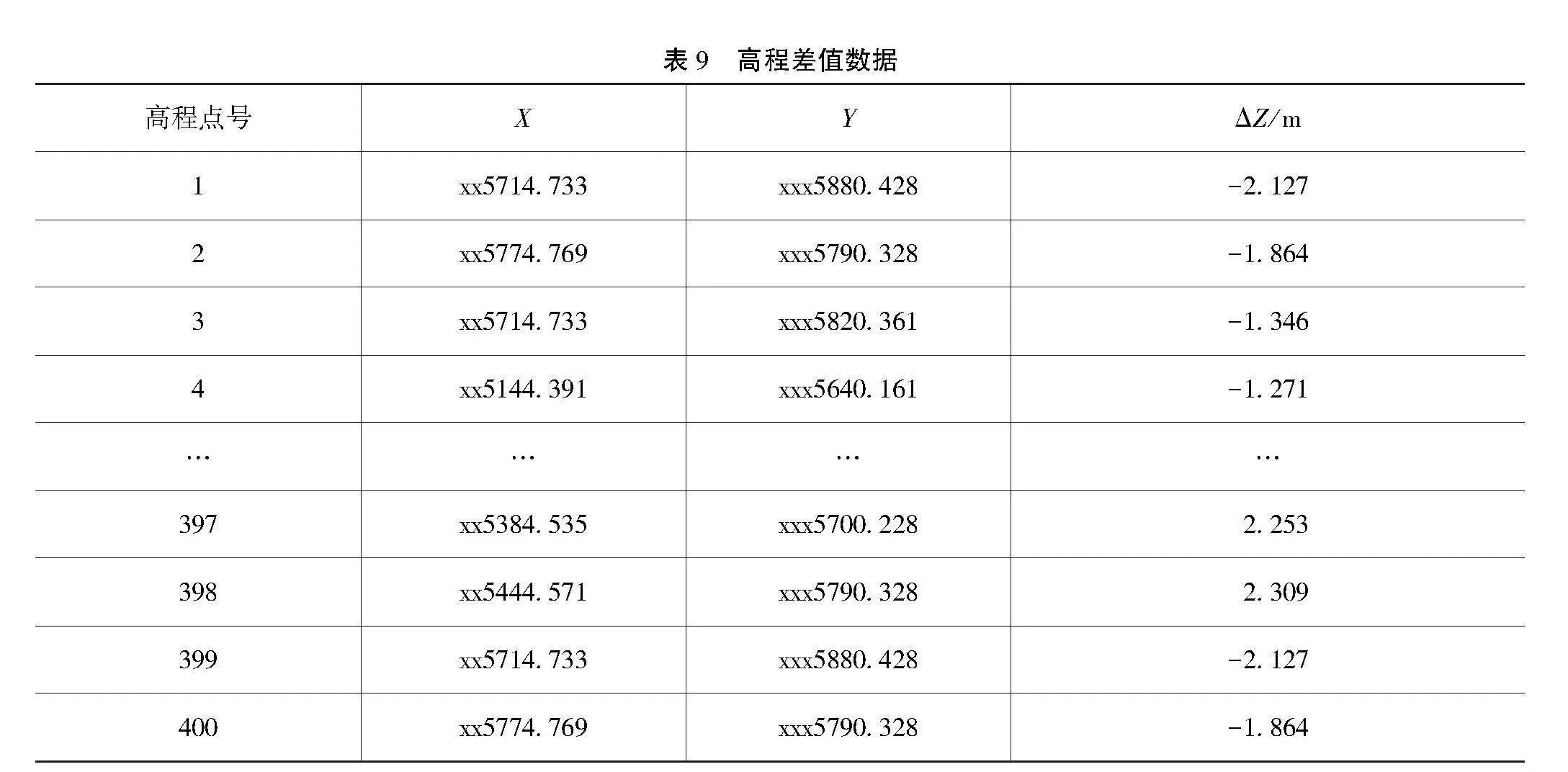
井上下图与无人机数据差值结果如表9所示。其中ΔZ为井上下高程值与无人机高程值的差值，通过获取高程值的差值计算可以得到沉陷区域。

本文对下沉等值线进行滤波处理，可以看出：在该区域中由于开采导致该地区地表下沉；同时，在该地区的两山之间，为山谷区域，该地区处于滑坡地区，由于岩石的滑动改变了地形地貌，该区域的高程上升。综上所述，在该区域中部地区由于开采下沉程度较大，该区域西部地区也产生了不同程度的下沉，但下沉程度小于中部地区，该区域的东北部为山谷地形，由于滑坡导致该区域地表高度上升。

4" 结语

本文通过对研究区域数据的基本参数进行统计，可以得到最大值、最小值、平均值、标准差和相关系数等统计参数。这些参数对于分析高程数据的变化情况至关重要。在不同地形区域中，高程数据的变化程度存在明显差异。平原地形的高程变化最为平缓，而山峰的高程变化较为显著。本文进一步比较各区域之间的高程数据可靠性，发现标准差越小，高程的误差也越小。在山峰区域中，山峰2的高程数据误差较小；而在平原区域中，平原1的高程数据表现最为稳定。同时，通过对比不同飞行高度的各区域的高程差值，本文最终得出，数据3的准确性最高。通过对沉陷区域的分析，本文肯定了无人机获取的高程数据的准确性；运用无人机数据可以获取不同矿区准确的高程数据，有利于对沉陷区域的分析。

参考文献

［1］庄振禄.无人机摄影测量及在城市规划中的应用［J］.城市建设理论研究（电子版），2023（26）：4-6.

［2］雷添杰，李长春，何孝莹.无人机航空遥感系统在灾害应急救援中的应用［J］.自然灾害学报，2011（1）：178-183.

［3］纪景纯，赵原，邹晓娟，等.无人机遥感在农田信息监测中的应用进展［J］.土壤学报，2019（4）：773-784.

［4］樊娇，雷涛，韩伟，等.无人机航迹规划技术研究综述［J］.郑州大学学报（工学版），2021（3）：39-46.

［5］张慧莹，董春来，王继刚，等.基于Context Capture的无人机倾斜摄影三维建模实践与分析［J］.测绘通报，2019（增刊1）：266-269.

［6］星锋锋.基于Context Capture软件的倾斜实景三维模型制作技术探讨［J］.科技与创新，2022（17）：4-6，9.

［7］丁夏萌.基于开源数据的资源三号境外DEM高程精度评价研究［D］.兰州：兰州交通大学，2023.

［8］康建荣.空间信息常用数值计算方法VC++实现［M］.北京：科学出版社，2016.

（编辑" 王永超）

Elevation comparison analysis and application of mine topography

based on UAV inclined photography measurement

WANG" Haoyu， KANG" Jianrong， ZHU" Bishang

（School of Geography， Geomatics and Planning， Jiangsu Normal University， Xuzhou 221116， China）

Abstract： This paper takes the Maodi coal mine in the east foothill area of Luye Mountain， Aojiawan Township， Xing County， Shanxi Province， as the study area to carry out the comparative analysis of elevation based on unmanned aerial vehicle（UAV）inclined photogrammetry. The UAV images are modelled in three dimensions to obtain a three-dimensional model. The elevation data are generated and elevation point matching is performed. The elevation comparison analysis is carried out for each area under different flight altitudes， and the parameters of each area are counted to analyze the terrain characteristics and elevation change characteristics of different areas. The difference of elevation data is calculated， the parameters of the difference data are calculated， and the reasons for the data error are analyzed. The analysis area is selected for subsidence analysis.

Key words： UAV inclined photogrammetry; 3D model; elevation comparison; subsidence analysis