基于审美能力培养的初中数学教学设计

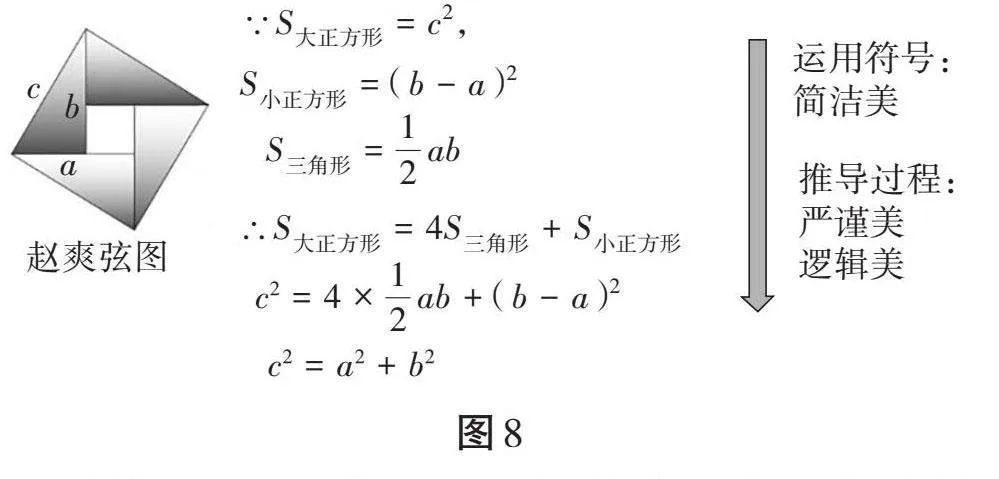
［摘 要］追求数学美，是数学发现的重要因素。数学审美教育，既符合数学对象的美学特征，又能培养学生的数学审美能力，提升学生的数学核心素养。文章以人教版八年级下册“勾股定理”一课为例进行基于审美能力培养的教学设计，为教师培养学生数学审美能力提供参考与借鉴。

［关键词］审美能力；初中数学；教学设计；勾股定理

［中图分类号］" " G633.6" " " " " " ［文献标识码］" " A" " " " " ［文章编号］" " 1674-6058（2024）24-0024-04

追求数学美，是数学发现的重要因素［1］。在不同版本的初中数学教材中，均可以看到一些关于数学美的例子，如北师大版八年级上册“实数”这一章展现了“毕达哥拉斯螺线”，通过图形展示数学美；人教版八年级上册“对称轴”一课通过挖掘自然景观、艺术作品等现实事物的对称元素，让学生体会生活中的数学美。对数学美进行研究，实施数学审美教育，可使学生体验知识的多样性，开阔学生的学习视野，激发学生的学习热情，培养学生的审美能力。

《教育大辞典》指出，美育亦称“审美教育”，是学生掌握审美基础知识、形成一定的审美能力、培养正确的审美观点，美化心灵、行动、语言、体态，提高道德与智慧水平的教育［2］。正如英国教育家斯宾塞所说：“没有审美价值，教育过程就失去一半的美好意义。”将美育寓于数学教学之中，把教学活动转化为审美活动，让学生成为审美的主体、摄取知识的主体［3］，学生会感到学习数学很快乐，并能发现事物之间存在的内在数学关系，唤醒学习数学的内在需求，进而提高审美意识和能力。对于数学审美能力，一方面可通过引导学生主动学习数学知识、参与数学实践来培养，另一方面可通过进行数学审美教育来培养。

本文选取人教版八年级下册第十七章第一课时“勾股定理”进行基于审美能力培养的教学设计。

一、教学设计

（一）创设精美情境，发现数学美

生活中蕴含着丰富多彩的数学美学元素，教师可以从常见的物体、现象出发，巧妙创设问题情境、民族文化情境等各种教学情境，让学生从中发现生活中的数学美，激发学生的学习兴趣。

师：请同学们欣赏一下2002年国际数学家大会的会徽（如图1）。

师：这个图案是赵爽弦图，它是由哪些几何图形构成的？

生1：它中间有一个小正方形，四周是四个直角三角形。

师：利用简单的几何图形可构建一些漂亮的图案，甚至是美化建筑形体。我们身边还有哪些由直角三角形或者其他几何图形构成的图案或建筑呢？

生2：奥运五环、窗户、拉闸门……

师：我们的生活中有许多漂亮的图案和建筑都是由一些几何图形组合形成的，不同的几何图形蕴含着不同的数学知识、文化。那么在赵爽弦图中到底蕴含什么数学知识呢？下面我们一起来学习本节课的知识。

设计意图：联系生活，创设精美情境，并设置问题，引发学生思考。将实际与理论相结合，使学生明白数学的应用价值，促进学生学会用审美的眼光去感受生活中的数学，进而培养学生的感知能力和审美能力。

（二）挖掘数学史料，感悟数学美

1.提出命题

教师利用多媒体展示数学史料：相传在2500年以前，古希腊著名数学家毕达哥拉斯在朋友家做客时，发现朋友家的地砖反映了直角三角形的三边关系（如图2）。

师：同学们，你们能找出地砖图案中存在的等量关系吗？我们要怎么做，才能简洁地表达出相应的关系？

生3：可以先把一部分地砖提取出来，分别用字母A、B、C表示（如图3），这样就能简洁表达了。

师：很好！接下来请观察正方形A、B、C，你们发现了什么？

生4：正方形A、B的面积等于正方形C的面积。

师：如何用数学符号表示这样的关系？

生4：[SA+SB=SC]。

师：相比用文字描述，用数学符号表示有什么优势？

生5：用数学符号表示更简洁，更便于计算。

师：没错！将文字语言转化为符号语言，就是数学的简洁性和抽象性表达，便于我们对某一问题、规律的理解和探究。

（教师进行板书，如图4所示）

设计意图：引入数学史料，引导学生了解勾股定理的来源以及发展规律，让学生体会数学的严谨性，感悟数学的形态美和过程美。构造特殊图形，引导学生发现其中蕴含的数学思想，感受数学的奇异美。从文字语言到符号语言，渗透数学符号意识，让学生体会数学的简洁美、理性美，从而培养学生的审美能力。

接下来，教师把地砖的图像抽象出来放在网格中，研究它们到底有什么关系。

探究1：观察图5，有三个正方形A、B、C，它们围成一个三角形，假设小方格的边长为1，那么正方形A、B、C的面积各是多少？它们之间有什么关系？请用算式表示。

生6：正方形A的面积为9，正方形B的面积为9，正方形C的面积为18，得出[SA+SB=SC]。

师：正方形C的面积是如何计算出来的？

生7：利用割补法将正方形C分成四个三角形。

师：是的，利用割补法可以解决这一问题，这是在边长为特殊值的情况下得到[SA+SB=SC]，令正方形A、B、C的边长分别为[a]、[b]、[c]，其中[a=b]，那么[SA=a2]，[SB=b2]，[SC=c2]，则对于等腰直角三角形就有[a2+b2=c2]这样的性质。

师：其他直角三角形是否有这样的性质呢？

探究2：观察图6，假设小方格的边长还是1，正方形A、B、C的面积各是多少？此时它们又有什么关系？

生8：正方形A的面积为16，正方形B的面积为9，正方形C的面积为25，得出[SA+SB=SC]。

师：所以对于任意直角三角形有这样的性质：两直角边的平方和等于斜边的平方。若直角三角形的两直角边长分别为[a]、[b]，斜边长为[c]，则有[a2+b2=c2]。

设计意图：由等腰直角三角形到任意直角三角形，从特殊到一般，引导学生总结规律，让学生感受数学的逻辑美和奇异美，培养学生观察、概括、分析等方面的能力，提高学生解决问题的能力。通过探究活动，引导学生体会数与形的转化，感受数学的简洁美和对称美。

2.验证命题

师：如果直角三角形的两直角边长分别为[a]、[b]，斜边长为[c]，那么是否有[c2=a2+b2]？如何证明这个命题？

师：可以利用赵爽弦图，采用面积法来证明。根据已知条件，可以列出什么等式？

生9：通过观察图形发现，大正方形是由四个小三角形和一个小正方形组成（如图7），它们的面积关系为[S大正方形=4S小三角形+S小正方形]。

师：根据已知条件，可以列出a、b、c的关系式吗？

生10：大正方形的面积[S大正方形=c2]，小正方形的面积[S小正方形=（b-a）2]，三角形的面积[S三角形=12ab]，因此可列出式子[c2=4×12ab+（b-a）2]，化简得到[c2=a2+b2]。

师：经过证明就得到了今天我们所要学习的勾股定理，即若直角三角形的两直角边长分别为[a]、[b]，斜边长为[c]，则有[a2+b2=c2]。

（教师板书，如图8所示）

设计意图：让学生体验数学并不能凭感觉得出结论，而是需要经过逻辑推理和严谨证明。在“猜想—验证—形成数学定理”的过程中，将烦琐的文字语言转化为符号语言，体现数学的逻辑美、严谨美和抽象美，促进学生简单化、符号化、严谨化地解决问题。教师通过板书，规范书写过程，塑造美的教学形象。

（三）深入探究知识，创造数学美

练习1：现有一个宽为1米、高为2米的门框，如果一块长为2.5米、宽为2.2米的长方形薄木板想从此门框通过，请问它能否顺利通过？为什么？

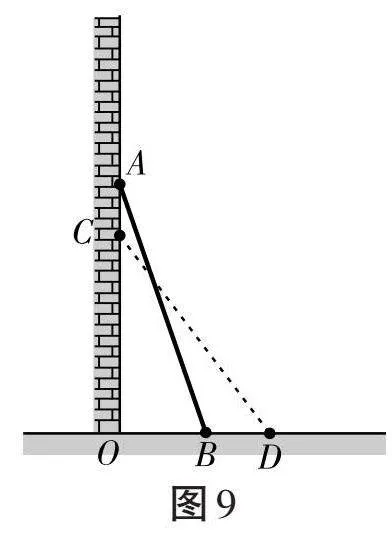
练习2：如图9，一架3米长的梯子AB斜靠在一竖直的墙AO上，这时AO为2米。如果梯子的顶端沿墙下滑0.2米（如图中CD），那么梯子的底端也外移0.2米吗？

师：通过以上练习，你能总结出什么解题方法？

生11：先分析题目是否设计有直角三角形，找到直角三角形的两条边长条件，利用勾股定理求出第三边的长度，进而求得目标值。

师：没错！在解决问题时，我们通常先将题目所给的重要信息提炼出来，再把相似的问题放入一个数学模型中，利用熟悉的模型解决问题。

练习3：观察勾股定理公式，它的外显形式很美观（简洁、对称、统一），你能领会它的内在美吗？你还能列举比勾股定理公式更美的公式吗？你学过的最不美的公式有哪些？请说出你的理由。

设计意图：设置三个练习题，让学生运用勾股定理解决具体问题，并运用数学的统一性总结解题方法，构建知识体系。在书写时注意体现数学的简洁美及过程的严谨美、逻辑美，在现实问题与数学问题的转化过程中体现数学的内在理性美。引导学生观察勾股定理公式，体会它不仅形式上简洁、对称，而且能严谨地表示三角形三边的特殊关系，具有数学的简洁美和对称美。设置练习3，让学生联想所学公式，对比各个公式存在的数学美，指出其中的内在理性美和外在显性美，有效提高学生的审美能力。

（四）深化数学思维，欣赏数学美

师：这节课你们学到了什么，感悟到了什么？

生12：我学到了勾股定理，感受到它研究的是直角三角形的三边关系，知道线段在组成特殊结构时会产生漂亮的图案或公式。

生13：我学会从现实生活场景中抽象出数学问题，并形成猜想，感受到数学是无处不在的。

生14：我知道了我们所提出的猜想必须进行严谨的、合乎逻辑的、符合事实的证明，才能验证其正确性，并把正确的命题称作定理。在解决问题时，我发现要阅读并提取所给的重要信息，把相似的问题放入一个数学模型中，这让我感受到了数学具有统一性，以及利用定理、公式计算的奇异美。

师：勾股定理在今后学习的三角学中具有重要的作用，我们还可以利用口诀来记忆一组常见的勾股数“3，4，5”，即“勾三股四弦五”。所以说，数学是一门奇妙的学科，数学知识可以借助符号、图形甚至是口诀来记忆。

师：数学无处不在。会徽中，简单几何图形的构造蕴含着勾股定理；生活中，利用几何图形构造的服饰图案、建筑比比皆是。请大家欣赏这张图片（如图10），它是不是也蕴含几何图形的变化关系呢？

师：这张图片展示的是瑶族服饰上的图案，展现了瑶族人民精湛的技艺和对美的追求。不同的图案寄托着瑶族人民不同的情怀。我们可以观察到最里面的图案是由直角三角形围成的正方形，这些漂亮的图案中蕴含线段之间、三角形边与边之间以及正方形对角线之间的关系。

师：那么由直角三角形或者其他简单几何图形还构成了哪些漂亮的图案、物品呢？请大家课后寻找，并思考其是否蕴含勾股定理或者其他数学知识，提取有关信息、设计数学问题并解答。

设计意图：通过课堂总结，促使学生对勾股定理进行深入思考和理解，感悟数学的内在理性美。教师提出口诀记忆法，促使学生明白知识的形成是追求美的过程，公式的美有利于对数学知识的记忆。以少数民族文化感染学生，渗透审美教育，培养学生的审美能力。

二、教学反思

学生数学审美能力的培养可从学生和教师方面着手。

学生作为学习的主体，应充分发挥自身的主观能动性，有意识地培养自身的数学审美能力。学生应积极参与教学活动，用寻找的眼光去探究数学规律、总结数学知识，结合数学美的特征和规律学习数学［4］，更好地理解数学美的内涵，提高数学审美能力。数学来源于生活，学生应细致观察身边的事物和自然现象，不断从数学美的角度探索事物，提高数学审美能力。学生还应主动挖掘数学课本、故事中的美学思想，加深对数学美的理解，促进数学审美能力的提升。

教师要做好“引路人”，引导学生领悟数学的美。教师应增强自身的审美意识，不断挖掘数学美，在传授学生数学知识的基础上有意识地渗透数学审美教育。对于数学美，学生的理解往往停留在表层，要想让学生更好地理解数学美，提高数学审美能力，教师要引发学生对数学的审美思考，使学生深刻体会数学美，同时为学生搭建创造美的舞台，实施数学审美教育，让学生成为数学学习的主人，使学生的数学审美能力得到全面提升。

［" "参" "考" "文" "献" "］

［1］" 邓清，盘梦.启于数学审美" 探得问题本质：基于2019年全国Ⅲ卷圆锥曲线试题的研究［J］.中国数学教育，2020（合刊2）：99-102，106.

［2］" 周庆元，胡绪阳.走向美育的完整［J］.教育研究，2006（3）：39-43，49.

［3］" 林华.彰显数学审美功能" 优化课堂教学效果［J］.初中数学教与学，2019（22）：1-2.

［4］" 李彦.例谈课堂教学中“数学美”的挖掘［J］.文理导航（下旬），2017（2）：39.

（责任编辑 黄春香）