基于随机场理论的隧道开挖后地表及隧道变形分析

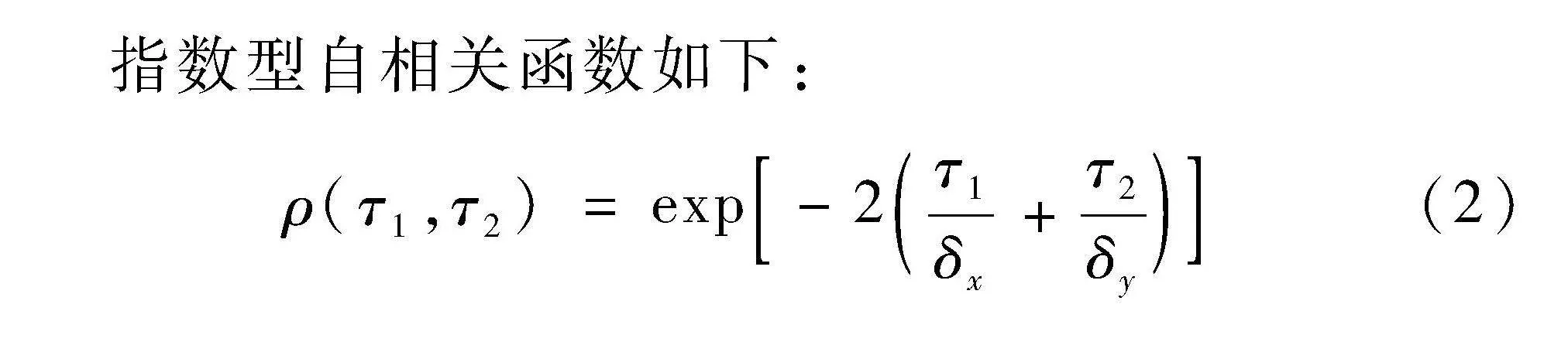
摘要：

天然土体由于受到多因素的影响，土体参数存在着内在的不确定性。为了更好地反映实际土体参数的分布情况，基于随机场理论，在考虑黏聚力和内摩擦角空间变异性的情况下，利用乔列斯基分解和随机有限元模型相结合的方法，对地表和隧道变形进行分析。研究结果表明：地表沉降曲线簇的波动范围随着黏聚力和内摩擦角相关距离的增大而增大，其竖直相关距离对地表沉降变形的影响更明显；黏聚力和内摩擦角的变异系数对地表沉降变形的影响强于其相关距离对地表沉降变形的影响；隧道变形值的分布随着黏聚力和内摩擦角变异系数的增大而逐渐离散，其中内摩擦角变异系数对隧道变形值分布的影响更明显；不考虑黏聚力和内摩擦角的空间变异性将偏小地预测地表沉降和隧道变形，使设计偏于危险。

关" 键" 词：

隧道开挖； 地表沉降曲线簇； 随机场; 空间变异性; 相关距离； 随机有限元模型

中图法分类号： U451

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.07.030

收稿日期：

2023-05-29

；接受日期：

2023-08-29

基金项目：

国家自然科学基金项目（41071049）;中国地震局工程力学研究所基本科研业务费专项资助项目（2021D13）;黑龙江省自然科学基金项目（LH2023D022）

作者简介：

王" 勤，男，硕士研究生，主要从事岩土工程方面研究。E-mail：w2670275199@163.com

通信作者：

柳艳杰，女，教授，博士，主要从事冻土工程、工程力学等方面研究。E-mail：Lyj@sina.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 07-0229-11

引用本文：

王勤，阎龙，张海莹，等.基于随机场理论的隧道开挖后地表及隧道变形分析

［J］.人民长江，2024，55（7）：229-239，253.

0" 引 言

岩土材料参数的变异性是岩土工程中的一个热点问题。因为受到沉积条件、应力历史以及风化条件等因素的影响，天然土体参数中存在着内在的不确定性［1］。在相关研究领域，随机有限元和随机有限差分方法是两种常用的随机场分析方法。使用随机场方法进行的工程问题分析主要集中在边坡工程［2］、地基沉降［3］、基坑开挖［4］等领域。为了更加准确地反映土体的空间变异性，Vanmarcke［5］提出了随机场理论，把空间中任意点的岩土参数看作随机变量，提出了一种新的方法，即用相关距离、相关函数描述随机场中点对点之间的相关性，并将其与空间联系起来。所谓关联距离，就是两个点之间的关系，在一定的关系范围内，这两个点的关系较强，反之，就是关系较弱或没有关系。张隆松等［6］提出考虑统计不确定性的基坑变形可靠度高效蒙特卡洛模拟方法，并将其应用到台北 TNEC 基坑变形可靠度分析中。易顺等［7］采用随机场描述基坑的土体刚度参数，研究了土体空间变异性对地表沉降和侧向位移的影响。王曙光等［8］引入随机场理论，考虑地基土体参数的空间变异性，对地基极限承载能力进行上限有限元分析。

盛建龙［9］等基于局部平均法等随机场基本理论，结合有限差分强度折减法及可靠度分析方法，研究了随机场模型的相关距离以及黏聚力变异系数对边坡可靠度的影响。Griffiths等［10］研究了土体参数的波动距离和变异系数对边坡失稳概率的影响。Cheng等［11］研究了不同的参数自相关结构对边坡风险评估的影响。针对边坡失效概率分析，程红战等［12］开展了考虑土体参数旋转各向异性相关结构的边坡稳定性分析。综上所述，科研工作者及工程人员在岩土体空间变异性方面进行了大量的研究工作，但也有不足的地方：以上研究大多集中于边坡工程、地基沉降、基坑开挖的领域，将随机场理论运用到隧道工程的研究较少；另一方面以上研究均是研究单一参数的空间变化特征，即研究参数的自相关性，并没有考虑土体多元参数的空间变化特征对宏观变形规律的影响。

鉴于此，为丰富随机场理论在岩土工程领域的应用场景，本研究将随机场理论运用到隧道工程并且进行参数敏感性分析，以变异系数和相关距离为主要研究参数，同时考虑了黏聚力和内摩擦角的空间变异性对地表沉降变形规律以及隧道变形规律的影响。最后利用统计方法，对不同工况下的地表变形值以及隧道变形值进行了统计分析，也为后续隧道盾构施工中的风险评估提供更科学合理的参数。

1" 隧道开挖随机有限元模型

1.1" 土体参数随机场

随机场理论是岩土力学研究领域中的一个重要分支［13］。从概率学的观点来看，随机场是一个随机过程的空间扩展。其中，均值、方差、自相关函数、参数波动范围和随机变量的分布形式都是建立随机场所必须的。本文利用乔列斯基分解的方法，对岩土进行参数随机场建模。其步骤如下：

（1） 建立一个标准正态随机样本矩阵。因为拉丁超立方样本可均匀地覆盖到概率分布的极限值，所以本文采用拉丁超立方样本构成独立标准正态随机样本矩阵η。

η=［η1 η2 … ηi］（1）

式中：i表示随机场单元的数目。

（2） 利用乔列斯基分解法［14］求解由各个随机单元组成的相关系数矩阵C的下三角矩阵L。

在不同的地区和环境中，土体的水平和竖直相关长度变化范围差异较大。综合文献，本文内摩擦角φ和黏聚力c的水平和竖直的相关长度区间取为δx为10～40 m，δy为1～3 m。又由于任意两点之间的相对距离低于1.5倍地波动范围时，不同的自相关函数之间存在着很大的差异，而在相对距离超过1.5倍地波动范围时，这种差异并不显著，因此选取指数型自相关函数的计算比较简便。

指数型自相关函数如下：

ρ（τ1，τ2）=exp-2τ1δx+τ2δy（2）

式中：τ1和τ2分别为随机场中任意两个单元的中心点在水平和竖直方向上的相对距离；ρ（τ1，τ2）为随机场的二维自相关函数。

（3） 根据式（3）建立相关标准高斯分布随机场HDx，y。

HDx，y=Lξ（3）

式中：x，y为随机场空间中点的位置坐标；L为自相关系数矩阵；ξ为标准正态随机样本矩阵。

（4） 建立相关非高斯分布随机场。在实际的工程中，土体的参数一般服从非高斯分布，通过等概率变换的方法，将相关标准高斯随机场转换为相关非高斯随机场。对相关标准高斯随机场取指数，得到土体参数对数正态随机场Hix，y。

Hix，y=expμlni+σlniHDix，y（4）

式中：μlni 和 σlni 分别为相应正态变量lni的均值和标准差。转换关系如式（5）所示：

σlni=ln1+σiμi2μlni=lnμi-12σ2lni（5）

式中：σi和μi分别为变量i的标准差和均值。

1.2" 有限元模型的建立

以深圳某地铁隧道为例，利用ABAQUS软件建立盾构隧道二维有限元模型，如图1所示。隧道外径为D=6 m，内径为5.7 m，衬砌厚度为0.3 m。考虑到模型的边界效应［15］，模型的长取42 m（隧道中心线左右各21 m，3.5D），高取30 m，隧道轴线埋深H=15 m。建立土体模型时，需约束左右边界水平方向位移，底面约束竖向和水平方向位移。

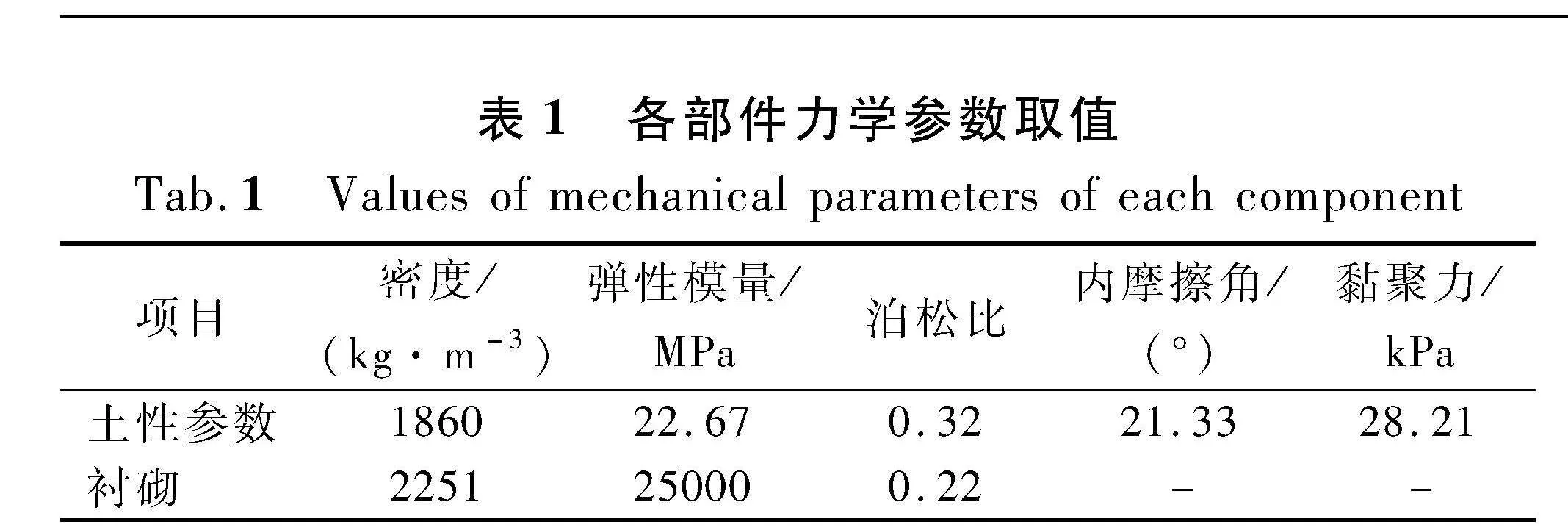
因为摩尔-库仑屈服准则仍然是数值计算中使用最多的一种方法，特别是在随机场地计算过程中，所以将土体视为满足摩尔-库仑屈服条件的理想弹塑性材料，衬砌为线弹性材料［16］。各参数详见表1。

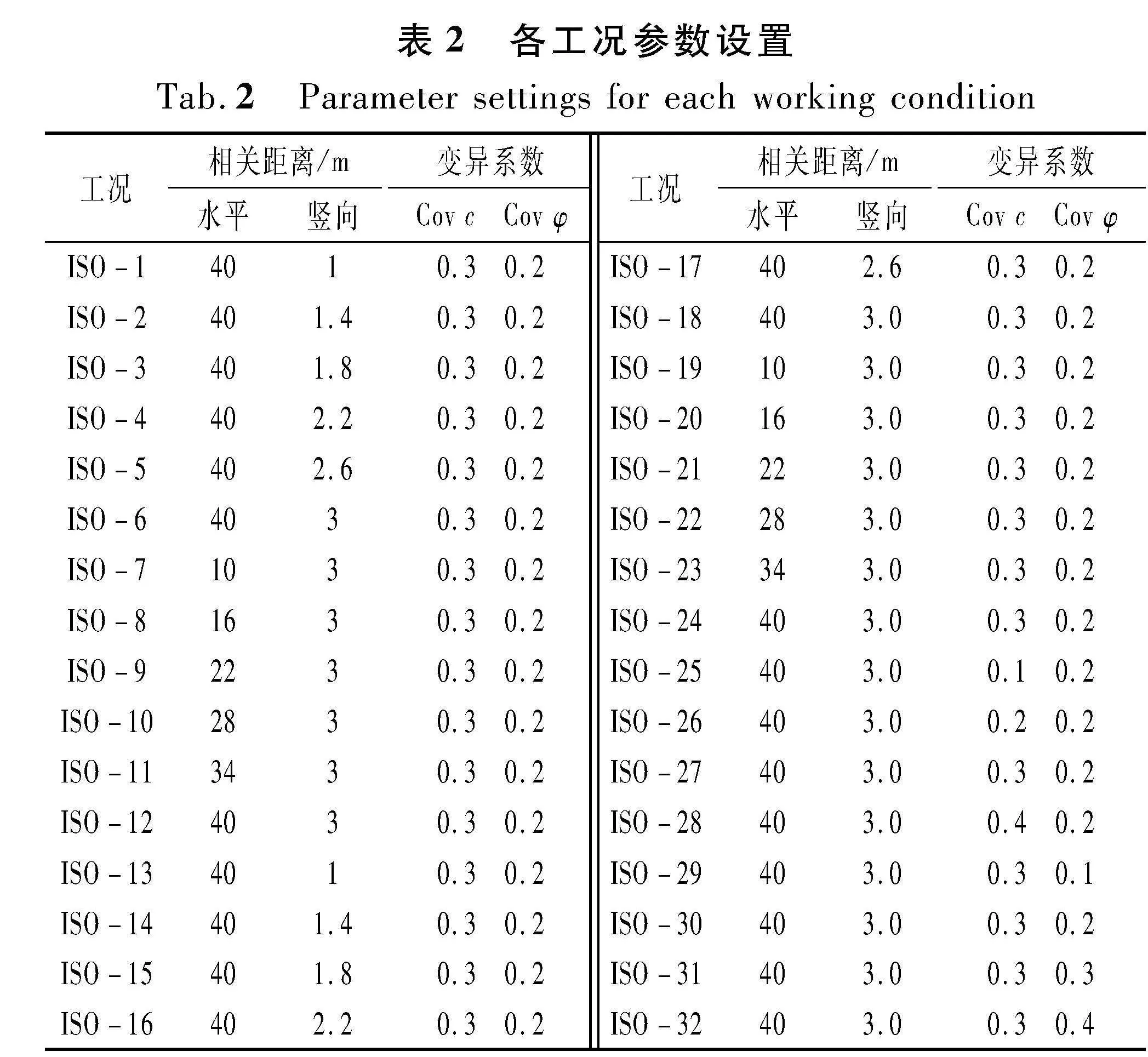
1.3" 工况设置

为探究土体不同相关距离和其变异系数条件下地表和隧道变形的规律，本文利用控制变量法，分别改变内摩擦角φ和黏聚力c的竖向相关距离、水平相关距离以及变异系数。需要注意的是，在进行参数敏感性分析时取ρc，φ=0［17］。为保证计算的准确性，每个工况模拟1 000次。表2中工况如下：工况ISO-1～ISO-6改变黏聚力竖向相关距离，工况ISO-7～ISO-12改变黏聚力的水平相关距离，工况ISO-13～ISO-18改变内摩擦角竖向相关距离，工况ISO-19～ISO-24改变内摩擦角水平相关距离，工况ISO-25～ISO-28改变黏聚力的变异系数，工况ISO-29～ISO-32改变内摩擦角的变异系数。

1.4" 随机场模型验证

为验证上述建立的随机场模型的准确性，通过选取某一随机场参数进行抽样统计分析，随机场抽样次数为1 000次。将这层土随机场内摩擦角φ和黏聚力c的均值和其变异系数随抽样次数的变化曲线分别绘制在图2中。随抽样次数的增加，土质的均值及变异系数逐渐稳定，内摩擦角φ和黏聚力c收敛于表1中随机场参数的给定值，变异系数也分别逐渐收敛于0.2和0.3，即侧面验证了所建立的随机场模型的准确性。

1.5" 数据处理框架流程

图3描述了空间变异性土体变形分析随机有限元法的数据处理流程。

2" 考虑黏聚力空间变异性的地表和隧道变形分析

2.1" 黏聚力不同相关距离

图4为ISO-1～ISO-6的参数分布云图以及地表沉降曲线。地面沉降曲线中的灰色实线是随机计算结果，红色的粗实线是地面沉降位移的包络线，红点划线是地面的平均沉降曲线，红虚线是确定性计算的结果。确定性是把土体视为均匀介质，也就是没有考虑到土体的空间变异性。从图中可以看出，每一次生成参数的随机场都不一样，所以地面沉降曲线也存在着一定的差别。与此同时，地表平均沉降曲线比确定性分析结果表现出了更大的沉降，因此可知不考虑c的竖直相关距离将导致较小的预测地表变形。而且当c的竖直相关距离在1～3 m增大时，地表沉降曲线簇的波动范围逐渐增大，但其波动范围的变化并不明显。

由图5（a）可知，从ISO-1到ISO-6，各工况地表最大沉降值均值从1.902 mm下降到1.884 mm，下降了0.94%。c的竖直相关距离在1～3 m逐渐增大时，其地表最大沉降值的均值先是出现下降然后在竖直相关距离大于2.2 m后均值未发生明显变化，这表明c的竖直相关距离在一定范围内变化时，对地表沉降值的影响有限。由图5（b）可知，随着c的竖直相关距离逐渐增大，地表最大沉降值的变异系数从0.473 6增加到0.515 3，增加了8.80%，由此可见，地表最大沉降值的分布随着c的竖直相关距离增大而逐渐离散。

同时，由图5（c）和（d）可知，c的竖直相关距离在1～3 m变化时，隧道各监测点变形均值没有出现明显的变化。其监测点B、C、D变形值的变异系数也没有出现明显波动。但A点变形值的变异系数从0.108 0增加到0.115 3，增加了6.76%，出现了相对明显的增长，因此在实际隧道施工时对拱顶的监测应更加密切。

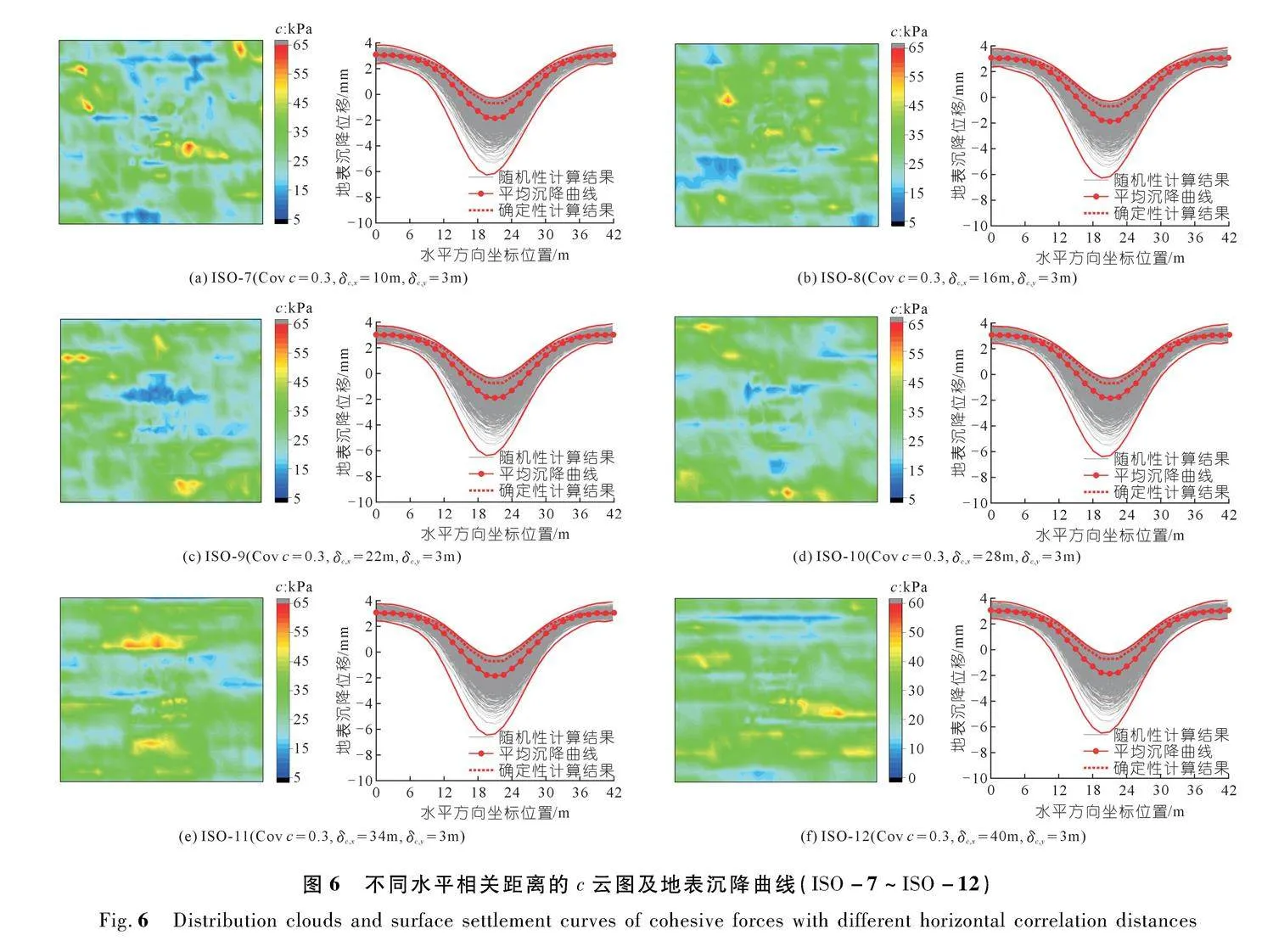
图6为ISO-7到ISO-12的参数分布云图以及地表沉降曲线。从图中可知，曲线簇形态跟图4相似。随着c的水平相关距离逐渐增大，地面沉降曲线簇分布逐渐离散，但都在其确定性分析结果附近随机波动，地表沉降曲线仍然符合正态分布曲线。地表平均沉降

曲线比确定性分析结果表现出了更大的沉降，由此可知不考虑c的水平相关距离将较小地预测地表变形。上述综合分析表明，c的相关距离对地表沉降变形的影响并不明显，本研究从其地表最大沉降值的均值和其变异系数能够更直观地看出地表沉降曲线簇中各曲线极小值点，即地表最大沉降值分布情况，从而推断出地表沉降曲线簇的波动范围随相关距离变化的规律。

由黏聚力的分布云图可知，随着相关距离的增大，参数云图呈现出不同程度的变化。当c的竖直相关距离在1～3 m逐渐增大时，其参数的竖向相关性逐渐增大，但是云图变化不明显，这跟其竖直相关距离波动范围较小有关。然而当c的水平相关距离在10～40 m逐渐增大时，可以明显看出参数水平向的连贯性及相关性有明显的提升。

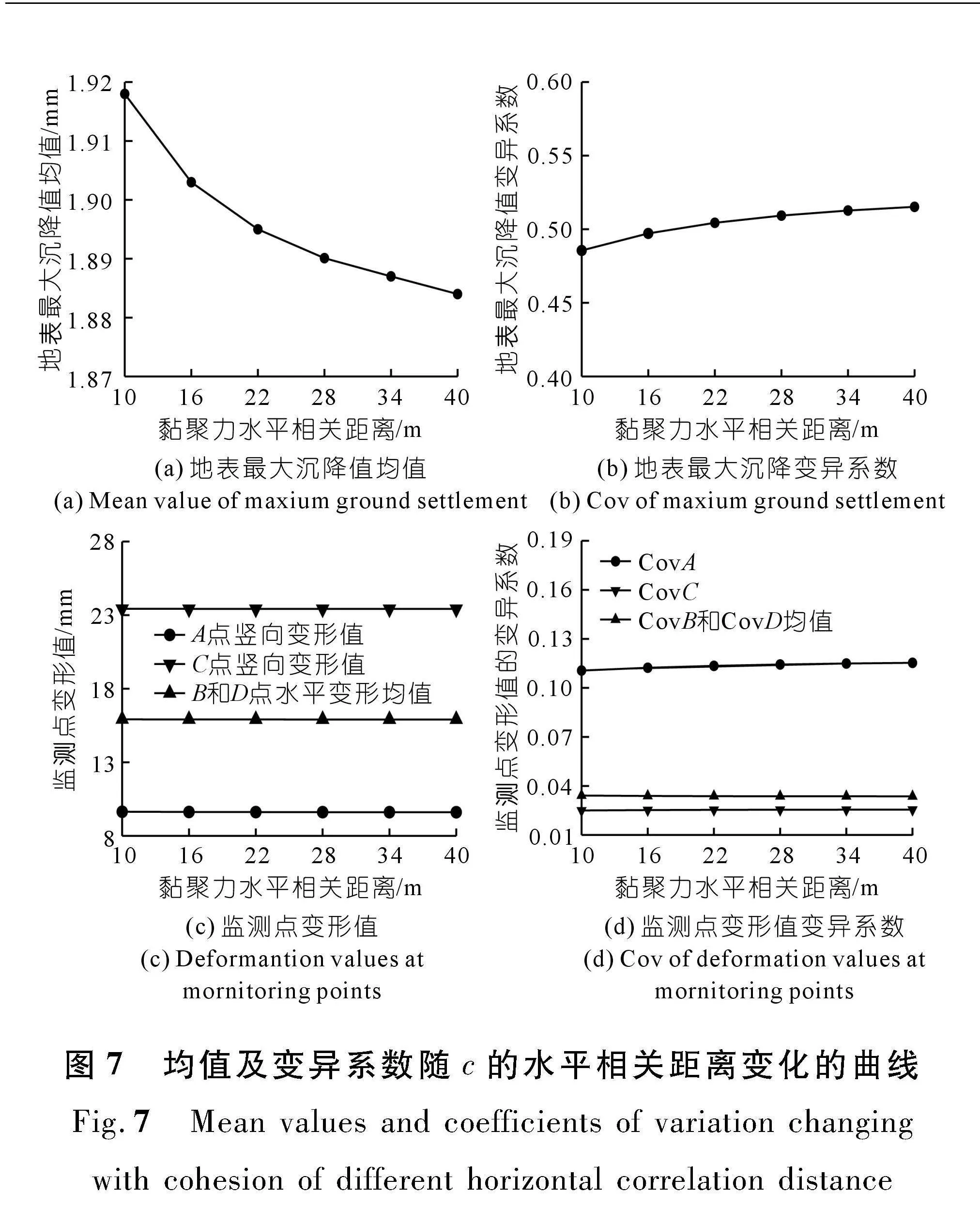
由图7（a）可知，ISO-7到ISO-12，地表最大沉降均值从 1.918 mm下降到1.884 mm，下降了1.77%。c的水平相关距离在10～40 m逐渐增大时，地表最大沉降值的均值整体出现下降，然而在其水平相关距离大于28 m后均值下降的速度开始减小。同时由图7（b）可知随着c的水平相关距离逐渐增大，地表最大沉降值变异系数从0.485 6增加到0.515 3，增加了6.12%。综上所述，地表最大沉降值的均值随c的相关距离增大而逐渐减小，水平相关距离对其均值的影响更大。由于其地表最大沉降值的变异系数能更好反映这一组数据的离散程度，因此本文研究地表变形的影响时主要考虑其数据变异系数的变化规律。c的竖向相关距离在1～3 m变化时地表最大沉降值变异系数增加了8.65%，而c的水平相关距离在10～40 m逐渐增大时，其地表最大沉降值的变异系数只增加了 5.97%。综合前文数据对比可知，地表沉降变形受c的竖直相关距离的影响更明显。

由图7（c）和（d），可知c的水平相关距离在10～40 m变化时，隧道各监测点变形均值仍然没有出现明显的变化，综上可知隧道监测点变形值受c的水平相关距离的影响较小。同时其监测点B、C、D变形值的变异系数也没有出现明显的波动。然而A点其变形值变异系数从0.110 6增加到0.115 3，增加了4.25%，出现了相对明显增长，因此在实际隧道施工时对拱顶的监测应更加密切。

2.2" 黏聚力c不同变异系数

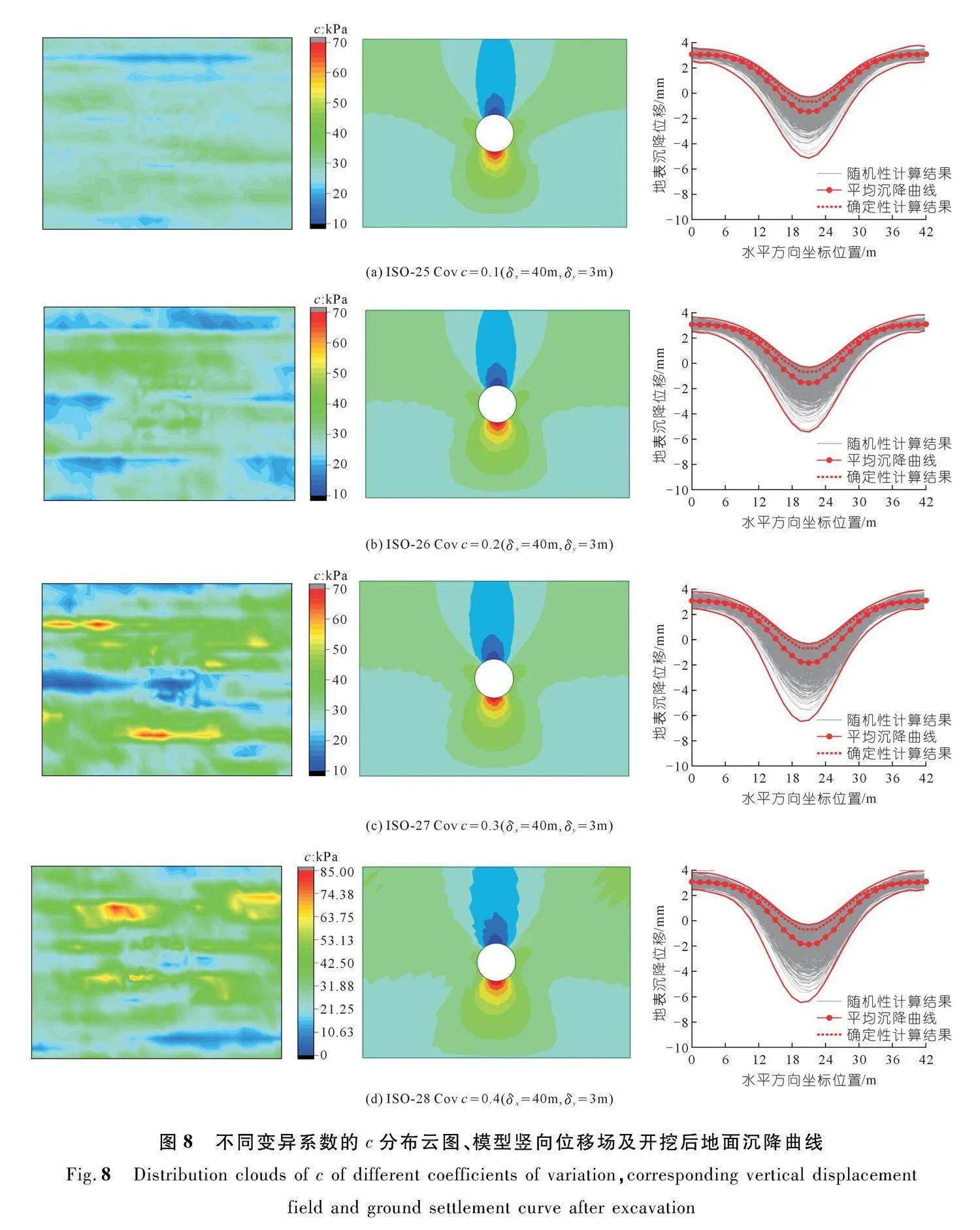
黏聚力c变异系数分别取0.1，0.2，0.3，0.4。对于每个值，采用乔列斯基分解法，随机模拟1 000次作为一组算例［19］。图8为黏聚力的分布云图、模型竖向位移场及开挖后地面沉降曲线。

由图8中云图可知，当变异系数从0.1增加到0.4时，其参数的不均匀性逐渐增加，随机场的参数波动范围也出现明显的增大。与此同时，随着变异系数增大，其竖向位移场逐渐呈现明显的不对称性，即宏观表现为地表沉降曲线的不对称性。此外当Cov c=0.1时随机场模型得到的地面沉降曲线簇相对更为集中，然而随着变异系数增大，地面沉降曲线簇逐渐离散。

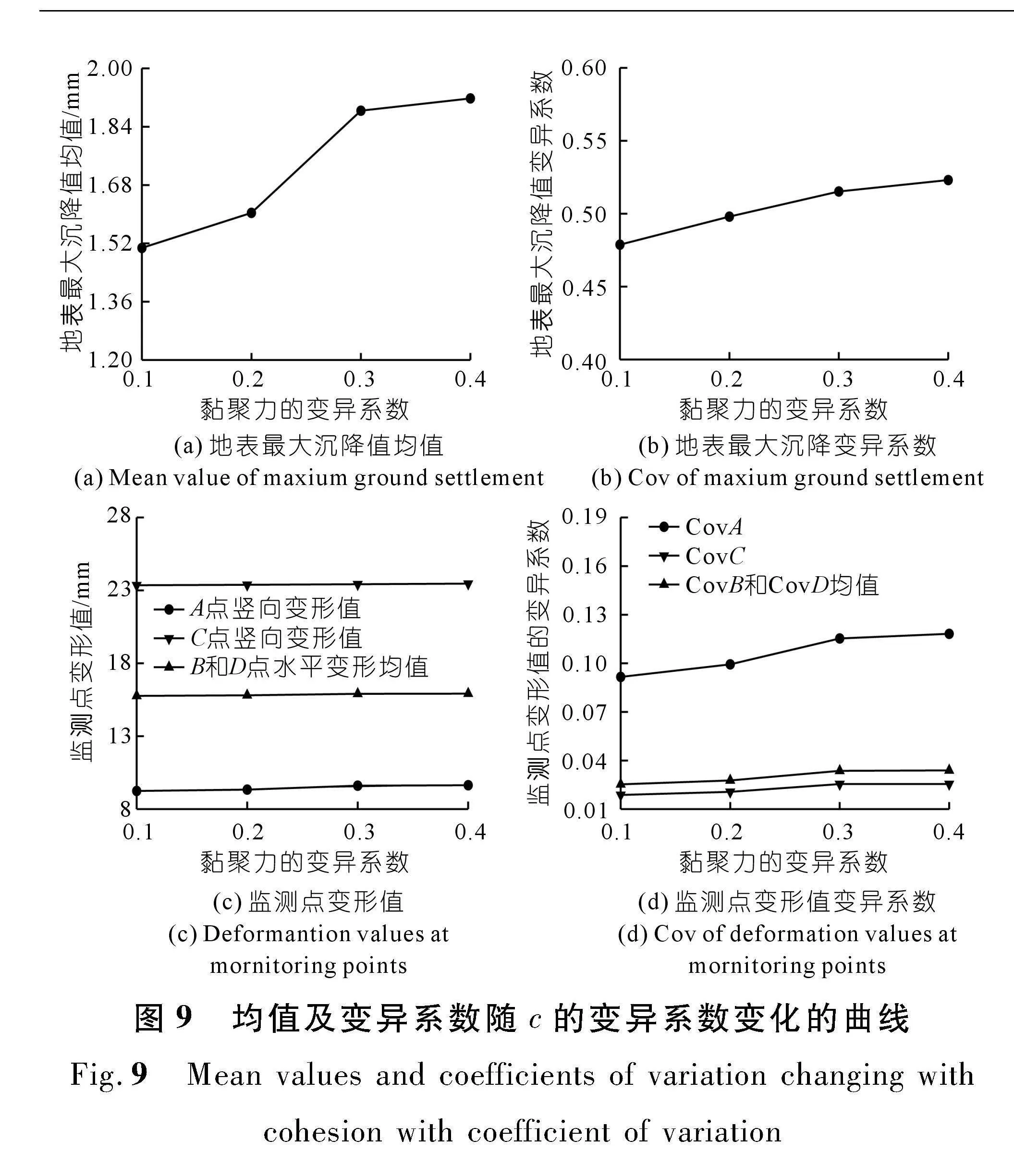
由图9（a）可知，工况ISO-25到ISO-28，地表最大沉降值均值从1.507 mm增加到1.918 mm，增加了27.27%。整体变化较大，特别是当c的变异系数从0.2增加到0.3时，地表最大沉降值均值出现了明显增长，说明当c的变异系数达到某一个特定的范围时，地表沉降变形会发生较大变化。因此在实际工程中应通过模拟计算找出这一特定范围，才能更好地进行隧道支护与设计。由图9（b）可知随着变异系数逐渐增大，地表最大沉降值的变异系数从0.478 8增加到0.523 1，增加了9.25%。可见最大地表沉降值的分布随c的变异系数在0.1～0.4逐渐增加时也逐渐离散。综合上述分析，地表沉降变形随着c的变异系数和相关距离的变化呈现出不同的变形程度，其对Cov c的变化更为敏感。

由图9（c）和（d）可知，当Cov c在0.1～0.4变化时对隧道变形均值的影响很小，综合上述分析可知Covc的空间变异性对各监测点变形值均值影响较小。然而各监测点变形值的变异系数出现了明显的变化，特别当Cov c从0.2增加到0.3时，其监测点变形值变异系数出现了明显的增长，Cov A从0.091 6增加到0.118 2，Cov C从0.018 8增加到0.025 5，Cov B和Cov D从0.025 4增加到0.033 9，增长百分比分别为29.04%，35.64%，33.46%。数据表明黏聚力c的变异系数对隧道变形有着重要的影响，在实际工程中要更加注重Cov c的测算工作。

3" 考虑内摩擦角空间变异性的地表和隧道变形分析

3.1" 内摩擦角不同相关距离

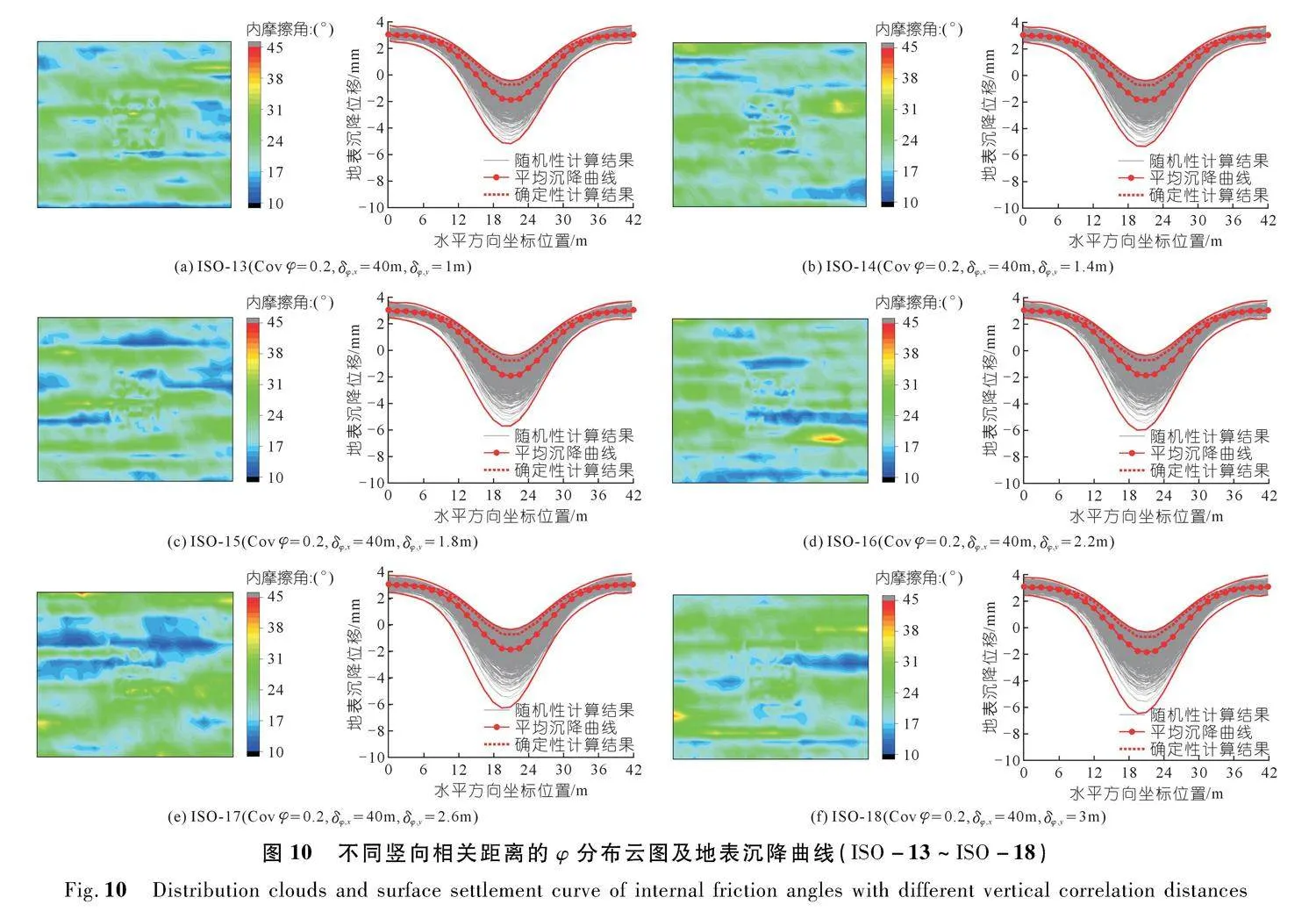
图10为ISO-13到ISO-18的参数分布云图以及地表沉降曲线。地表平均沉降曲线比确定性分析结果表现出了更大的沉降，由此可知不考虑φ的竖直相关距离将偏小地预测地表变形。随着φ的竖直相关距离在1～3 m逐渐增大，地表沉降曲线簇的波动范围也出现了一定的增大，尽管这一变化并不明显。

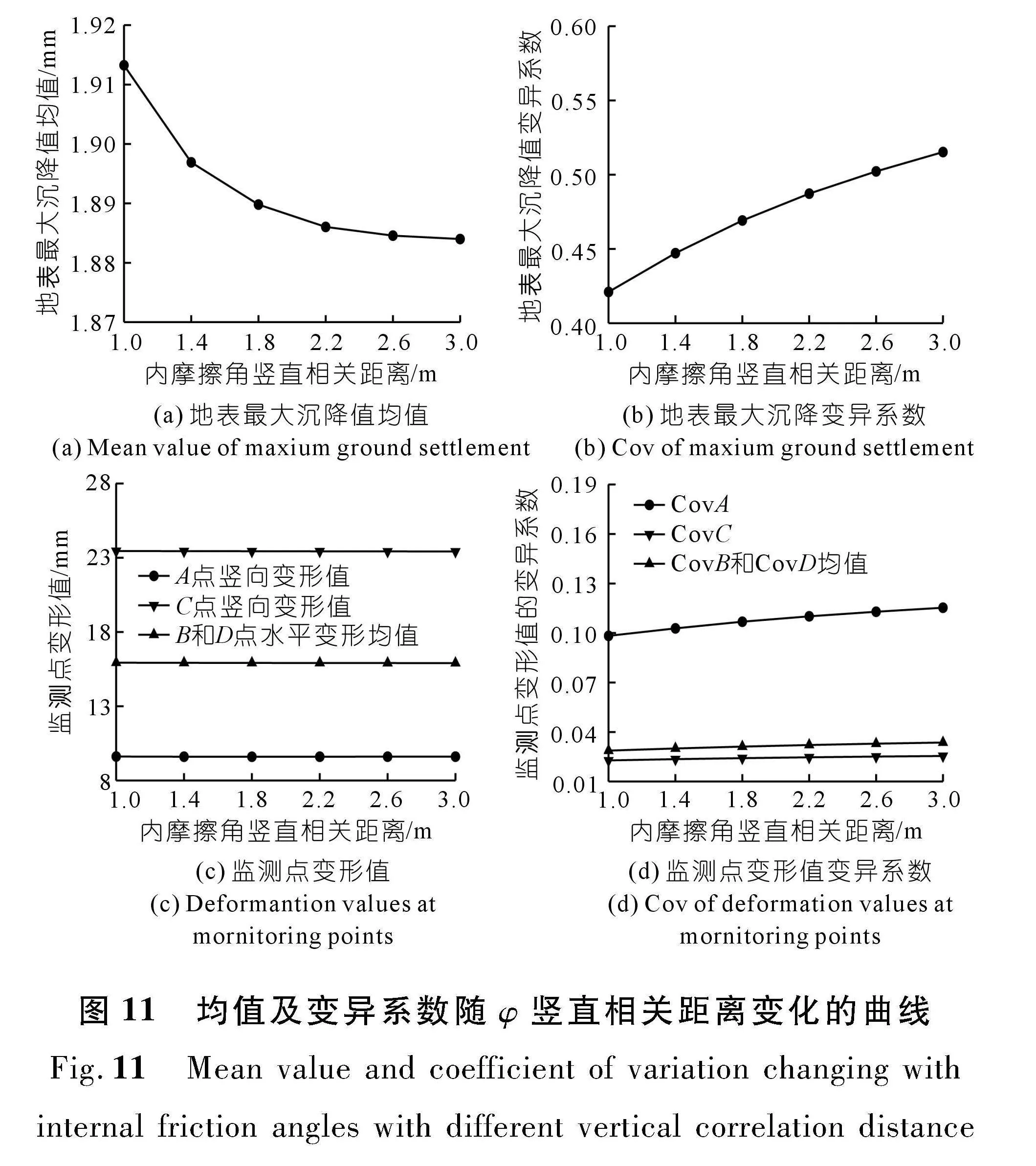
由图11（a）可知，ISO-13到ISO-18，地表最大沉降均值随着φ竖直相关距离在1～3 m增大时，地表最大沉降值从1.913 mm下降到1.884 mm，下降了1.51%。然而在其竖直相关距离大于2.2 m后均值没有出现明显的变化，这表明φ的竖直相关距离对其均值的影响有限。由图11（b）可知，随着φ的竖直相关距离逐渐增大，地表最大沉降值变异系数从0.421 0增加到了0.515 2，增加百分比为22.37%。上述分析表明，地表最大沉降值的分布随着φ和c的竖直相关距离的增大而逐渐离散，但φ的竖直相关距离对地表最大沉降值的分布影响更大。

由图11（c）和（d）可知，φ的竖直相关距离在1～3 m变化时，隧道各监测点变形均值没有出现明显的变化。其监测点B、C、D的变形值的变异系数也没有出现明显的波动。然而A点变形值变异系数从0.098 3增加到0.115 3，增加了17.30%，出现了更明显的增长，因此在实际隧道施工时对拱顶的监测应更加密切，及时做好数据记录工作。

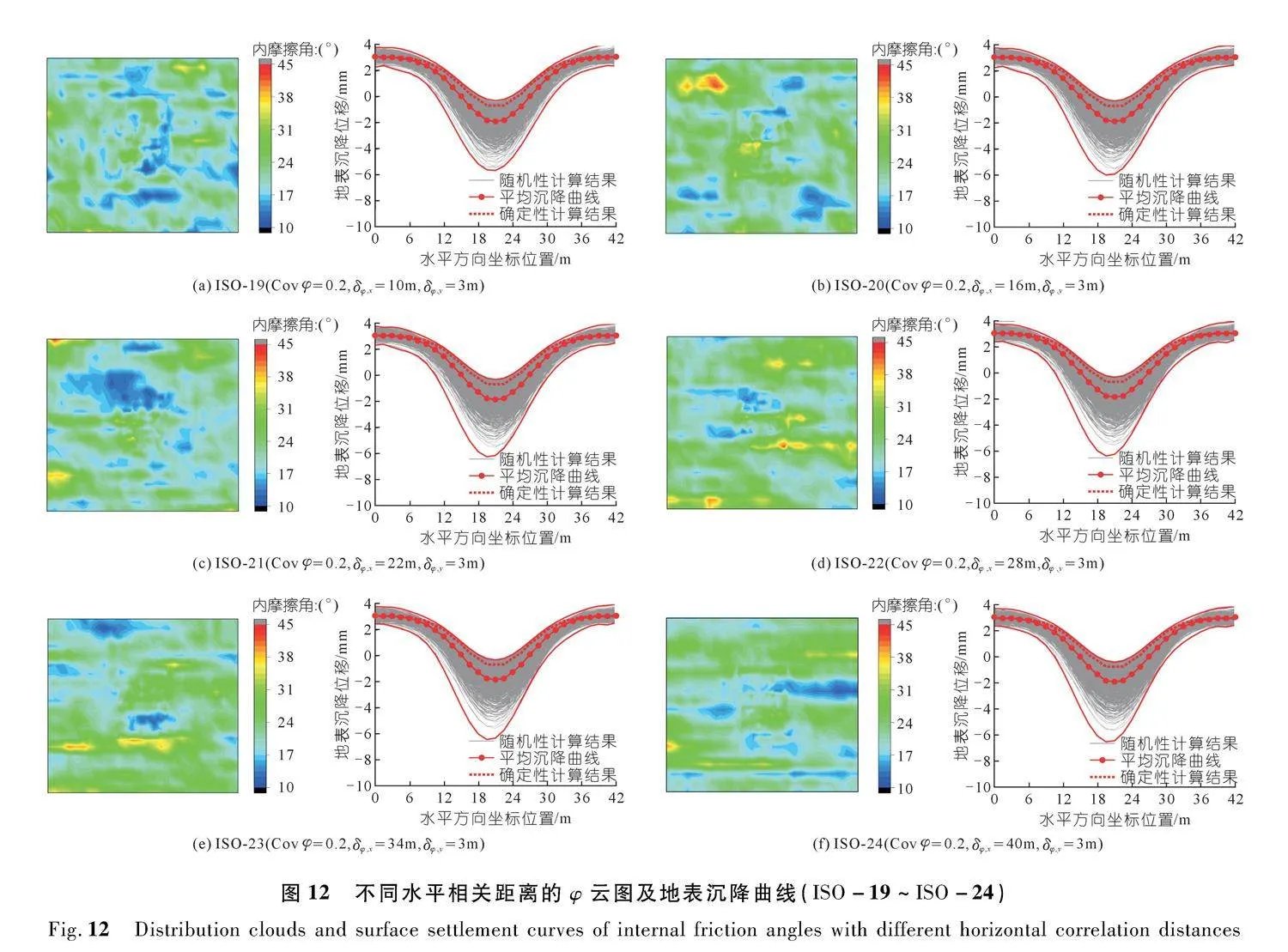
图12为ISO-19到ISO-24的参数分布云图以及地表沉降曲线。从图中可知，地表平均沉降曲线比确定性分析结果表现出了更大的沉降，此外随着φ的相关距离逐渐增大，地面沉降曲线簇的分布逐渐离散。上述分析表明，φ的相关距离变化对地表沉降变形的影响要强于c的相关距离变化对地表沉降变形的影响。

由内摩擦角的分布云图可知，随着相关距离的增大，参数云图也同样呈现出不同程度的变化。当φ的竖直相关距离在1～3 m逐渐增大时其参数的竖向相

关性逐渐增大，但是云图变化不明显，这跟其竖直相关距离波动范围较小有关。然而当φ的水平相关距离在10～40 m逐渐增大时，可以明显从云图看出参数水平向的连贯性及相关性有明显的提升。

跟前文的地表沉降曲线对比可知，由于其土体参数本身具有的空间变异性，多次随机模拟得到的地表沉降曲线簇的波动范围各有不同，但地表沉降曲线的形态无显著差异都符合正态分布曲线。结果表明，当土体参数相关距离越大，地表下沉曲线的包络线变化幅度越大。这是因为，在较小的相关距离下，低强度区分布的空间较少，不能构成完整的滑移面，但在较大的相关距离下，会出现大面积低强度区，进而引起较大的变形。

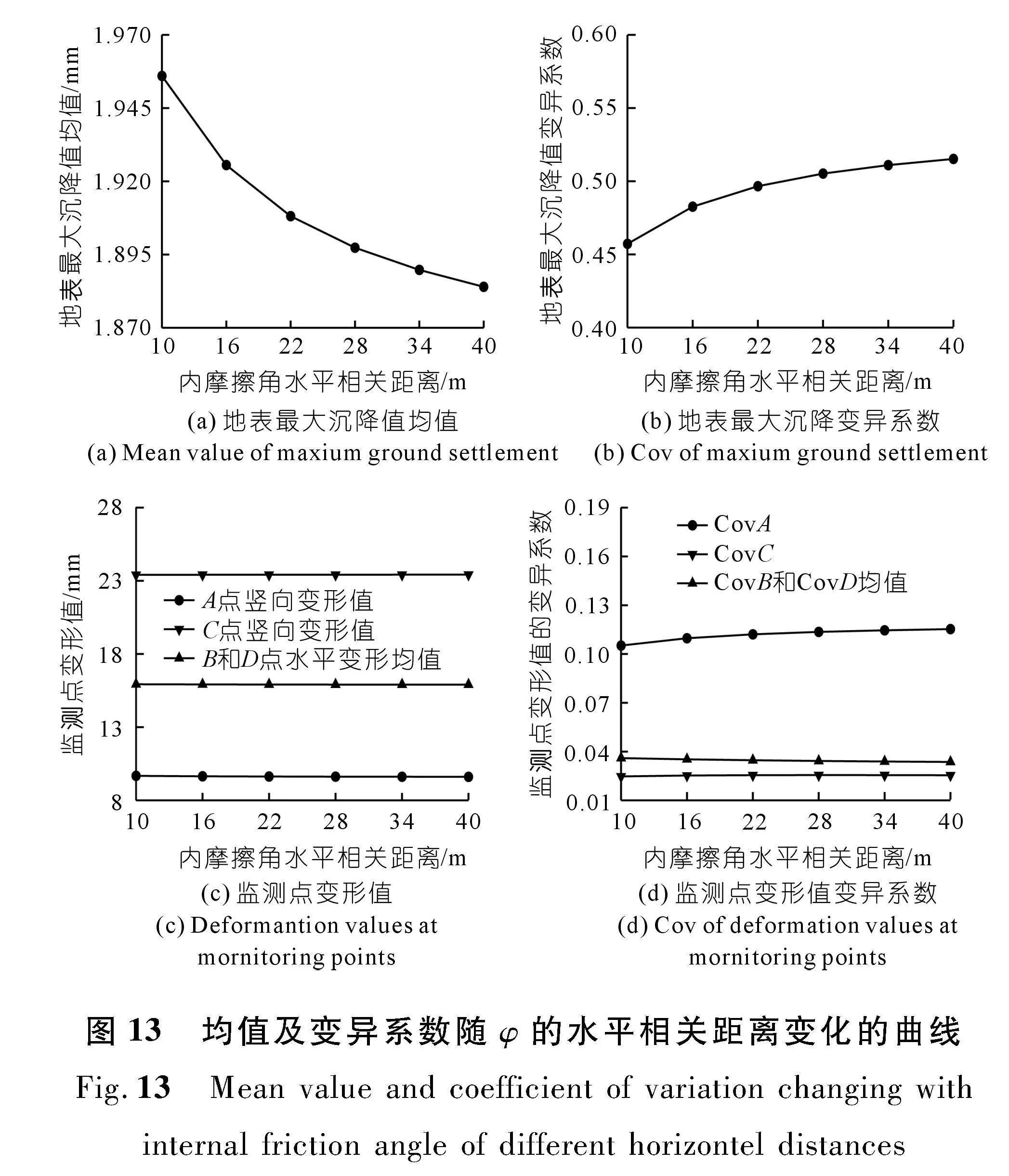
由图13（a）可知，ISO-19到ISO-24，各工况地表最大沉降值均值从1.956 mm下降到1.884 mm，下降了3.68%。当φ水平相关距离在10～40 m逐渐增大时其地表最大沉降值均值出现了较大幅度的下降。由图13（b）可知随着φ的水平相关距离逐渐增大，地表最大沉降值的变异系数从0.457 2增加到0.515 3，增加了12.71%，整体出现明显增长，但在相关距离大于28 m后变异系数逐渐稳定，说明φ的水平相关距离对地表最大沉降值分布影响有限，当变异系数达到某一阈值后逐渐稳定。

由图13（c）和（d），可知内摩擦角φ水平相关距离在10～40 m变化时对隧道变形均值的影响依然很小。其监测点B、C、D的变形值的变异系数也没有出现明显的波动。然而A点其变形值变异系数从0.105 2增加到0.115 3，增加了9.60%，出现了更明显的增长，因此在实际隧道施工时对拱顶的监测应更加密切。通过前文对比可知，隧道监测点A的变形值分布随着φ的相关距离的增大而逐渐离散，而φ的竖直相关距离对其变形值的影响更大。

3.2" 内摩擦角变异系数

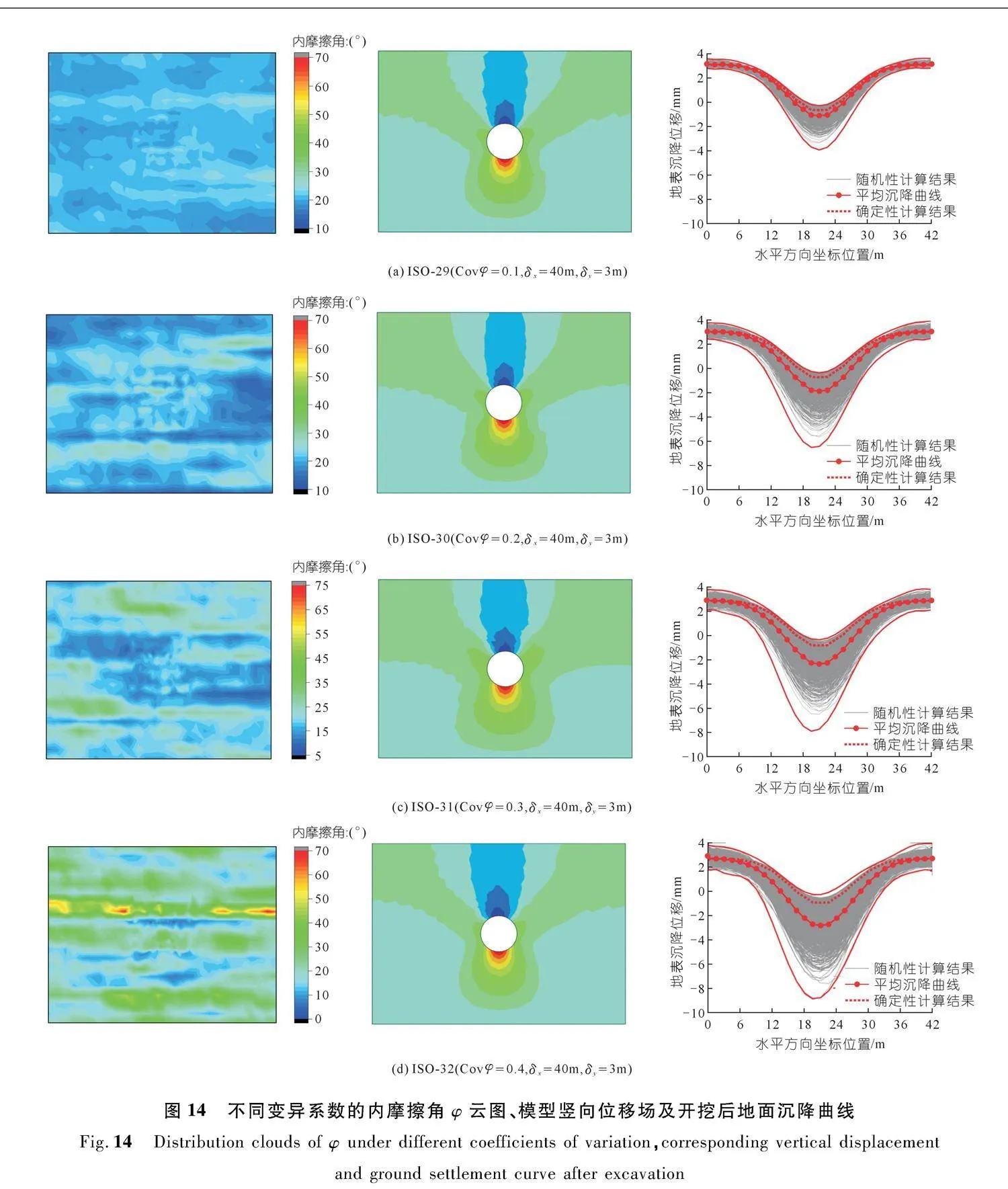
内摩擦角φ变异系数Cov φ分别取为0.1，0.2，0.3，0.4。对于每个Cov φ值，均采用乔列斯基分解中点法。随机模拟1 000次作为一组算例。图14为内摩擦角φ分布云图、模型竖向位移场及开挖后地面沉降曲线。可以发现每一次生成参数的随机场不同，地面沉降曲线簇的波动范围也有所差异，但仍然符合正态分布曲线。

由图14的内摩擦角φ云图可知，当Cov φ从0.1增加到0.4时，φ的数值波动范围出现了明显的增大，与此同时随着Cov φ的增大，其竖向位移场逐渐呈现明显的不对称性，即宏观表现为地表沉降曲线的不对称性。综上所述，由不同土体参数变异系数得到的沉降曲线可知，随着变异系数的增大，土体参数的不均匀性逐渐增加，地面沉降曲线簇分布逐渐离散。当Cov φ=0.1时随机模拟得到的地面沉降曲线更加集中于确定性计算结果附近，综合前文分析可知，Cov φ对沉降曲线的影响最为明显。具体而言，土体内摩擦角的变异程度越大，对地表沉降曲线的影响越大。所以在实际的勘察以及设计环节，要更加注意施工区域内φ的测算工作。

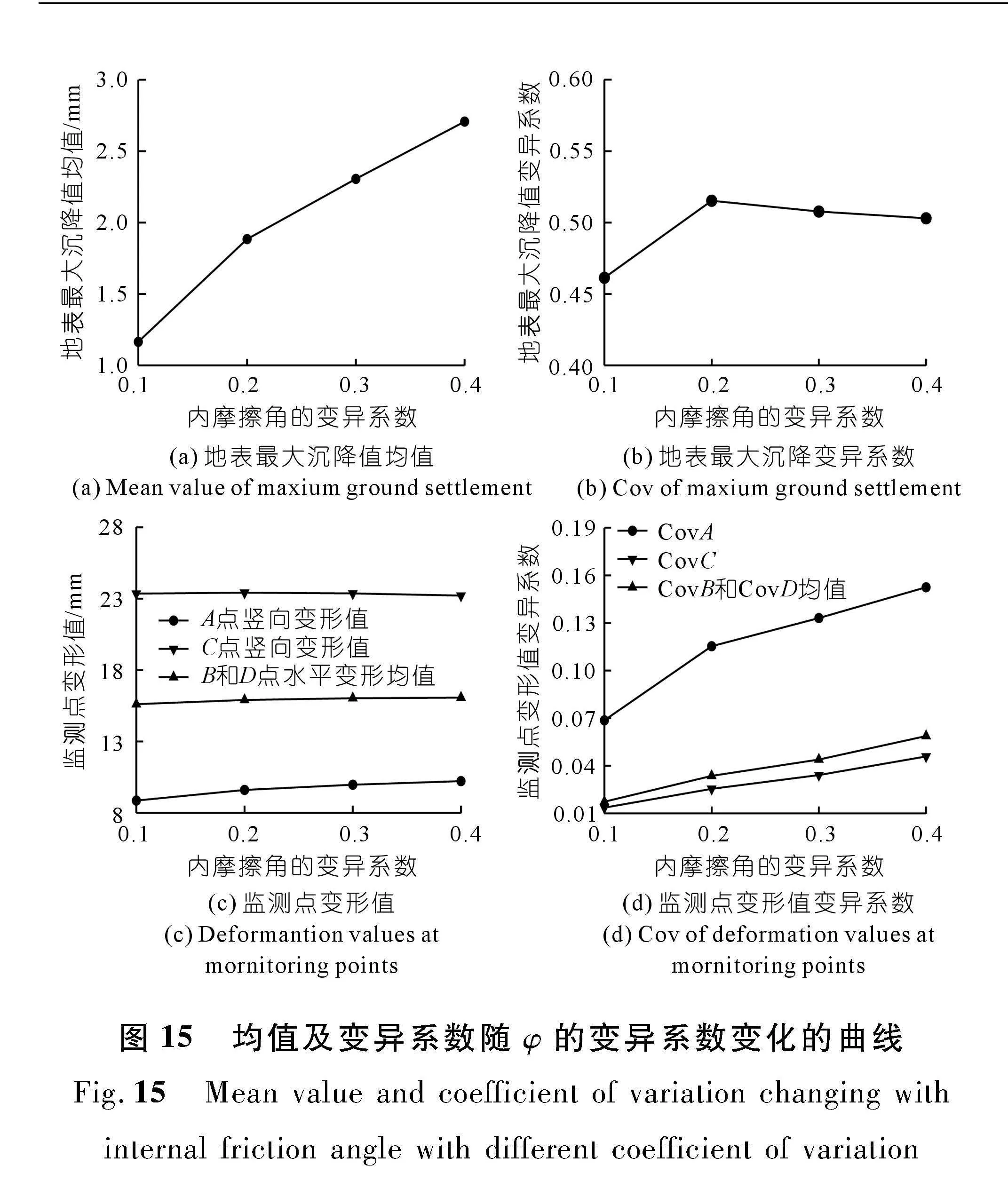
由图15（a）可知，ISO-29到ISO-32，最大沉降值均值从1.165 mm增加到2.707 mm，增大了2.32倍，

整体变化很大。可以看出，Cov φ对地表最大沉降值的均值影响很大。由图15（b）可知随着Cov φ在0.1～0.4变化时地表最大沉降值变异系数从0.461 3增加到0.503 0，增大了9.03%。但图15（b）中的曲线是呈现先上升然后出现缓慢回落，说明当Cov φ达到某一定值时，地表最大沉降值的变异系数也达到一个阈值。

由图15（c）和（d）可知，Cov φ在0.1～0.4变化时，其监测点B、C、D的变形值均值没有出现明显的变化，然而A点其变形值的均值出现了缓慢增长。与此同时它们各点变形值的变异系数出现明显的增大，Cov A从0.068 7增加到0.152 5，Cov C从0.013 6增加到0.045 9，Cov B和Cov D的均值也从0.017 4增加到0.058 8，增长百分比分别为121.80%、237.5%、237.94%。可见变异系数过大将提高隧道变形的风险。上述综合分析表明，相比于c和φ的相关距离对隧道变形的影响，它们的变异系数对隧道变形有着更重要的影响，尤其是Cov φ的变化对隧道变形的影响最为显著。

4" 结 论

本文利用随机有限元模型分析黏聚力和内摩擦角的空间变异性对隧道开挖的地表变形及隧道变形的影响，得到的主要结论如下：

（1） 地表沉降曲线簇的波动范围分别随着黏聚力和内摩擦角相关距离的增大而逐渐增大。相比水平相关距离，它们的竖直相关距离的变化对地表沉降变形的影响更大，尤其是内摩擦角竖直相关距离对地表变形的影响更突出。

（2） 随着黏聚力和内摩擦角的变异系数的增大，地表沉降曲线簇的分布逐渐离散。但内摩擦角的变异系数对地表变形的影响强于其相关距离对地表变形的影响。

（3） 黏聚力和内摩擦角的相关距离和变异系数变化对隧道收敛变形的均值影响较小，而对隧道拱顶变形值的变异系数影响较为明显。特别是黏聚力和内摩擦角的变异系数的变化对4个控制点变形值的变异系数影响更大。

（4） 在实际隧道支护设计时，如果不考虑黏聚力和内摩擦角的空间变异性将偏小地预测地表沉降和隧道变形，使设计偏于危险。

参考文献：

［1］" 贾宇峰，葛培杰，相彪，等.红石岩堰塞坝力学参数随机场模拟研究［J］.人民长江，2022，53（8）：173-178.

［2］" 蒋水华，刘贤，黄发明，等.考虑多参数空间变异性的降雨入渗边坡失稳机理及可靠度分析［J］.岩土工程学报，2020，42（5）：900-907.

［3］" HING J，HU Y G，PHOON K K.Effective Young′s modulus of a spatially variable soil mass under a footing［J］.Structural Safety，2018，73：99-113.

［4］" LUO Z，LI Y X，ZHOU S H，et al.Effects of vertical spatial variability on supported excavations in sands considering multiple geotechnical and structural failure modes［J］.Computers and Geotechnics，2018，95：16-29.

［5］" VANMARCKE E H.Probabilistic modeling of soil profiles［J］.Journal of the Geotechnical Engineering Division，1977，103（11）：1227-1246.

［6］" 张隆松，李典庆，曹子君，等.考虑统计不确定性的基坑变形可靠度高效蒙特卡洛分析方法［J］.武汉大学学报（工学版），2019，52（3）：207-215.

［7］" 易顺，林伟宁，陈健，等.基于随机场理论的基坑开挖地表及围护墙变形分析［J］.岩石力学与工程学报，2021，40（增2）：3389-3398.

［8］" 王曙光，夏鹏，董潇阳，等.考虑空间变异性的地基极限承载能力上限有限元分析［J］.中外公路，2021，41（4）：27-31.

［9］" 盛建龙，杨博，翟明洋.随机场模型下相关距离及参数变异系数对边坡稳定可靠度的影响［J］.金属矿山，2018，510（12）：157-162.

［10］GRIFFITHS D V，HUANG J S，FENTON G A.Influence of spatial variability on slope reliability using 2-D random fields［J］.Journal of Geotechnical and Geoenvironmental Engineering，2009，135（10）：1367-1378.

［11］CHENG H Z，CHEN J，CHEN R P，et al.Risk assessment of slope failure considering the variability in soil properties［J］.Computers and Geotechnics，2018，103：61-72.

［12］程红战，陈健，王占盛，等.考虑旋转各向异性相关结构的黏土边坡稳定性分析［J］.岩石力学与工程学报，2017，36（增2）：3965-3973.

［13］程勇刚，常晓林，李典庆.考虑岩体空间变异性的隧洞围岩变形随机分析［J］.岩石力学与工程学报，2012，31（增1）：2767-2775.

［14］陈扬，袁宗义，梁禹.考虑土体空间变异性的管廊基坑开挖过程中变形及能量演化特征分析［J］.科学技术与工程，2022，22（17）：7127-7134.

［15］张东明，李保军，张琳，等.复合地层中空间变异性对大直径隧道变形性能的影响［C］∥世界交通运输工程技术论坛论文集（下），2021.

［16］靳雪梅，黄宏伟，张东明.关于土的空间变异性对盾构隧道施工影响的探讨［J］.现代隧道技术，2022，59（2）：62-70.

［17］蒋水华，李典庆，周创兵，等.考虑自相关函数影响的边坡可靠度分析［J］.岩土工程学报，2014，36（3）：508-518.

（编辑：郑 毅）

Analysis on surface and tunnel deformation after tunnel excavation based on random field theory

WANG Qin，YAN Long，ZHANG Haiying，LIU Lijiao，LIU Yanjie

（College of Civil Engineering，Heilongjiang University，Harbin 150080，China）

Abstract：

Natural soil has inherent uncertainties due to the influence of multiple factors.In order to better reflect the distribution of actual soil parameters，a combination of Cholesky decomposition and stochastic finite element model was utilized to analyze the surface and tunnel deformation based on random field theory，in which the spatial variability of cohesion and internal friction angle were taken into account.The results indicated that the fluctuation range of the surface settlement curves cluster expanded with the increasing of related distance of cohesion and internal friction angle，and the effect of vertical related distance on surface settlement deformation was more significant.Furthermore，the influence of the cohesion variation coefficient and internal friction angle on surface settlement deformation was stronger than the effect of related distance.In addition，the distribution of the tunnel deformation values scattered with the increasing of the coefficient of variation of cohesion and internal friction angle，in which the coefficient of variation of internal friction had much influences.Neglecting the spatial variability of cohesion and internal friction angle could result in underestimating the predicted surface settlement and tunnel deformation，making the design more risky.

Key words：

tunnel excavation； ground surface settlement curve； random field； spatial variability； correlation distance； stochastic finite element model