基于等效理论的水下双孔隧道渗流场半解析研究

摘要：

为研究隧道设计参数对水下双孔隧道渗流场的影响，建立了水下双孔平行隧道渗流计算模型。运用Abaqus软件构建数值模型，以隧道埋深、双孔间距和支护结构参数为影响因素，分析各因素对解析解计算误差的影响以及支护结构外水压力的变化特征，并采用灰色关联理论研究各影响因素的敏感度。最后，基于数值计算结果对解析解进行修正，得到计算精度较高的半解析解。结果表明：二次衬砌结构参数对初期支护外水压力的折减幅度影响较大，埋深、间距和注浆圈参数对初期支护外水压力的折减幅度影响较小。支护结构渗透系数对拱顶处解析解计算误差影响较大，支护结构厚度对拱底处解析解计算误差影响较大。埋深与等效半径之比小于19时，解析解计算误差大致为12%。注浆圈渗透系数与二次衬砌渗透系数之比小于20时，拱顶处解析解计算误差超过10%。注浆圈渗透系数对拱顶处解析解计算误差影响较大，隧道埋深对拱底处解析解计算误差影响较大。

关" 键" 词：

水下双孔隧道； 渗流； 半解析解； 灰色关联分析； 外水压力

中图法分类号： U452.11

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.07.027

收稿日期：

2023-06-04

；接受日期：

2023-10-18

基金项目：

福建省中青年教师教育科研项目（JT180256）；福建省自然科学基金青年创新项目（2020J05145）

作者简介：

潘以恒，男，讲师，博士，从事岩土与地下工程研究。E-mail： panyihengok@163.com

通信作者：

陈" 超，男，讲师，博士，从事港口、海岸与近海工程研究。E-mail： chenchaojmu@126.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 07-0204-08

引用本文：

潘以恒，罗其奇，阮彩添，等.基于等效理论的水下双孔隧道渗流场半解析研究

［J］.人民长江，2024，55（7）：204-211.

0" 引 言

随着水利水电技术的发展，水工隧洞被广泛用作输水和泄洪等的通道［1］。水工隧洞的支护结构所受外水压力一直是重要的设计参数［2］，也对水工隧洞工程稳定性影响较大［3］。采用解析法进行受外水作用的隧道渗流场计算具有高效、准确性高等优点。Goodman［4］等推导出半无限各向同性介质中的隧道渗流场镜像法解析解。El Tani［5］推导出半无限各向同性介质中单孔圆形隧道渗流场解析解。张丙强［6］将镜像法运用到双孔圆形隧道渗流场计算中，推导了双孔平行隧道镜像法解析解。王帅等［7］在半无限各向同性介质中推导了三孔平行水下圆形隧道渗流场解析解，同时研究了隧道间距、初期支护厚度和注浆圈厚度对隧道渗流场的影响。应宏伟等［8］推导了考虑注浆圈及衬砌作用的半无限渗流场镜像法解析解。乔彤等［9］考虑了隧道周围介质各向渗透异性对隧道渗流场的影响，通过保角变换等方法推导出不规则单孔隧道渗流场解析解，并通过数值计算验证了解析解的适用性。

以上隧道渗流场解析解大多适用于单孔隧道，尚缺乏多孔不规则隧道的渗流场解析解。已有不规则隧道渗流场解析解考虑因素不够全面，不能同时考虑初期支护、二次衬砌和注浆圈的作用［10-11］。对于不规则隧道的处理方法，一般采用等效周长法或等效面积法转化为圆形规则隧道进行简化计算［12-13］。

本文选取双孔四心圆不规则水下隧道，提出基于等效理论的水下隧道渗流场简化解析解，同时研究隧道埋深、间距和支护参数对简化解析解与数值解计算误差的影响规律，并依据解析解计算误差对简化解析解进行修正。研究成果可用于外水压力作用下的水工隧洞渗流场解析计算，可为水工隧洞建设提供理论参考依据。

1" 水下双孔隧道渗流场解析解

1.1" 计算模型与解析解

半无限平面水下双孔平行圆形隧道模型如图1所示。假设围岩、注浆圈和衬砌均为均匀、各向同性介质，渗流符合达西定律，隧道衬砌内部水头为0。

针对双孔隧道渗流场解析问题，已有研究均采用镜像法与叠加原理进行求解［6-7］，过程如下：① 基于拉普拉斯方程和达西定律，推导出单孔隧道渗流场的水头函数。② 采用镜像法分析，与等势面对称位置映射为虚拟隧道，将图1所示的双孔平行隧道转化为如图2所示的4孔隧道渗流场，边界条件是渗流量等量异号。③ 根据叠加原理，无限平面中双孔隧道渗流时水头可叠加，未知参数根据边界条件确定。

根据达西定律，流速v和渗透系数k与水力梯度J之间满足如下关系：

J=vk

（1）

根据流速与水力梯度的定义：

dhdρ=Q2πρk

（2）

式中：h为总水头，ρ为渗流半径，Q为流量。

对式（2）积分可得单孔隧道渗流场内任意一点的水头函数如下：

h=Q2πklnρ+C

（3）

根据叠加原理，双孔平行隧道渗流场内任意一点的水头函数为

h=Q2πklnρ1ρ2+C0

（4）

式中：C0为待定系数。

文献［6～7］根据隧道断面流量相等原则，给出了双孔隧道埋深和半径相等时，不含位置水头的初期支护和二次衬砌外水压力解析解如式（5）、（6）所示。该式均未考虑位置水头对解析解计算误差的影响，本文针对不含位置水头的解析解开展计算误差分析，以此提出更方便、计算精度更高的半解析解。

Pc=krkllnrlr+krkclnrcrl×Hln2db2+d2brg+krkglnrgrc+krkclnrcrl+krkllnrlr×γw

（5）

Pl=krkllnrlr×Hln2db2+d2brg+krkglnrgrc+krkclnrcrl+krkllnrlr×γw

（6）

式中：kr，kg，kc，kl分别为围岩渗透系数、注浆圈渗透系数、初期支护渗透系数、二次衬砌渗透系数，Pc与Pl分别为初期支护与二次衬砌外水压力。

1.2" 等效周长理论

上述解析解均只适用于规则的圆形隧道，目前对于多孔不规则隧道渗流场解析问题，大多采用等效原理进行简化计算［14］。

对于不规则隧道断面需要采用等效公式转化为规则断面，采用等效周长法简化计算，公式如下：

r=l2π（7）

式中：l为不规则隧道的周长；r为通过等效周长法换算得到的对应规则圆形隧道的半径。

2" 渗流场解析解计算误差分析

2.1" 数值模型

采用Abaqus有限元软件建立二维四心圆断面隧道流固耦合计算模型，围岩的渗透系数为2×10-6 m/s，初期支护、二次衬砌和注浆圈的初始渗透系数分别为1×10-8，1×10-9，2×10-7 m/s。初期支护、二次衬砌和注浆圈的初始厚度分别为0.2，0.5，5 m，数值计算模型的材料参数如表1所列。四心圆断面隧道初始开挖尺寸如图3所示，数值计算模型如图4所示。数值模型宽度和深度分别为200，150 m，地表水头高度为15 m，模型中二次衬砌内水头为0。

2.2" 计算方案

为了明晰不同隧道施工参数对支护结构外水压力解析解计算误差的影响，并探究隧道埋深、双孔间距以及支护参数对支护结构外水压力的影响，本文采用6种计算方案进行对比分析。方案1：隧道埋深分别取35，55，75，95，115 m；方案2：双孔隧道间距分别取20，25，30，35，40 m；方案3：隧道注浆圈厚度分别取1，3，5，7，9 m；方案4：隧道二次衬砌厚度分别取0.2，0.35，0.5，0.65，0.8 m；方案5：隧道注浆圈渗透系数分别取0.1×10-7，0.2×10-7，0.4×10-7，1×10-7，2×10-7 m/s；方案6：隧道二次衬砌渗透系数分别取0.5×10-9，1×10-9，2×10-9，4×10-9，10×10-9 m/s。对以上6种计算方案，分别求取衬砌内渗流边界条件为零水头下的支护结构外水压力数值解和解析解。

2.3" 计算结果对比分析

2.3.1" 隧道埋深和间距的影响

定义解析解计算误差为ψ，计算公式如下：

ψ=PN-PAPN

（8）

式中：PN为解析解，PA为数值解。

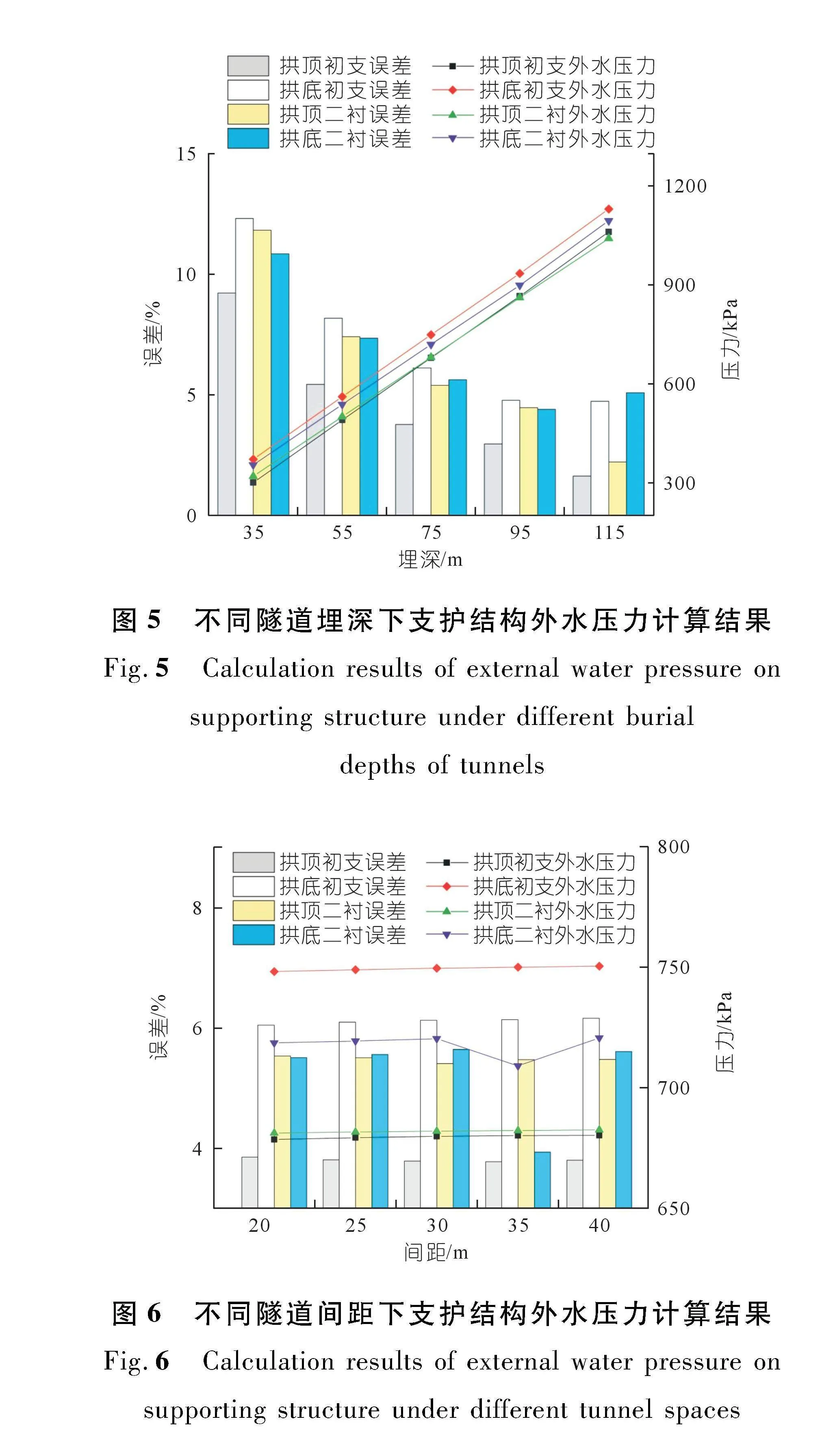
不同埋深和双孔间距下隧道支护结构外水压力对比分别如图5～6所示。由图5可知，随着隧道埋深增加，支护结构拱顶和拱底处外水压力均呈线性增加趋势。不同埋深下拱顶处初期支护结构对外水压力的折减幅度大致为4%～6.2%，拱底处的折减幅度大致为3%～4.7%。解析解计算误差随埋深整体呈降低趋势，拱顶处二次衬砌外水压力解析解计算误差较大，拱底处初期支护外水压力解析解计算误差较大。解析解计算误差随隧道埋深增加呈降低趋势，误差变化幅度逐渐减小。拱顶处外水压力解析解计算误差大致为2%～12%，拱底处计算误差大致为4%～12%。埋深与等效半径之比大于26时，计算误差均在5%以内。埋深与等效半径之比小于19时，埋深对解析解计算误差影响较大。

由图6可知，不同间距下支护结构外水压力基本保持不变，初期支护对外水压力的折减幅度均接近5%，支护结构外水压力解析解计算误差均在6%以内，间距对解析解计算误差影响较小。

2.3.2" 支护结构厚度的影响

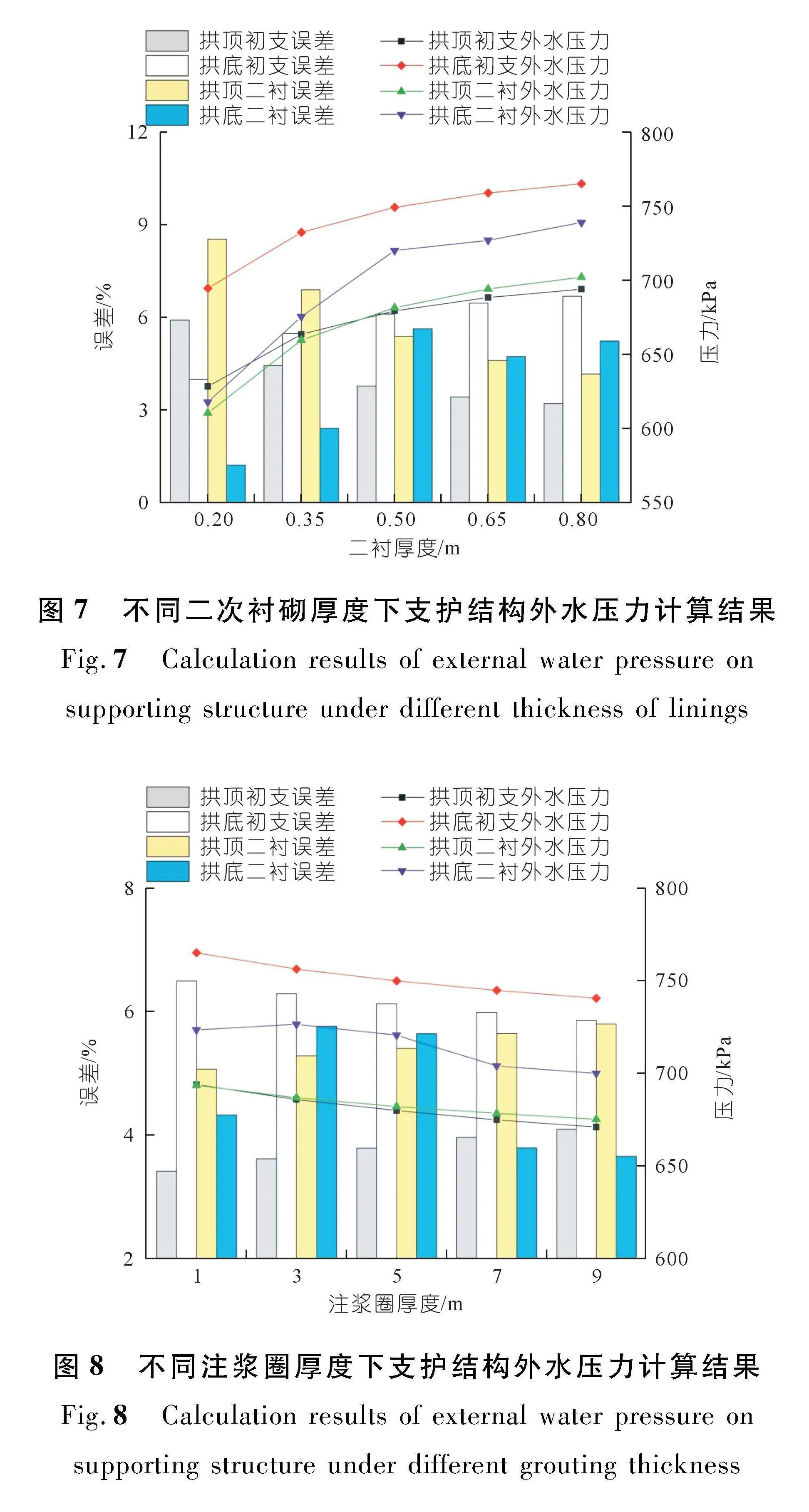
不同支护厚度下隧道支护结构外水压力对比如图7～8所示。由图7可知，随着二次衬砌厚度增加，支护结构拱顶和拱底处外水压力均呈先快速增加后缓慢增加趋势，二次衬砌外水压力变化幅度较大。初期支护对外水压力的折减幅度随二次衬砌厚度增加逐渐降低，拱顶和拱底处外水压力折减幅度大致为3%～11%。随着二次衬砌厚度增加，拱顶处解析解计算误差呈降低趋势，拱底处解析解计算误差呈增加趋势。拱顶处初期支护、二次衬砌外水压力解析解计算误差大致为3%～6%、4%～9%，拱底处计算误差大致为4%～7%、1%～5%。

由图8可知，随着注浆圈厚度增加，拱顶和拱底处支护结构外水压力呈线性降低趋势。拱顶和拱底处初期支护对外水压力的折减幅度大致为5%，注浆圈厚度对折减幅度影响较小。拱顶和拱底处解析解计算误差约为3%～7%，注浆圈厚度对解析解计算误差影响较小。

2.3.3" 支护结构渗透系数的影响

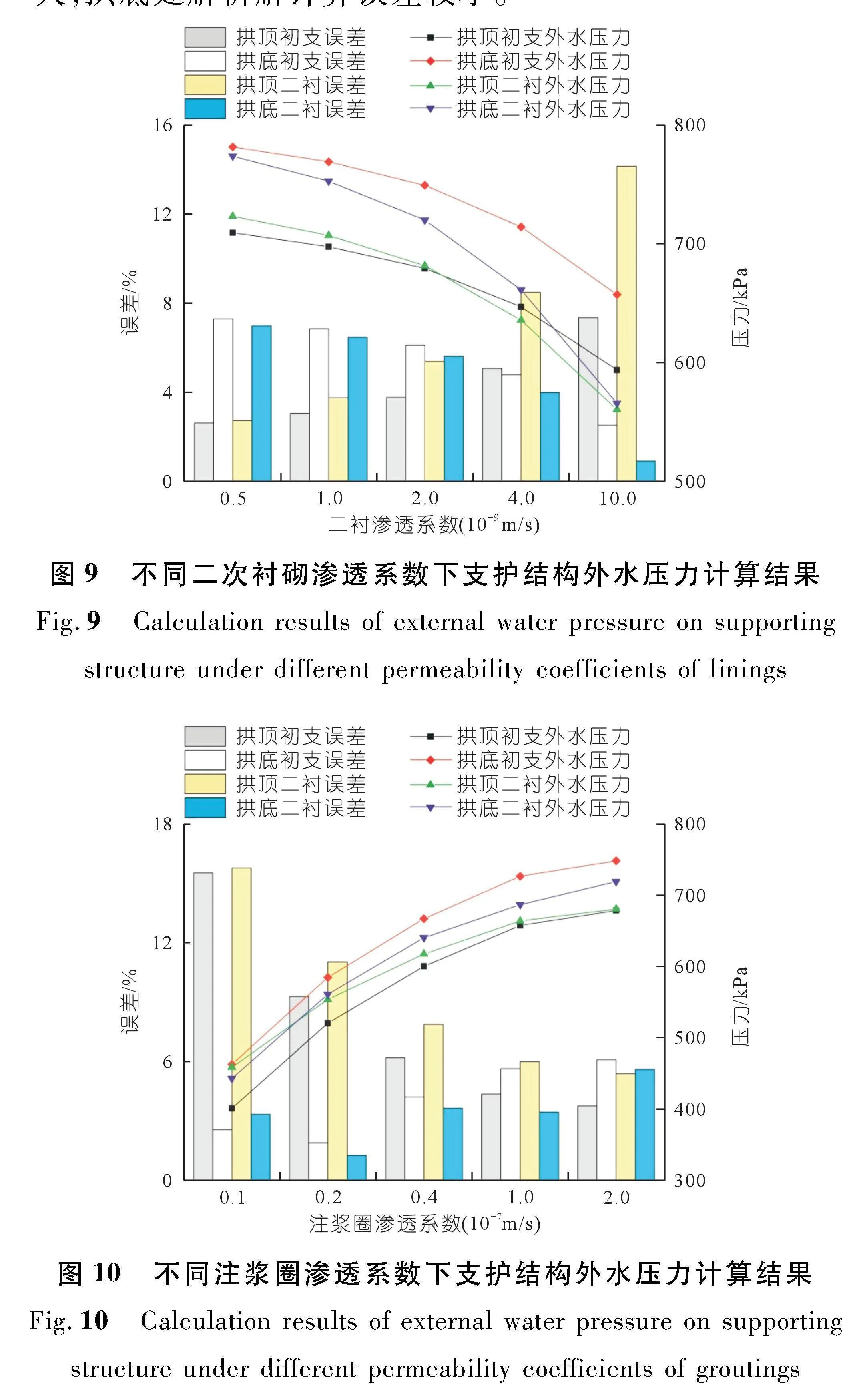
不同支护渗透系数下隧道支护结构外水压力对比分别如图9～10所示。由图9可知，随二次衬砌渗透性增强，拱顶和拱底处支护结构外水压力均呈指数降低趋势，降低幅度逐渐增大，说明增强二次衬砌渗透性可有效降低支护结构外水压力，二次衬砌渗透性对二次衬砌外水压力影响较大。拱顶和拱底处初期支护对外水压力的折减幅度随二次衬砌渗透系数增加呈指数增加的变化趋势，不同二次衬砌渗透系数下初期支护对拱顶处外水压力折减幅度较大，拱顶处初期支护对外水压力的折减幅度为1%～19%，拱底处初期支护对外水压力的折减幅度为1%～14%。随二次衬砌渗透性增强，拱顶处外水压力解析解计算误差呈增加趋势，拱底处计算误差呈降低趋势，变化幅度逐渐增加。二次衬砌渗透性对二次衬砌外水压力解析解计算误差影响较大，初期支护外水压力解析解计算误差大致为3%～7%，二次衬砌外水压力计算误差大致为1%～14%。二次衬砌与初期支护渗透系数之比高于10时，拱顶处解析解计算误差较大，拱底处解析解计算误差较小。

由图10可知，随着注浆圈渗透性增强，拱顶和拱底处外水压力呈指数增加趋势，增加幅度逐渐降低。初期支护对外水压力的折减幅度大致为5%，注浆圈渗透系数对折减幅度影响较小。随注浆圈渗透性增强，拱顶处外水压力解析解计算误差呈降低趋势，计算误差大致为4%～16%；拱底处计算误差变化幅度较小，计算误差大致为1%～6%。不同注浆圈渗透系数下，拱顶处解析解计算误差变化幅度较大。初期支护与注浆圈渗透系数之比为0.25～0.1时，拱顶处解析解计算误差较大。注浆圈渗透系数对拱底处解析解计算误差影响较小。

3" 解析解改进

3.1" 解析解计算误差影响因素关联度分析

3.1.1" 确定关联矩阵

本节研究目的是确定各因素与渗流场解析解计算误差的关联程度，从而确定各因素变化对解析解计算误差的影响程度排序［15］。选取隧道渗流场解析解与数值解计算误差的影响因素（包括埋深、间距、二次衬砌厚度、二次衬砌渗透系数、注浆圈厚度和注浆圈渗透系数）作为比较序列X，将各项参数所对应的解析解计算误差作为参考序列Y，矩阵具体形式如下：

X=x1x2xm=x11 x12…x1nx21 x22…x2n" xm1 xm2…xmn

（9）

Y=y1y2ym=y11 y12…y1ny21 y22…y2n" ym1 ym2…ymn

（10）

3.1.2" 矩阵无量纲化

由于比较序列和参考序列中的数据类型不同，各数据量纲不同，数值差异很大，为避免计算误差，需要对矩阵中各因子进行无量纲化处理。本研究采用极差变化作为无量纲化方法处理矩阵中的各因子，采用（11）～（12）式进行无量纲化处理。

x′ij=xij-minximaxxi-minxi（11）

y′ij=yij-minyimaxyi-minyi（12）

3.1.3" 灰色关联度计算

矩阵无量纲化处理之后，采用式（13）处理无量纲化矩阵中的数据，得出差序列矩阵；

μij=x′ij-y′ij

（13）

此后，采用式（14）计算关联系数矩阵中的各因子：

λij=μmin+γμmaxμij+γμmax（14）

式中：γ为分辨系数，取值范围区间为0～1，一般取为0.5。关联度取值范围为0～1，其大小反映了比较序列对参考序列的影响程度。关联度的值越接近1，说明比较序列中该影响因素的敏感性越大。各影响因素的关联度计算公式如下：

Pi=nj=1λijn（15）

式中：Pi为第i个影响因素的关联度，式（15）计算得出的关联度即为各因素的影响程度。

3.1.4" 灰色关联度分析

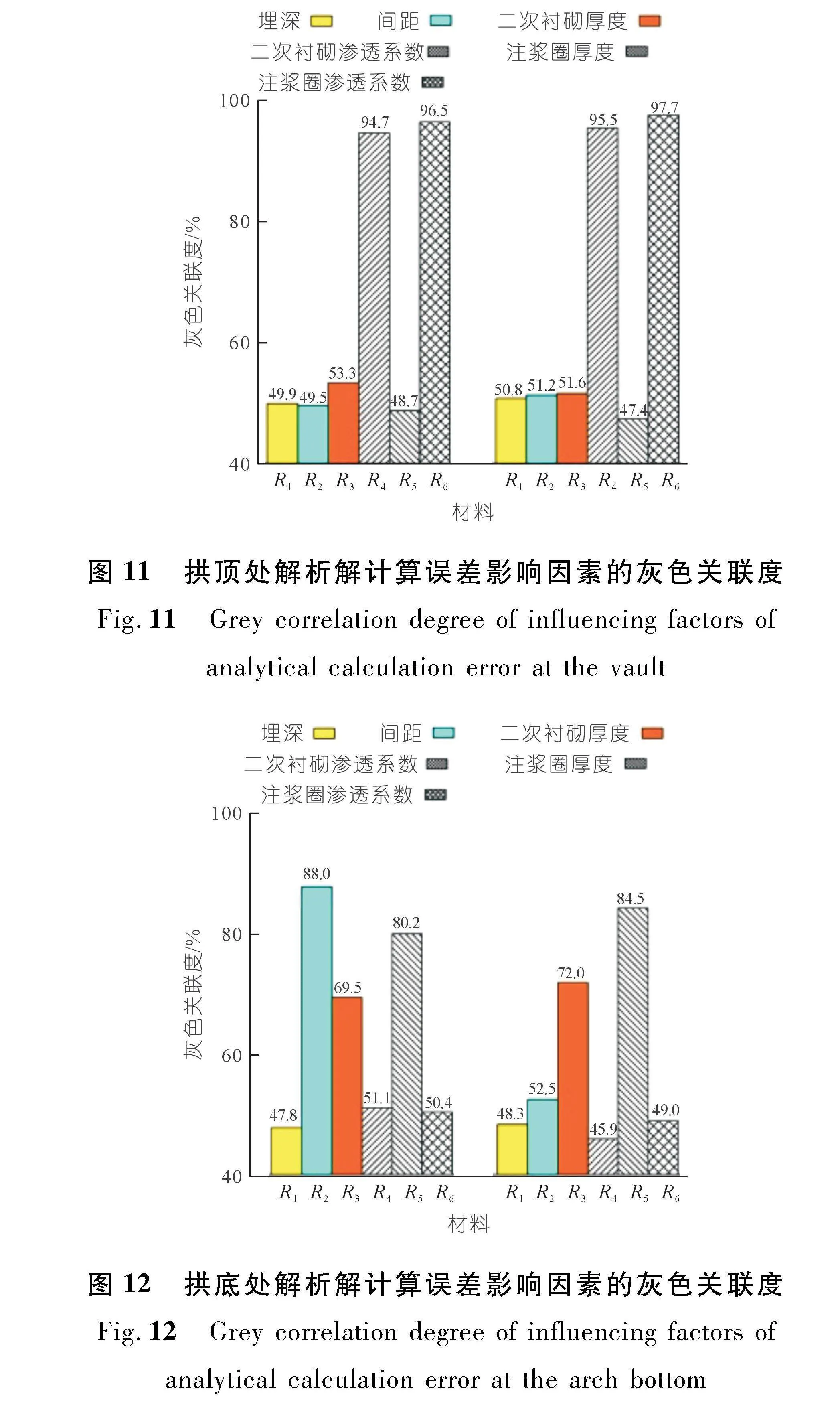
拱顶和拱底处外水压力解析解计算误差影响因素的关联度计算结果分别如图11～12所示。埋深、间距、二次衬砌厚度、二次衬砌渗透系数、注浆圈厚度、注浆圈渗透系数。

由图11可知，对拱顶处解析解计算误差影响较大的因素主要为支护结构渗透系数。拱顶处初期支护外水压力解析解计算误差的影响因素排序依次为：R6gt;R4gt;R3gt;R1gt;R2gt;R5。二次衬砌外水压力解析解计算误差的影响因素排序依次为：R6gt;R4gt;R3gt;R2gt;R1gt;R5。

由图12可知，对拱底处初期支护外水压力解析解计算误差影响较大的因素主要为间距和支护结构厚度，对拱底处二次衬砌外水压力解析解计算误差影响较大的因素主要为支护结构厚度。拱底处初期支护外水压力解析解计算误差影响因素排序为：R2gt;R5gt;R3gt;R4gt;R6gt;R1。二次衬砌外水压力解析解计算误差影响因素排序为：R5gt;R3gt;R2gt;R6gt;R1gt;R4。

3.2" 解析解的改进

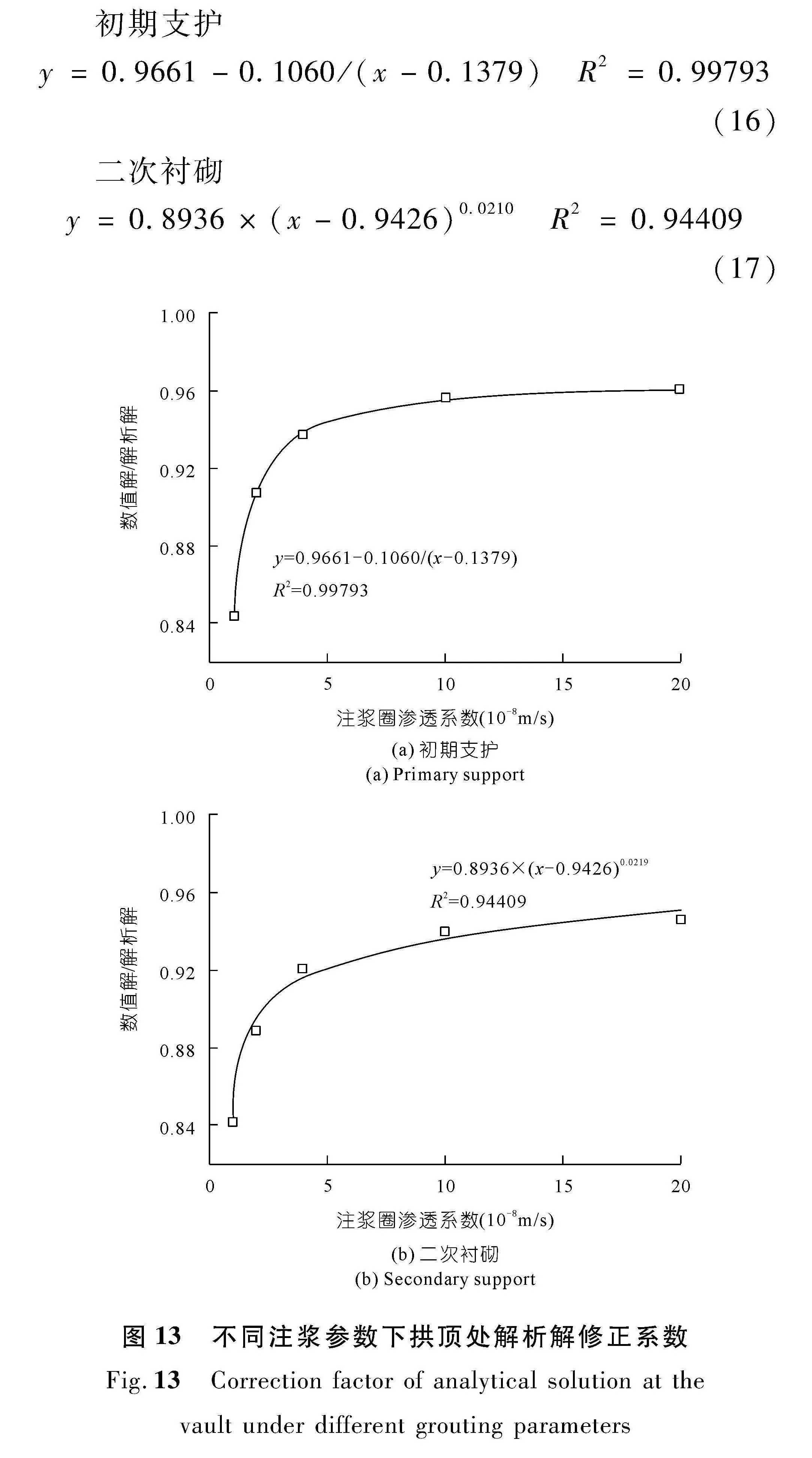
通过第2.3节分析可知，对于式（5）和（6），不同注浆圈渗透系数下拱顶处支护结构外水压力解析解计算误差最大值接近16%，为明晰解析解误差变化趋势，绘制拱顶处数值解与解析解之比在不同注浆圈渗透系数下的拟合曲线，如图13所示。由图13可知，拱顶处解析解计算结果偏大，比值随着注浆圈渗透性增强而增加，增加幅度逐渐减小，注浆圈渗透系数较小时，需改进已有解析解得到适用的半解析公式。定义数值解与解析解之比为修正系数，通过拟合得到拱顶处初期支护和二次衬砌外水压力解析解修正系数与注浆圈渗透系数的曲线方程如下：

初期支护

y=0.9661-0.1060/（x-0.1379）" R2=0.99793（16）

二次衬砌

y=0.8936×（x-0.9426）0.0210" R2=0.94409（17）

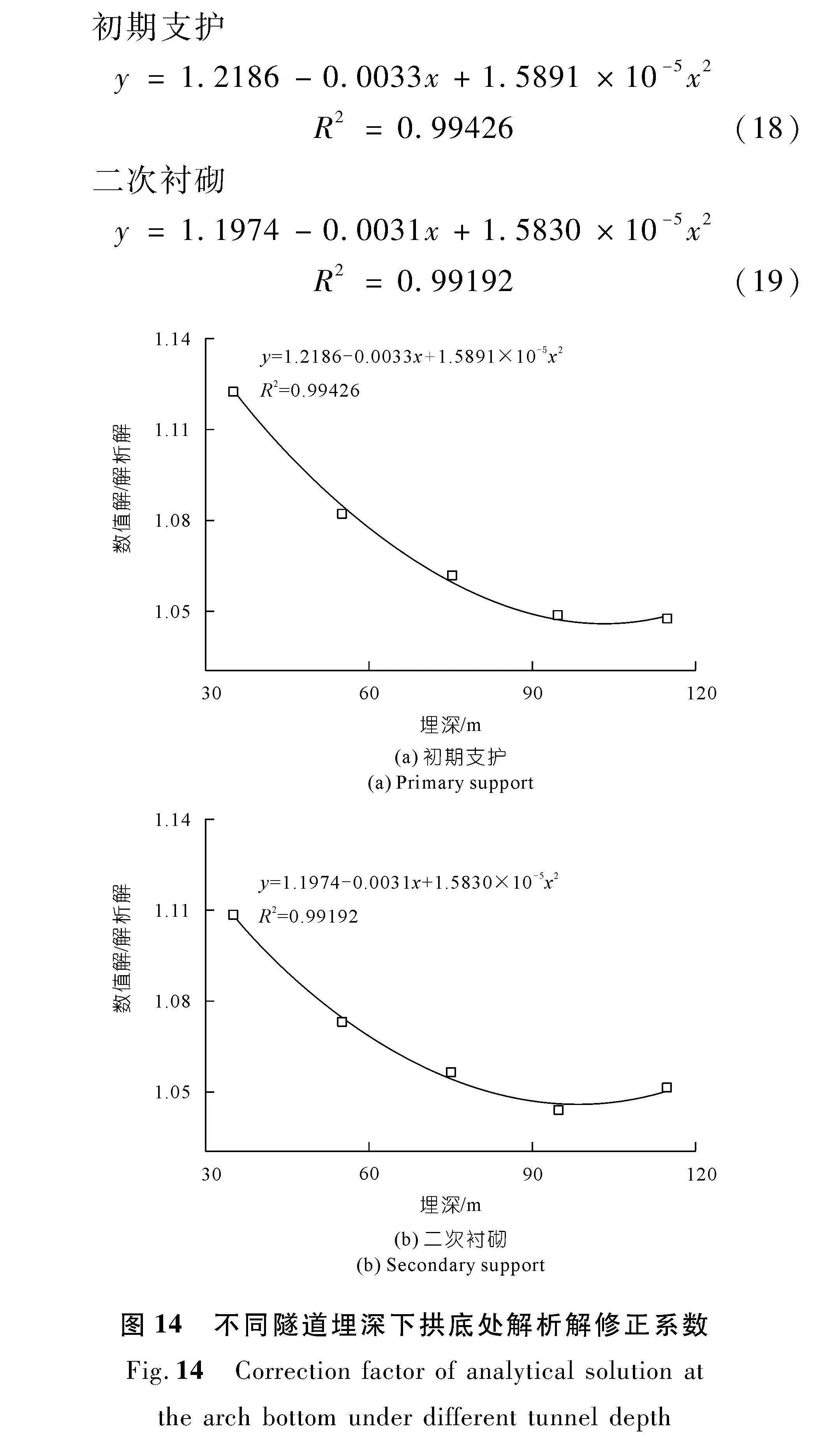
通过第2.3节分析可知，不同埋深下拱底处外水压力解析解计算误差最大值接近13%，为明晰解析解误差变化趋势，绘制拱底处数值解与解析解之比在不同埋深下的拟合曲线，如图14所示。由图14可知，拱底处解析解计算结果偏小，比值随着埋深增大而减小，减小幅度逐渐降低，埋深较小时，需改进已有的解析解得到适用的半解析公式。定义数值解与解析解之比为修正系数，通过拟合得到拱底处初期支护和二次衬砌外水压力解析解修正系数与埋深的曲线方程如下：

初期支护

y=1.2186-0.0033x+1.5891×10-5x2R2=0.99426（18）

二次衬砌

y=1.1974-0.0031x+1.5830×10-5x2R2=0.99192（19）

4" 结 论

通过等效周长法将四心圆形隧道等效为圆形隧道，采用理论计算和数值模拟的研究方法，在不同实际工况下对水下双孔平行隧道镜像法解析解开展了计算误差分析及其影响因素研究，最后依据数值解对解析解进行了修正，得到适用于实际隧道工程渗流场计算的半解析解，主要结论如下：

（1） 对比分析了水下双孔四心圆隧道支护结构外水压力解析解和数值解，发现不同工况下拱顶处基于等效周长理论的解析解计算值偏大，而拱底处解析解计算值偏小。双孔隧道间距和注浆圈厚度对拱顶和拱底处的外水压力分布影响较小，外水压力随埋深呈线性增加趋势，随二次衬砌厚度和注浆圈渗透系数呈指数增加趋势，随二次衬砌渗透系数呈指数降低趋势。初期支护外水压力的折减幅度对二次衬砌结构参数变化的敏感度较大，对埋深、间距和注浆圈参数变化的敏感度较小。

（2） 间距和注浆圈厚度对外水压力解析解计算误差影响较小，解析解计算误差与埋深呈反比关系。拱顶处解析解计算误差随注浆圈渗透系数增加呈指数降低趋势，注浆圈渗透系数对拱底处解析解计算误差影响较小。拱顶处解析解计算误差与二次衬砌渗透性呈正比关系，与二次衬砌厚度呈反比关系。拱底处解析解计算误差与二次衬砌渗透性呈反比关系，与二次衬砌厚度呈正比关系。

（3） 对解析解与数值解计算误差的影响因素进行了灰色关联度分析，发现支护结构渗透系数对拱顶处解析解计算误差影响较大，间距和支护结构厚度对拱底处初期支护外水压力解析解计算误差影响较大，支护结构厚度对拱底处二次衬砌外水压力解析解计算误差影响较大。

（4） 通过数据拟合对双孔四心圆隧道解析解计算误差进行修正，得到了可直接应用于工程的半解析解。拱顶处解析解的修正因素主要为注浆圈渗透系数，注浆圈渗透系数较小时解析解计算误差变化显著。拱底处解析解的修正因素主要为隧道埋深，隧道埋深较小时解析解计算误差变化显著。

参考文献：

［1］" 崔金良，张俊文，万雷，等.基于全景影像的引水隧洞结构缝检测方法及应用［J］.人民长江，2022，53（7）：135-141.

［2］" ZHU Y M，YANG H P，HUANG M Q，et al.External hydraulic pressure and invert uplift study in a non-circular shallow tunnel［J］.Tunnelling and Underground Space Technology，2022，122：104345.

［3］" DUAN S Q，JIANG X Q，JIANG Q，et al.Theoretical solution and failure analysis of water pressure on lining of deep-buried non-circular hydraulic tunnel based on the equivalent hydraulic radius method［J］.Engineering Failure Analysis，2023，148：107163.

［4］" GOODMAN R E，MOYE D G，SCHALKWYK A V，et al.Ground water inflow during tunnel driving［J］.Engineering Geology，1965，2（1）：39-56.

［5］" EL TANI M.Circular tunnel in a semi-infinite aquifer［J］.Tunneling and Underground Space Technology，2003，18（1）：49-55.

［6］" 张丙强.半无限平面双孔平行隧道渗流场解析研究［J］.铁道学报，2017，39（1）：125-131.

［7］" 王帅，王渭明，王晓杰，等.平行三孔海底隧道渗流场解析解及影响参数［J］.中国科技论文，2018，13（13）：1481-1487.

［8］" 应宏伟，朱成伟，龚晓南.考虑注浆圈作用水下隧道渗流场解析解［J］.浙江大学学报（工学版），2016，50（6）：1018-1023.

［9］" 乔彤，周建，张天骄，等.考虑渗透各向异性的水下非圆形隧道渗流场解析［J］.工程科学与技术，2023，55（5）：109-117.

［10］WANG S，LU A，TAO J，et al.Analytical solution for an arbitrary-shaped tunnel with full-slip contact lining in anisotropic rock mass［J］.International Journal of Rock Mechanics and Mining Sciences，2020，128：104276.

［11］朱成伟，应宏伟，龚晓南，等.水下双线平行隧道渗流场解析研究［J］.岩土工程学报，2019，41（2）：355-360.

［12］麻凤海，高冠一.隧道过海段水压力及渗流量计算方法［J］.科学技术与工程，2019，19（18）：290-295.

［13］罗其奇，李萍，周斌，等.基于等效面积法的隧道渗流场解析解应用［J］.科学技术与工程，2017，17（32）：174-180.

［14］王志杰，何晟亚，袁晔，等.基于等效周长法研究隧道衬砌水压力荷载及内力［J］.铁道科学与工程学报，2015，12（3）：577-583.

［15］吴波，路明，雷领等.基于正交试验、组合赋权-灰色关联度法研究隧道施工最优方案［J］.中国安全生产科学技术，2019，15（8）：124-130.

（编辑：郑 毅）

Semi-analytical study on seepage field of underwater twin tunnels based on equivalent theory

PAN Yiheng1，LUO Qiqi2，RUAN Caitian3，CHEN Chao1

（1.College of Harbour and Coastal Engineering，Jimei University，Xiamen 361000，China；" 2.School of Civil Engineering，Central South University，Changsha 410075，China；" 3.Xiamen Branch，China National Aviation Fuel Supply Co.，Ltd.，Xiamen 361006，China）

Abstract：

To study the influence of tunnel design parameters on seepage field of underwater twin tunnels，a seepage calculation model of underwater twin tunnels with two-hole was established.Abaqus was used to build a numerical model.The tunnel burial depth，double hole spacing and support structure parameters were chosen as influencing factors，and the influence of each factor on calculation error of analytical solution based on equivalent method and the variation characteristics of external water pressure acted on the composite lining structure were analyzed.The sensitivity of each influencing factor was studied by grey correlation analysis.Finally，based on the numerical results，the analytical solution was modified and a semi analytical solution with high accuracy was obtained.The result shows that the structural parameters of secondary lining have a significant impact on the reduction of the external water pressure acted on the primary support，while the burial depth，tunnel spacing，and grouting parameters have relatively small impacts on the reduction of the external water pressure on primary support.The permeability coefficient of the support structure has a significant impact on the calculation error of the analytical solution at the vault，and the thickness of the support structure has a significant impact on the calculation error at the arch bottom.When the ratio of burial depth to equivalent radius is less than 19，the calculation error of the analytical solution is approximately 12%.When the ratio of the permeability coefficient of grouting ring to the permeability coefficient of secondary lining is less than 20，the calculation error at the arched bottom exceeds 10%.The permeability coefficient of grouting layer has a large influence on error of analytical solution at vault，while the burial depth has a large influence on error of analytical solution at arch bottom.

Key words：

underwater twin tunnels； seepage； semi-analytical solution； grey relational analysis； external water pressure