水平定向钻穿越水敏性地层冒浆预测及防控

摘要：

非开挖水平定向钻穿越施工中，孔内压力过高会造成地表隆起冒浆事故，严重污染周围环境，造成重大经济损失。以福州市塘坂引水工程供水管道水平定向钻穿越项目为例，考虑工程水敏性软化造浆地层，基于Mohr-Coulomb准则构建了针对水敏弱膨胀地层的孔内最大允许泥浆压力计算模型，并通过现场位移监测数据验证了模型的正确性；随后通过现场应用校验了非开挖水平定向钻穿越水敏弱膨胀地层的冒浆防控技术可靠性。研究结果表明：所推导的计算模型比现有其他孔内允许泥浆压力预测模型更加适用于水敏性软化造浆地层；水平定向钻穿越冒浆防控技术应以孔内泥浆压力控制为主，结合泥浆技术、工艺优化防止憋压，最后辅以局部薄弱点加强、定向控制冒浆等手段进一步加强冒浆预防措施，保障施工安全。

关" 键" 词：

非开挖施工； 水平定向钻； 水敏性地层； 冒浆

中图法分类号： TU992

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.07.022

收稿日期：

2024-01-02

；接受日期：

2024-03-10

基金项目：

国家自然科学基金项目（42002284）

作者简介：

郑" 华，男，高级工程师，主要从事市政给排水管线工程相关工作。E-mail：zhenghua20230810@126.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 07-0167-07

引用本文：

郑华.水平定向钻穿越水敏性地层冒浆预测及防控

［J］.人民长江，2024，55（7）：167-173.

0" 引 言

管道工程是除公路、铁路、水运和航空运输以外的现代生产第五大运输方式，应用范围涵盖市政、水利、交通和油气能源等领域［1］。而水平定向钻工法施工效率高、环境友好、不影响交通，可完全避免传统开挖施工造成的“马路拉链”问题，因而被广泛应用于市政、油气等地下管网建设中［2］。目前针对大直径岩屑颗粒，业界通常采用提高泥浆泵送压力的方法来提高环空泥浆平均流速，以提高孔内岩屑排出效率［3-4］。然而，在非开挖水平定向钻钻进过程中，如果孔内泥浆压力超过周围土体强度极限，钻孔就会发生压裂破坏，从而导致孔内泥浆通过土体裂缝向上涌出至地表（或者涌进江河、湖泊底部），造成地表隆起冒浆事故，严重污染周围环境，造成重大经济损失［5-6］，如图1所示。因此，如何对水平定向钻

穿越地层冒浆情况进行有效防控具有重要研究意义。

目前，国内外学者主要以孔扩张理论为基础开展钻孔周围土体水力压裂破坏机理研究。在非开挖水平定向钻的孔内最大允许泥浆压力计算方面，Hergarden等［7］基于孔扩张理论，推导出孔内Delft公式。后续一些学者对Delft公式进行了改进：如Staheli等［8］对Delft公式中砂层和黏土层的最大塑性区半径进行修正，并得到了国际管道研究会和美国陆军工程兵团的广泛采用；Keulen等［9］分析了土体的破坏情况及判定标准，将Delft公式中的应力改用应变表示，得到基于环向应变的最大允许钻孔液压力公式；Xia等［10］通过理论分析，认为Delft公式预测值偏高，然后假设钻孔周围的塑性区均匀发展，并基于孔扩张理论针对纯黏性土建立了孔壁失稳模型；Lan等［11］考虑孔隙水压力的影响，建立了非开挖水平定向钻孔周围土体破坏机理的判定准则，但并未进行验证。大量国内学者也从地质方面和工程方面［12-13］分析了影响钻孔稳定性的主要因素及钻孔失稳机理，认为影响水平定向钻孔壁稳定的主要因素是钻孔液压力，并得出最优钻孔液压力计算公式。

目前国内学者关于孔扩张理论的研究主要集中在桩基工程中：如龚晓南等［14］假设材料为各向同性的理想弹塑性，分析了抗拉、抗压模量不同的材料圆孔扩张时的应力、位移以及塑性区的发展规律；章定文等［15］基于圆柱孔扩张理论，建立了压力控制边界条件的柱孔扩张数值模型；饶平平等［16］基于统一强度理论，推导了柱孔扩张问题弹塑性解析解。也有国内学者基于孔扩张理论研究，对非开挖水平定向钻进钻孔稳定性进行了一定研究：如孙瑞锋［17］和刘大金［18］根据土力学和弹塑性力学，分析了孔壁周围土体的应力和位移的分布情况；孙平贺等［19］采用快速拉格朗日的计算方法，利用Mohr-Coulomb准则分析了水平定向钻施工过程中泥浆压力对钻孔周围土体位移场和应力场的影响；王建强等［20］在Biot固结理论的基础之上，建立了应力场和渗流场耦合数学模型；曾聪等［21］考虑泥浆渗透侵入对钻孔周围土体应力场分布的影响，通过理论分析和实验室测试的方法推导出水平定向钻钻孔塑性半径公式；刘远亮［22］分析得到了不同钻遇地层的冒浆破坏机理，建立了钻杆内和钻孔环空钻井液压力计算模型以及地层冒浆临界压力计算模型。

但综合来看，上述研究成果较为基础，针对性不强，对夹杂大粒径钙质结核的水敏微膨胀黏土地层的指导意义有限。基于此，本文以福州市塘板引水工程供水管道水平定向钻穿越项目为例，通过理论模型对比分析、数值模拟计算分析、项目现场数据实测相结合的手段，对水平定向钻穿越水敏性特殊地层的冒浆机理及防控措施开展研究。

1" 孔内最大允许泥浆压力理论模型对比分析

表1总结了目前用于预测孔内最大泥浆压力的常见模型，主要有Delft公式、Delft修正公式、Xia公式、Lan公式。

Delft公式认为最大允许塑性半径等于钻孔埋深，虽然Hergarden等根据土体类型对最大塑性半径的取值进行了划分［7］，即在黏性土与无黏性土中，最大塑性半径取值分别为钻孔埋深的1/2与1/3，但大量的工程案例表明，利用Delft公式计算的最大允许泥浆压力值仍偏大，实际工程中在尚未达到该值时便有可能发生孔壁失稳冒浆，因此Delft公式偏于不安全、不保

公式名称公式形式说明

Delft公式Plim=Pf+ccotφR0Rp，max2+Q-sinφ1+sinφ-ccotφ

当塑性区半径无限增大时：

Plim=Pf+ccotφQ-sinφ1+sinφ-ccotφPf=σ′01+sinφ+ccosφ，Q=σ′0sinφ+ccosφG，

Plim为孔内极限泥浆压力；σ′0为初始有效应力；φ为内摩擦角；c为黏聚力；G为不排水剪切模量；R0为钻孔初始半径；Rp，max为最大允许塑性半径

Delft修正公式pmax=［（εt，max2Gσ′0+ccotφ·1+m1-m）1-mn+1·21+m·（σ′0+cot φ）］+cot φεt，max为最大允许塑性应变；m=1+sinφ1-sinφ，n=1+sinΨ1-sinΨ，Ψ为剪胀角

Xia公式当静侧土压力系数K0≤1时：

Pi=Cu+123K0-1P0-

CulnR0Rp，max2+Cu+32K0-1P0G

当静侧土压力系数K0gt;1时：

Pi=Cu+123-K0P0-

CulnR0Rp，max2+Cu+321-K0P0G

Pi为孔内泥浆的临界压力；Cu为不排水抗剪强度；K0为静侧压力系数；P0为初始超载土压力

Lan公式Pmaxσ′υ=0.304HD10.516φ-9.887+0.078 lnK′0+0.4lnφ-0.483+0.708H为钻孔埋深；D为钻孔直径；φ为摩擦角；K′0为有效静侧压力系数；σ′υ为竖向有效应力

守。Delft修正公式将最大允许塑性应变而非塑性半径作为新的孔内最大允许泥浆压力预测模型的判定标准，但在实际钻进过程中最大塑性应变值难以确定，经验取值0.05缺乏依据。Xia公式未考虑临近地表土体的强度，导致计算结果存在一定误差。Lan公式在浅埋（H/D≤50）水平定向钻穿越工程中应用时，会存在较大误差，同时忽略了泥浆滤失形成泥饼对于孔壁稳定性的影响。

2" 水敏弱膨胀地层的孔内最大允许泥浆压力计算模型

依托工程所穿越黏土地层富含亲水性黏土矿物成分，易受泥浆中水分的侵入渗透影响，造成土体软化，物理力学性能降低。因此，需要针对水敏弱膨胀地层修正孔内最大允许泥浆压力计算公式。忽略弱膨胀土其本身的体积膨胀对孔径缩小的影响，将孔内泥浆压力对周围土体的作用简化为柱状小孔扩张的平面应变问题，且假定钻孔周围土体为均匀各向同性的弹塑性半无限空间体，基于Mohr-Coulomb准则，膨胀软化前的土体强度服从公式（1）：

f（σij）=（σr+σθ）sinφ1+2C1cosφ1-（σr-σθ）=0（1）

式中：σr、σθ为钻孔周围土体的法向应力与切向应力；φ1为土体初始内摩擦角；C1为土体初始黏聚力。

遇水软化后，土体强度服从公式（2）：

F（σij）=（σr+σθ）sin φ2+2C2cos φ2-（σr-σθ）=0（2）

式中：φ2为土体遇水膨胀开始软化后的内摩擦角；C2为土体遇水膨胀开始软化后的黏聚力。

假定土体抗压强度之间的关系为σt=kσc，且0lt;klt;1，土体的内摩擦角不变，即φ2=φ1，考虑黏聚力与软化半径大小有关，取：

C2=（1-βre-rre-ri）C1（3）

式中：β为土体膨胀软化参数；re为塑性半径；ri为土体由弹性状态变为塑性状态时的钻孔半径。

在弹塑性交界处，黏聚力满足连续性条件，即re=r，C=C0。联立式（1）～（3）可得：

F（σij）=（σr+σθ）sinφ2+2（1-βre-rre-ri）C1cosφ2-

（σr-σθ）=0（4）

对于弹性材料，平面应变问题的柱形小孔扩张中土体的平衡方程为

dσrdr+σr-σθr=0（5）

将式（4）代入式（5），可得柱形小孔扩张时软化区域（塑性区域）内的应力应变分量为

σθ=2C2cos φ2［ri+re（β-1）-βr］-σr（re-ri）（sinφ2-1）（re-ri）（1+sinφ2）（6）

σr=mr-2sinφ21+sin φ2+C2cotφ2{ri+re（β-1）+sin φ2［3ri+3re（β-1）-2rβ］}（re-ri）（1+3sin φ2）（7）

式中：m为待定系数。

钻孔在泥浆压力的作用下不断向外扩展，钻孔半径扩张到一定程度达到极限时，r=ri，σr=pi，式（7）可化为

pi=mri-2sinφ21+sinφ2+C2cotφ2{ri+re（β-1）+sinφ2［3ri+3re（β-1）-2riβ］}（re-ri）（1+3sin φ2）（8）

由于σr=pi，可求得m：

m=-r2sin φ21+sin φ2i{C2cos φ2［3ri+3re（β-1）-2rβ］+Ccot φ2［ri+re（β-1）］-Pi（re-ri）（1+3sinφ2）}（re-ri）（1+3sinφ2）（9）

在弹塑性交界处，r=re，σr=σe，弹塑性交界处的压力为

σe=mr-2sinφ21+sinφ2e+C2cotφ2{ri+re（-1+β）+sinφ2［3ri+3re（-1+β）-2reβ］}2（re-ri）（1+3sinφ2）（10）

故可得到最大允许泥浆压力计算公式：

Pi=C2cos φ2Mc+Ccot φ2Me-Ccot φ2MaMb（Me+Mcsin φ2）Md+σeMaMb（11）

式中：Ma=re2sinφ21+sin φ2，

Mb=ri-2sin φ21+sinφ2，

Mc=3ri+re（β-3），

Md=（re-ri）（1+3sin φ2），

Me=ri+re（β-1）。

该公式适用于5≤H/D≤50的水敏弱膨胀地层中水平定向钻穿越工程。一般根据勘察报告或室内土工试验，可得到黏聚力、内摩擦角、土体重度、泊松比、弹性模量、软化系数，再结合钻孔设计方案（包括埋深、半径），即可求得水敏弱膨胀地层的孔内最大允许泥浆压力。

3" 数值模拟验证和现场监测

3.1" 有限元模型构建

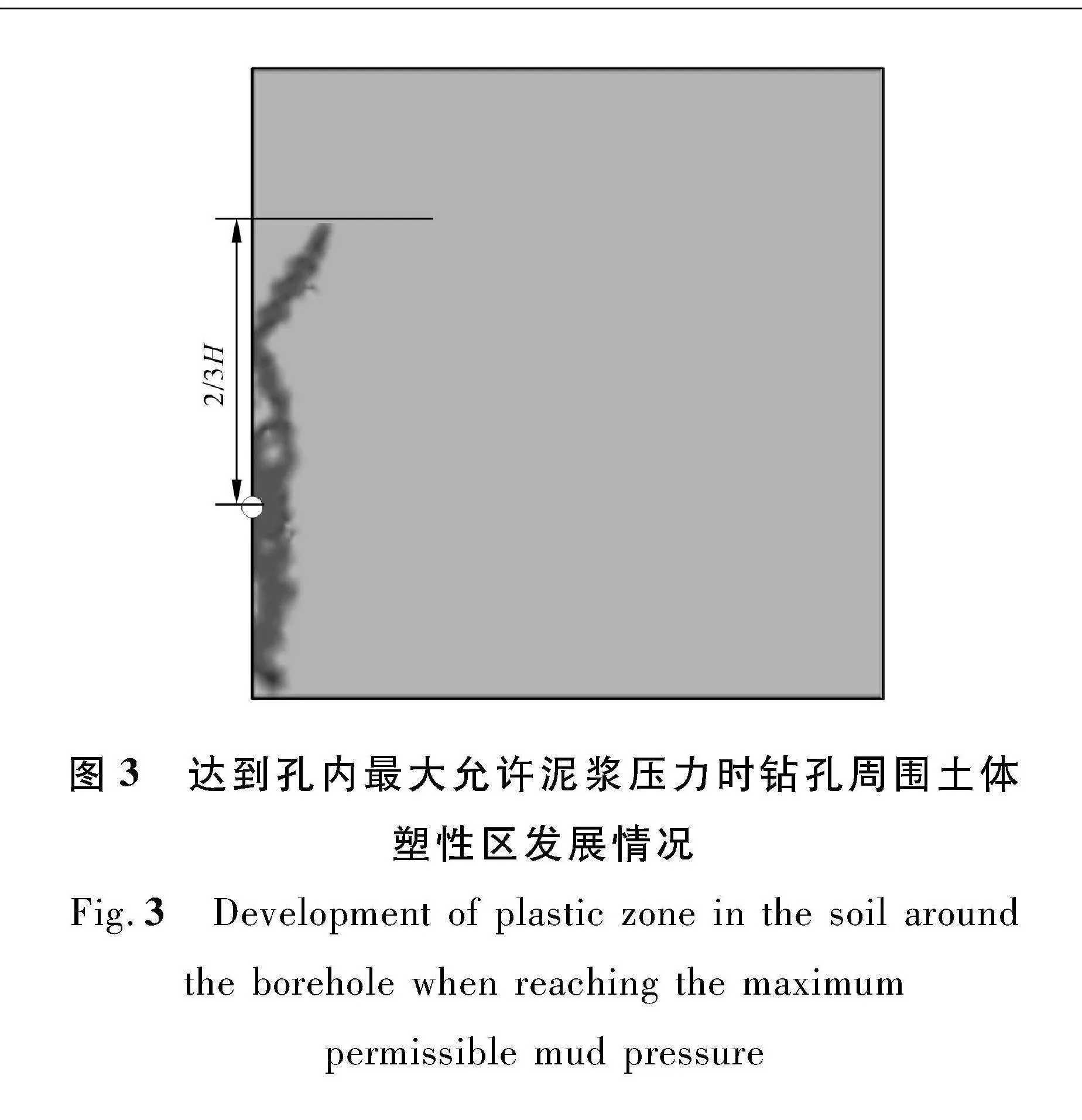
借助采用ABAQUS软件，根据依托工程实际工况，建立二维对称平面模型，模拟孔径为24.13 cm；土体分别为重粉质壤土层、粉质黏土层（图2），设置钻孔距离模型边界为50倍孔径，消除模型边界效应的影响。各层土体的物理力学性质见表2～3。分别约束模型左侧边界的水平位移、底部和右侧边界的水平和垂直位移。模型采用Mohr-Coulomb本构模型，网格采用6节点三角形单元，钻孔周围网格单元加密。钻孔开挖前，首先进行初始地应力平衡，令模型中产生垂直和水平有效应力，然后开挖钻孔区域的单元，并在钻孔孔壁施加径向泥浆压力。该模型将最大塑性区半径扩展至钻孔埋深2/3时的压力作为施工时的孔内最大允许泥浆压力进行提取分析（图3）。

3.2" 现场监测

（1） 泥浆压力监测。

水平定向钻穿越现场为调水工程干渠，为严防渠底冒浆造成水源污染事故，监管部门要求施工过程中孔内泥浆压力须控制在0.38～0.52 MPa之间。在钻进过程中，泥浆压力传感器数据实时传输至地表采集设备，方便对孔内泥浆压力进行不间断监测。

（2） 地表位移变形监测。

地表位移变形是上覆土体对孔内泥浆压力变化响应的表征指标：孔内泥浆压力过高可能造成地表土体隆起，孔内泥浆压力过低可能引起钻孔坍塌进而诱发地表沉降。考虑到此次穿越调水干渠的重要性，针对干渠两岸制定了地表位移监测方案（图4）：在干渠两岸距钻孔设计轴线50 m外的永久占地线附近原状土位置各布置一个基准点，同时位移监测点采用钢钉，布置于干渠两侧马道中间，干渠两岸呈对称式分别布置14个监测点，监测点间距为5 m。

3.3" 结果分析

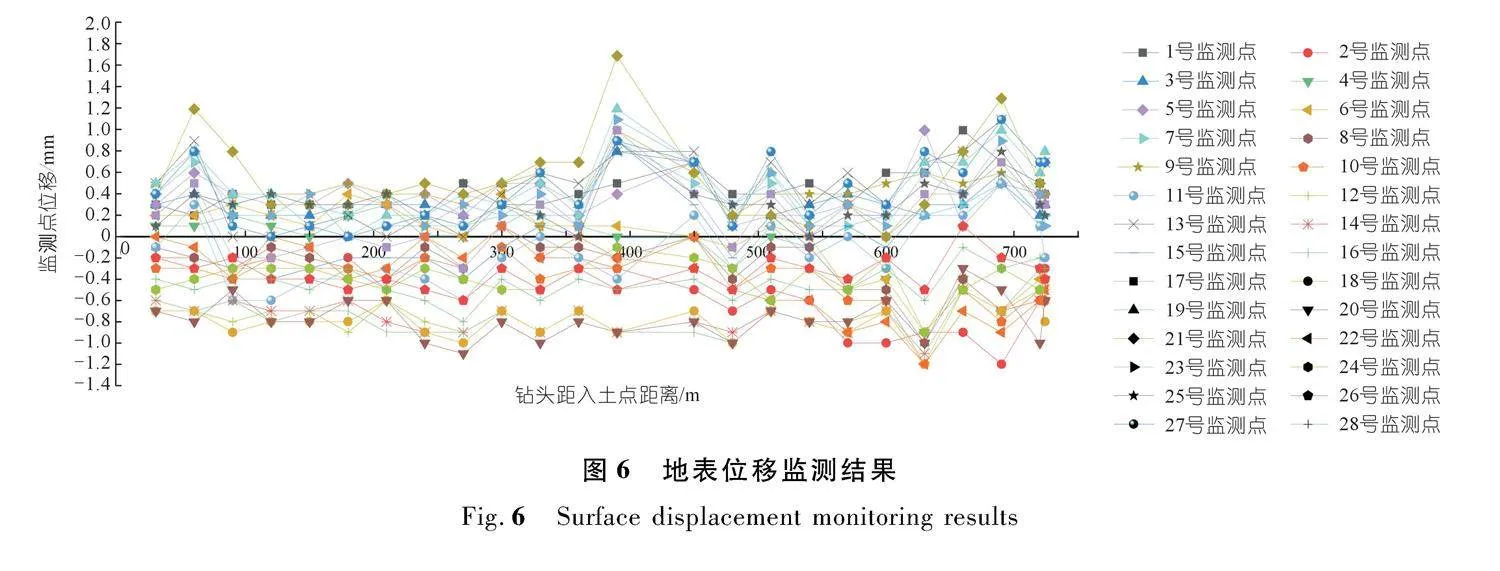
图5展示了现有孔内允许泥浆压力预测模型计算结果、数值模拟结果和现场施工泥浆监测值。通过分析发现，由于干渠正下方土层与钻孔轨迹其他部位相比厚度较薄，所以理论计算模型与数值模拟结果曲线整体均出现“M”形特征，即穿越干渠孔段，孔内泥浆压力需要控制在较低水平。从计算结果整体来看，Delft计算公式结果＞Xia计算公式结果＞Lan计算公式结果＞Delft修正计算公式结果＞数值模拟结果＞本文计算公式结果，其中Delft修正计算公式、数值模拟结果和本文计算公式结果较为接近，这可能是由于数值模拟和本文模型考虑了水敏性地层遇水软化的影响。数值模拟结果和本文计算公式结果大部分处于0.52 MPa以下，仅在干渠两侧马道附近略高于0.52 MPa，这可能是由于设计时未考虑该区域在建设过程中存在的压实过程，而数值模拟和本文计算公式未能充分考虑干渠的钢筋混凝土结构带来的整体抗压能力增强的影响。图6展示了施工期地表位移的监测结果（沉降为正，隆起为负），可知当日地表最大沉降变形发生于21号监测点，最大沉降值为1.7 mm；当日地表最大隆起变形发生于2号、22号监测点，最大隆起值为1.2 mm。各监测点累计沉降或隆起变形未超过20 mm，因此，施工过程中孔内泥浆压力控制在监管压力0.38 MPa以下，有效避免了土体过量变形。数值模拟结果与本文理论计算模型结果拟合程度较好，也较为符合监管压力要求，实际施工过程中未见明显地表变形，证明了理论模型的可行性和合理性。综上，本文建立的水敏弱膨胀地层的孔内最大允许泥浆压力理论计算模型和数值模拟模型是适用的。

4" 水敏弱膨胀地层冒浆防控技术

本文所依托工程的水平定向钻穿越冒浆防控以压力控制为主、局部增强为辅，并针对特殊地层设计适应性泥浆配方、优化钻进工艺，最终实现安全钻进。

4.1" 水敏性地层适应性泥浆配方技术

钻井液在钻进过程中，发挥着动力传递、携带运移岩屑、冷却钻头钻具、维持孔壁稳定以及润滑等作用。

本文所依托工程穿越的地层主要为硬塑-坚硬状粉质黏土，具有水敏性弱膨胀潜势，造浆率较高，同时含较多钙质结核，局部较富集，粒径不均，一般为1～3 cm，个别为6～8 cm，最大可达10 cm，含量10%～20%（图7）。因此，现场所需泥浆应具备良好的岩屑携带能力及较低的滤失量。根据现场工程地质条件，通过大量泥浆试配实验，最终确定初始泥浆配方为：膨润土1%～2%+纯碱0.1%+羧甲基纤维素（CMC）0.1%+聚丙烯酰胺（PAM）0.1%。通过现场观测，泥浆流动性较好，黏度合适，携带钻屑能力强（图8）。

4.2" 浅表地层套管隔离技术

工程现场采用规格为φ406 mm的无缝钢管（图9，长60 m）对浅表层杂填土和粉质黏土进行隔离，一方面有效增大返浆通道，确保返浆通畅；另一方面也避免了钻屑在孔口淤积，造成孔口堵塞。

4.3" 优化钻进工艺

考虑到地层特殊性，在钻进工艺方面作如下优化：① 在穿越黏土层时，采用较低钻速，且每进尺一根钻杆，洗孔一次，这样不仅可以反复机械碾压充分破碎钙质结核，同时也降低了卡钻的风险，保证钻孔通畅；② 严格控制泥浆泵量，在前半段导向孔钻进时选用较大泵量，可快速携带出钻屑，防止孔内淤堵，在后半段导

向孔钻进时选用较小泵量，并时刻注意返浆情况，避免孔内憋压。

4.4" 泄压孔“造瘘”技术

钻导向孔前，在干渠两侧靠近永久占地围栏处各设置1个泄压孔，孔径为100 mm，深度与所在位置的钻孔轨迹齐平，水平间距不超过5 m。如图10所示，当孔内发生阻塞泥浆压力升高时，泥浆可通过击穿泄压孔排出至地表，将不可预知、不可控的冒浆事故转化为可控的定向冒浆处理。

5" 结 论

本文基于Mohr-Coulomb准则，考虑泥浆渗透侵入造成的土体软化，推导出了针对水敏弱膨胀地层的孔内最大允许泥浆压力计算模型，然后与数值模拟结果和现场监测数据进行对比，以验证理论模型的可靠性、正确性，并对非开挖水平定向钻穿越水敏弱膨胀地层的冒浆防控技术进行现场应用校验，得到的主要结论如下：

（1） 考虑到水敏弱膨胀地层在泥浆中水分作用下会发生软化，造成力学性能降低，基于Mohr-Coulomb准则，建立了针对水敏弱膨胀地层的孔内最大允许泥浆压力计算模型，并可根据勘察报告（包括土体物性参数）、钻孔轨迹设计方案进行了参数求解。

（2） 根据依托工程的已知参数，利用该理论模型求解的孔内泥浆压力控制区间与数值模拟结果基本吻合，结合现场地表位移监测结果，可以证明该理论模型和数值模拟模型的合理性和适用性，更加适用于5≤H/D≤50的水敏弱膨胀地层中水平定向钻穿越工程。

（3） 水平定向钻穿越工程中，采用何种冒浆防控技术应充分考虑项目场地的工程地质条件，因地制宜。首先以孔内最大允许泥浆压力预测结果作为施工控制压力；然后针对特殊敏感地层，还需要特别调制专用泥浆配方（膨润土1%～2%+纯碱0.1%+羧甲基纤维素0.1%+聚丙烯酰胺0.1%）；接着通过优化钻进工艺，降低孔内岩屑堆积，保障泥浆循环通路，避免钻孔憋压；最后针对性地对穿越轨迹上特殊的薄弱点进行局部加强（如套管隔离技术）或定向控制冒浆（如泄压孔“造瘘”技术）。结合上述思路，可针对具体工程定制专属冒浆防控方案，保障施工安全。

参考文献：

［1］" 马保松.非开挖工程学［M］.北京：人民交通出版社，2008.

［2］" MA B，NAJAFI M.Development and applications of trenchless technology in China［J］.Tunnelling and Underground Space Technology，2008，23（4）：476-480.

［3］" SHU B，MA B.The return of drilling fluid in large diameter horizontal directional drilling boreholes［J］.Tunnelling and Underground Space Technology，2016，52：1-11.

［4］" YAN X，MA B，ZENG C，et al.Analysis of formation fracturing for the Maxi-HDD Qin River crossing project in China［J］.Tunnelling and Underground Space Technology，2016，53（3）：1-12.

［5］" FRANCIS M，KWONG J，KAWAMURA K.Analysis of heave and subsidence risk for horizontal directional drilling［C］∥ International Conference on New Pipeline Technologies，Newjersey，2003.

［6］" LUEKE J S，ARIARATNAM S T.Experimental procedure for evaluating ground displacement factors in directional drilling［J］.Canadian Journal of Civil Engineering，2003，30（5）：830-840.

［7］" HERGARDEN H，LUGER H J.Directional drilling in soft soil：influence of mud pressures［C］∥ Proceedings of the International No-Dig Conference，Washington D.C.，1988.

［8］" STAHELI K，BENNETT R D，O’DONNELL H W，et al.Installation of pipelines beneath levees using horizontal directional drilling［M］.Vicksburg：Geotechnical Laboratory （U.S.） Engineer Research and Development Centre，1998.

［9］" KEULEN B，ARENDS G，MASTBERGEN D R.Maximum allowable pressures during directional driing focused on sand［J］.Delft Geotechnics Thesis Paper，2001（23-32）：39-74.

［10］" XIA H，AND MOORE I D.Discussion of limiting mud pressure during directional drilling in clays［J］.Ottawa GEO，2007：1696-1701.

［11］" LAN H，MOORE I D.Practical criteria for borehole instability in saturated clay during horizontal directional drilling［C］∥The North American Society （NASTT） and the Internationa Society for Trechless Technology （ISTT） International No-Dig Show，2016：TM2-T2-01.

［12］" 王建钧.水平定向钻孔应力-应变及失稳机理研究［D］.昆明：昆明理工大学，2008.

［13］" 樊琦.水平定向钻孔孔壁稳定性分析及工程应用研究［D］.西安：西安科技大学，2010.

［14］" 龚晓南，王启铜.拉压模量不同材料的圆孔扩张问题［J］.应用力学学报，1994（4）：127-132.

［15］" 章定文，韩文君，刘松玉.初始应力各向异性状态下圆柱孔扩张机制分析［J］.岩土力学，2010（增2）：104-108.

［16］" 饶平平，李镜培，张常光.考虑各向异性、剪胀和渗流的柱孔扩张问题统一解［J］.岩土力学，2010（增2）：79-85.

［17］" 孙瑞锋.城市地下管道非开挖技术的岩土力学研究［D］.重庆：重庆大学，2005.

［18］" 刘大金.土体中水平钻孔孔壁稳定性分析及试验研究［D］.长春：吉林大学，2006.

［19］" 孙平贺，安传德，曹函.基于钻液压力的非开挖近孔壁位移响应数值分析［J］.地下空间与工程学报，2011，7（6）：1168-1173.

［20］" 王建强，李国民，赵洪波，等.流固耦合作用下水平定向孔壁稳定性分析［J］.地下空间与工程学报，2012，8（4）：796-801.

［21］" 曾聪，马保松，刘厚平.水平定向钻穿越施工中钻井液渗透对孔壁塑性半径的影响［J］.中国石油大学学报（自然科学版），2013，37（2）：57-61.

［22］" 刘远亮.水平定向钻进铺管防冒浆技术研究［D］.武汉：中国地质大学（武汉），2010.

［23］" 吴云刚.南水北调中线工程膨胀土膨胀本构模型试验研究［D］.武汉：中国地质大学（武汉），2011.

（编辑：胡旭东）

Prediction and prevention of mud-bursting during horizontal directional drilling through water-sensitive strata

ZHENG Hua

（Fuzhou Water Engineering Co.，Ltd.，Fuzhou 350025，China）

Abstract：

In the construction of non-excavation horizontal directional drilling，the high pressure in the hole can cause surface uplift and slurry accident，seriously polluting the surrounding environment，and causing major economic losses.Taking the horizontal directional drilling crossing project of water supply pipeline in Tangban Water Diversion Project in Fuzhou City as an example，considering that the project is located in water-sensitive softening slurry formation，a targeted calculation model of maximum allowable mud pressure in the hole was constructed based on Mohr-Coulomb criterion，and the correctness of the model was verified by field displacement monitoring data.Then，the reliability of slurry prevention and control technology for non-excavation horizontal directional drilling through water-sensitive weak expansive strata was verified by field application.The results showed that the constructed calculation model in this paper was more suitable for water-sensitive softening slurry formation than other existing prediction models.The mud-bursting prevention should focus on the control of mud pressure in the hole，while combining with mud preparing technology and process optimization to prevent pressure suppressing，and finally supplemented by local weak points strengthening，directional control on slurry and other means，so as to ensure construction safety.

Key words：

non-excavation construction； horizontal directional drilling； water-sensitive formation； mud-bursting