非对称顶推力作用下盾构隧道结构响应研究

摘要：

为研究盾构在小半径曲线隧道施工时非对称顶推力对隧道结构力学性能的影响，以广东圭峰山隧道区间盾构隧道为工程背景，考虑隧道衬砌材料的非线性特性，基于混凝土损伤塑性本构模型，建立盾构隧道施工阶段精细化有限元模型，采用数值方法分析了非对称顶推力作用下盾构隧道的力学特性。研究结果表明：①" 在非对称推力作用下盾尾衬砌管片横断面变形表现为向大荷载侧的挤出变形，非对称推力的影响范围与推力偏差量相关。② 非对称推力引起的隧道竖向和横向弯矩远大于环向弯矩，其对环向内力影响较小，且主要体现为对环向剪力的影响。③ 盾构推进油缸的推力偏差使得隧道纵向由全断面受压状态逐渐过渡到压弯状态，在大推力侧的盾尾衬砌环缝（尤其是“T”形缝）间产生了明显的压应力集中，若该区域存在拼装误差，极易造成管片混凝土压溃；而小推力侧的纵向螺栓随着各组油缸推力偏差的增大开始受拉，使得部分环缝处于纵向受拉状态，存在潜在的环缝防水失效风险。因此，进行盾构曲线掘进施工时，应合理调配各组油缸推力，严格控制盾构衬砌管片拼装质量，同时应加强盾尾附近衬砌接缝的渗漏水监测。

关" 键" 词：

盾构隧道； 曲线掘进； 非对称推力； 混凝土损伤塑性模型； 数值模拟； 圭峰山隧道

中图法分类号： TU91

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.07.020

收稿日期：

2023-05-26

；接受日期：

2023-08-29

基金项目：

国家自然科学基金青年基金项目（52208381）

作者简介：

余国武，男，高级工程师，硕士，主要从事高速铁路、城际铁路项目建设管理工作。E-mail：zztl@grci.com.cn

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 07-0151-09

引用本文：

余国武，梁广林，祁军，等.

非对称顶推力作用下盾构隧道结构响应研究

［J］.人民长江，2024，55（7）：151-159.

0" 引 言

盾构工法由于具有安全高效、绿色环保等诸多优点，逐渐成为城市水工隧道、地铁等基础设施修建时最受青睐的施工工法［1］。作为盾构隧道最基本的结构单元，衬砌管片的力学性能直接影响着隧道结构的安全性与可靠性。相比于正常使用阶段，施工阶段管片所承受的荷载较为复杂。叶飞等［2］针对施工期盾构隧道管片的受力特性进行了研究，将施工阶段管片衬砌的受力特性归纳为典型三维特性、不确定性及不可忽视性等3个方面。另一方面，现有工程经验及相关调查也表明，相对于正常使用阶段，施工阶段极易造成管片的破损［3-5］。可见，进行施工阶段管片的力学性能分析很有必要。

苏昂等［6］对国内某地铁隧道管片施工病害进行了调查，并对其特征和成因进行了分析，认为导致施工期管片衬砌发生裂损病害的主要原因是盾构施工过程中所产生的不良施工荷载和不良接触状态。而在盾构隧道施工中，千斤顶荷载是衬砌管片在隧道轴向受到的最大外力［7］。在盾构施工过程中，尤其是曲线段掘进时，为满足线路线型要求，需通过调整各分区油缸的推力以实时控制盾构机姿态。不均匀的顶推力会在隧道轴向产生附加弯矩，在该附加弯矩作用下管片局部将会出现应力集中现象，进而产生裂纹，随着千斤顶推力的增大进而出现破损。

目前，国内外学者针对施工阶段管片的受力特性开展了大量研究，但由于施工阶段管片所受荷载及约束条件的复杂性，研究手段仍以有限元法为主［8-12］。然而，现有研究中对钢筋混凝土管片进行了简化，将其视为线弹性材料，忽略了材料本身的属性。混凝土是一种多相复合材料，假定其为弹性体并不能真实反映混凝土应变软化、刚度退化、塑性变形等非线性特性［13］。为此，本文依托圭峰山隧道区间盾构隧道工程，考虑管片材料的非线性特性，基于混凝土损伤塑性本构模型，考虑盾构隧道管片接头的接触关系，采用ABAQUS有限元软件建立了盾构隧道施工期精细化有限元模型，采用有限元方法，对盾构曲线掘进时非对称顶推力作用下的隧道结构响应进行研究。

1" 工程背景

1.1" 工程概况

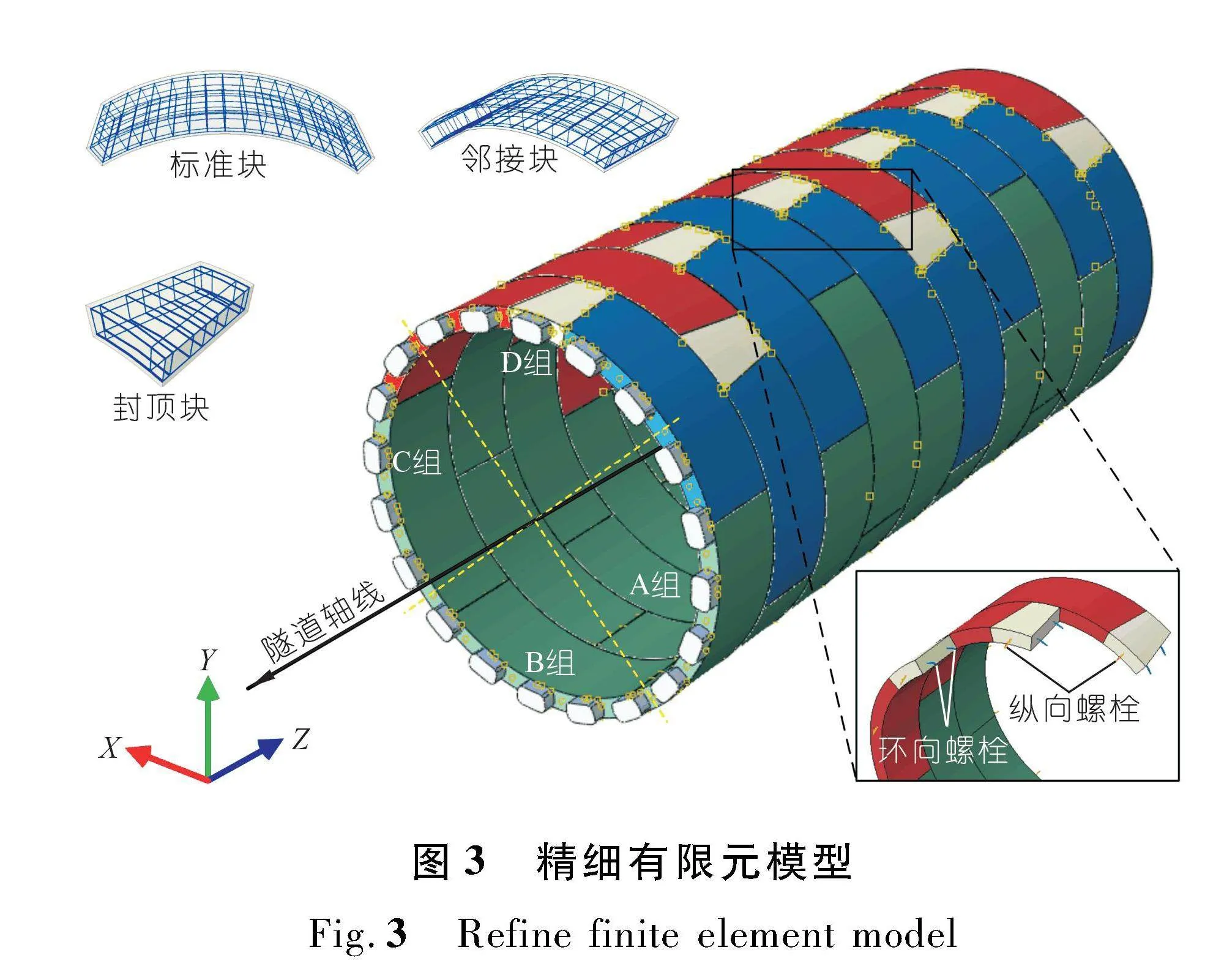
圭峰山区间隧道采用盾构法施工，根据线路设计，隧道左右线盾构均需在圆曲线上始发，其中左线设计始发平曲线半径为400 m，右线设计始发平曲线半径为350 m。隧道左右线间距为12.5～16.5 m，顶部覆土厚度约为8.49～27.18 m。隧道衬砌采用通用楔形管片，管片内径5 400 mm，外径6 000 mm，环宽1 200 mm，楔形量为36 mm。管片衬砌构造如图1所示，每环衬砌由1块封顶块（F块）、2块邻接块（L块）和3块标准块（B块）组成。管片环间错缝拼装，环间采用10只M 24的纵向螺栓连接，每环管片采用12只M 27的环向螺栓连接。衬砌管片混凝土采用C50高强混凝土，钢筋采用HPB300和HRB400级钢筋（主筋采用HRB400E抗震钢筋），螺栓采用机械性能为5.8级的高强螺栓。

1.2" 工程地质条件

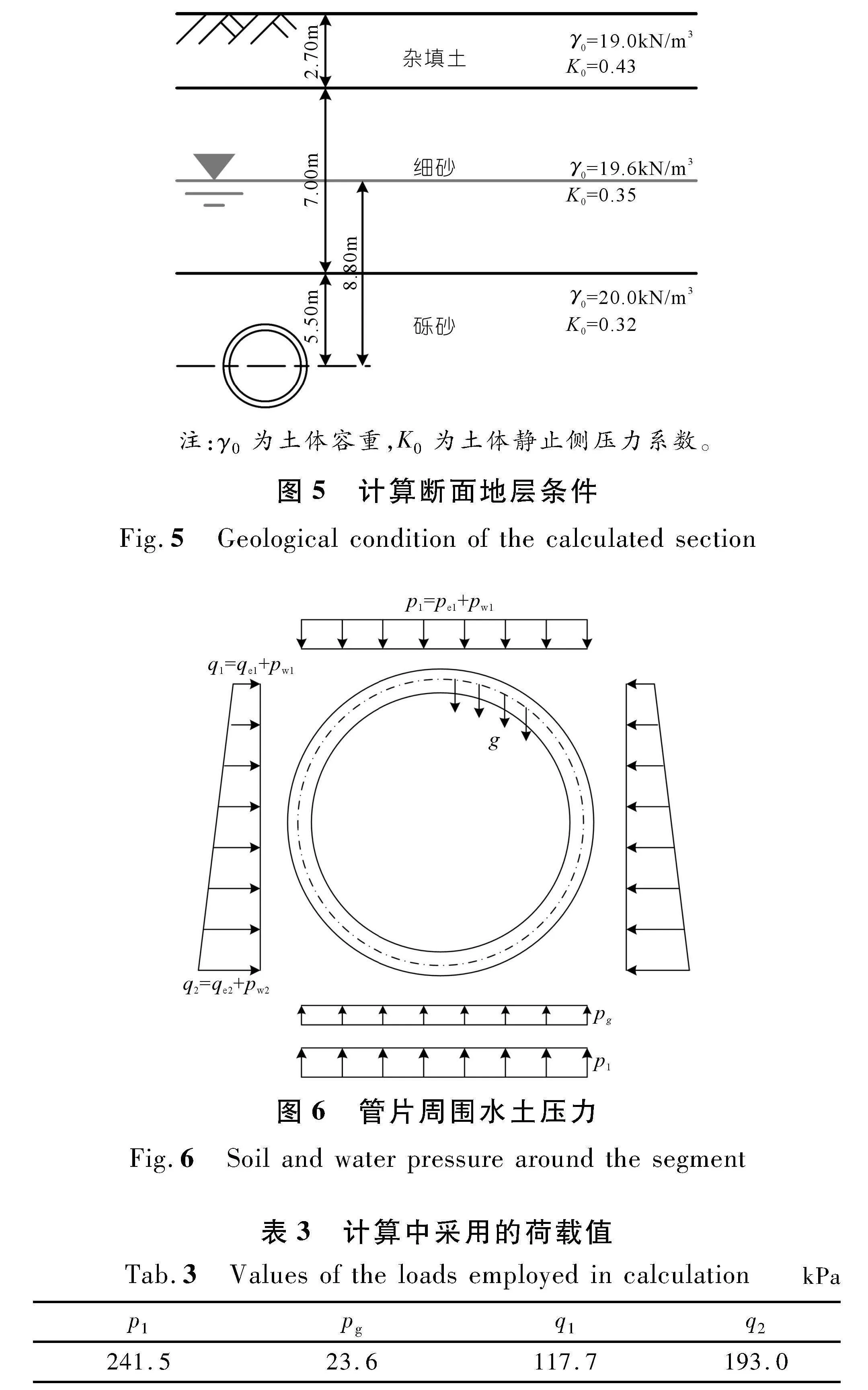
根据勘察资料，场区内地质条件如图2所示（以右线为例），场地地层主要为：杂填土、粉质黏土、细砂、砾砂，下伏第三系新余群基岩。基岩层顶埋深约18.00～21.40 m，强风化泥质粉砂岩平均厚度一般为1.0 m左右，以下为⑤1-3中风化泥质粉砂岩，局部间夹含⑤4钙质泥岩。盾构始发后先全断面穿越砾砂层，通过砂-岩复合地层后过渡至全断面中风化泥质粉砂岩中。

2" 有限元分析模型

2.1" 模型概述

为充分考虑盾构隧道施工阶段的三维特性，正确合理地评价盾构在曲线段掘进时非对称千斤顶推力对隧道结构力学性能的影响，基于区间隧道实际结构参数和掘进参数，采用通用有限元软件ABAQUS建立盾构隧道施工阶段精细化荷载-结构模型，为满足模拟精度，模型沿隧道纵向取10环。建立的管片错缝拼装有限元模型如图3所示。

计算模型由千斤顶撑靴、管片、钢筋及接头螺栓组成，其中管片和千斤顶撑靴采用C3D8R实体单元模拟，钢筋采用T3D2桁架单元模拟，螺栓采用B31梁单元模拟，并将螺栓和钢筋单元嵌入到管片实体单元中。衬砌环内及环间管片之间的切向接触采用Cloumb摩擦接触，摩擦系数取μs = 0.62［14］，法向接触采用硬接触。

模型边界采用位移边界，参考张鹏［9］的建议，约束盾尾第10环衬砌端部的法向位移。

2.2" 材料本构关系

2.2.1" 衬砌管片材料本构模型

为真实反应管片在施工阶段的力学特性，本文采用混凝土损伤塑性模型（CDP）模拟隧道管片的力学行为。由于管片材料的现场试验数据缺失，本文结合混凝土结构设计规范［15］确定管片CDP模型的应力-应变关系。

由于CDP模型采用的是等向强化模型［16～17］，即初始拉压刚度一致，为此本文根据张占廷等［18］建议，取0.4fc，r（fc，r为混凝土抗压强度代表值，本文模型中衬砌管片强度等级为C50，根据规范［15］取fc，r = 32.4 MPa）对应的割线模量为线弹性阶段的初始刚度E0。

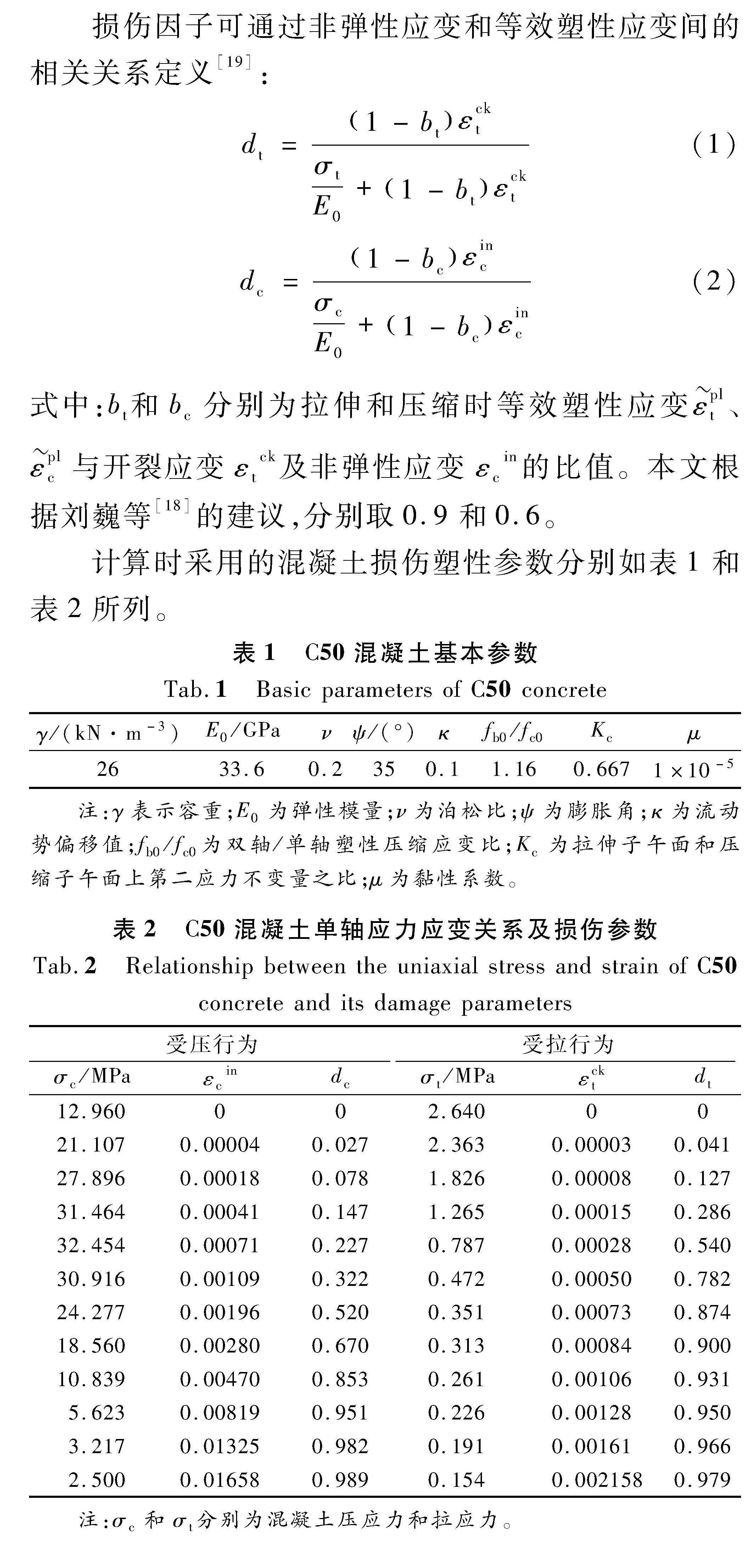
损伤因子可通过非弹性应变和等效塑性应变间的相关关系定义［19］：

dt=1-btεcktσtE0+1-btεckt（1）

dc=1-bcεincσcE0+1-bcεinc（2）

式中：bt和bc分别为拉伸和压缩时等效塑性应变εplt、εplc与开裂应变εtck及非弹性应变εcin的比值。本文根据刘巍等［18］的建议，分别取0.9和0.6。

计算时采用的混凝土损伤塑性参数分别如表1和表2所列。

2.2.2" 螺栓及钢筋本构模型

环、纵向接头是盾构隧道管片衬砌的薄弱环节，因此本文假定螺栓为理想弹塑性材料，其本构关系为

σs=Esεs" εs≤εy

fy，r" εsgt;εy

（3）

式中：σs为螺栓应力；εs为螺栓应变；Es为螺栓的弹性模量；fy，r为螺栓屈服强度代表值；εy为与fy，r对应的螺栓屈服应变。本文中，由于接头螺栓机械性能等级为5.8级，参考文献［20］，取Es = 2.10×105 MPa，fy，r = 400 MPa。

根据模型试算结果，衬砌内钢筋应力一般小于其屈服强度，为此考虑模型的收敛性和计算成本，钢筋采用线弹性本构模拟。根据实际采用的钢筋级别并结合混凝土设计规范［15］确定本文所采用的HPB300和HRB400级钢筋弹性模量分别取2.10×105 MPa和2.00×105 MPa。

2.3" 模型荷载系统

相比于正常使用阶段，盾构隧道管片在施工阶段除承受水土压力外，施工荷载对隧道结构有着显著影响，且在部分管片中施工荷载成为主要荷载。计算模型中管片所受荷载纵向分布如图4所示。

由图4可知，作用在隧道结构上的荷载系统由水土压力、千斤顶推力、注浆压力和地层抗力组成。由于盾壳的保护，盾尾第1环和第2环的一半只作用有千斤顶压力，其外壁不受周围水土压力和注浆压力作用。考虑注浆压力的作用范围，模型中第2环后半环至第5环管片承受注浆压力作用。第6～10环认为注浆浆液已经凝固，管片环承担周围地层的水土压力。

2.3.1" 水土压力

本文水土压力计算断面选取区间隧道曲线段典型断面，计算断面地层条件如图5所示。由于场区地层以砂层为主，因此根据文献［20］建议，进行水土压力计算时水土分算。本文采用的水土压力荷载系统如图6所示，图中p1为隧道顶部的水土压力，g和pg分别为管片自重和由于自重引起的地层反力，q1和q2分别为隧道顶部和底部的侧向水土压力。根据地层条件计算得荷载值如表3所列。

2.3.2" 注浆压力

施工阶段衬砌所受的注浆压力在环向和纵向的分布比较复杂，通常需要引入一些假定来确定盾构隧道壁后注浆压力的变化规律。

由于本文重点研究施工阶段千斤顶推力对隧道结构的影响，因此对注浆压力的分布进行一定的简化。计算模型中采用的注浆压力纵向分布如图4所示，注浆压力自盾尾由0.3 MPa呈线性减小至0。其环向分布采用均匀分布模式。

2.3.3" 地层抗力

在荷载-结构模型中，地层与隧道之间的相互关系通过设置全周仅受压地基弹簧来描述。考虑到盾构推力由管片衬砌和地层的摩阻力抵消，因此，在模型中设置轴向地基弹簧以反映管-土相互作用。

本文中根据隧道所处地层特性并参考文献［21-22］，地基反力系数取10 MPa/m。根据Chaipanna等［12］的建议，轴向地基弹簧刚度取径向地基弹簧刚度的1/3。

此外，为与注浆压力的变化相适应，本文模型中在注浆压力作用段地基弹簧刚度随着注浆压力的减小逐渐增大，如图4所示。

2.3.4" 千斤顶推力

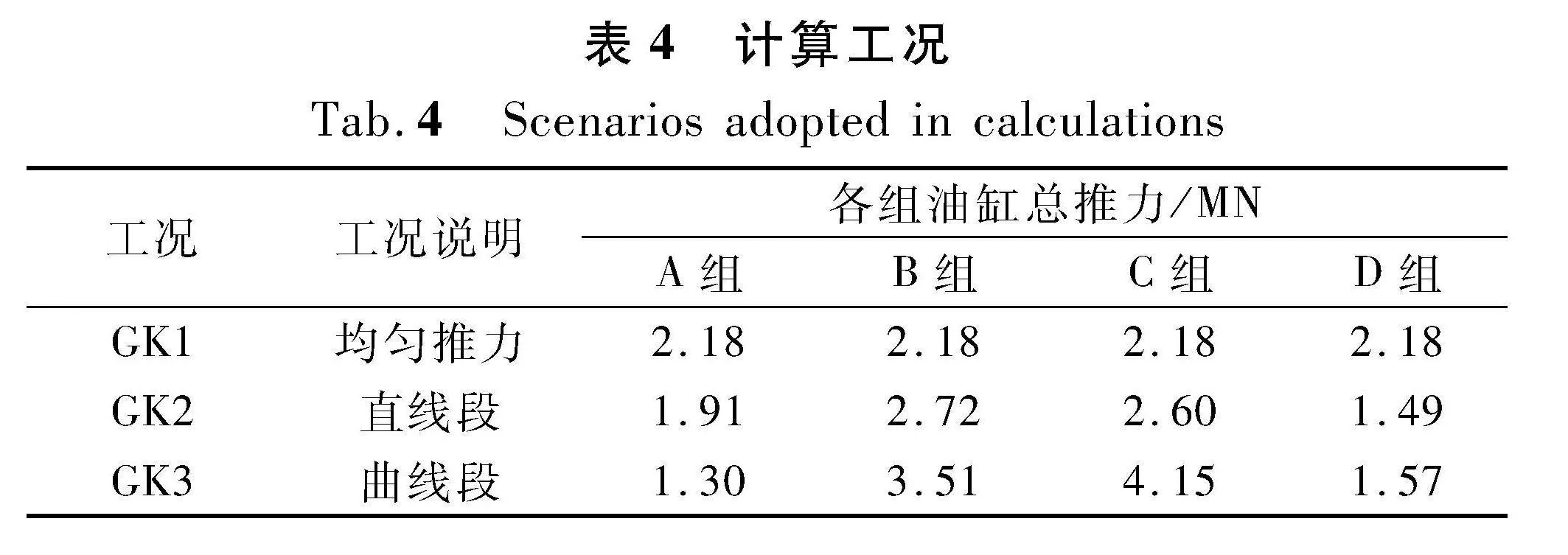
在有限元模型中，按实际盾构推进油缸布置对千斤顶撑靴进行分区，以实现非均匀顶推力的加载。为反映非对称推力的影响，设置一均匀顶推力工况作为对照组。分析工况如表4所列。计算工况中GK2和GK3工况对应的盾构油缸推力为依托工程盾构在曲线段和直线段掘进时的实际推力统计值；GK1中各组油缸推力根据盾构在直线段掘进时的总推力计算得到。

3" 计算结果分析

3.1" 隧道变形

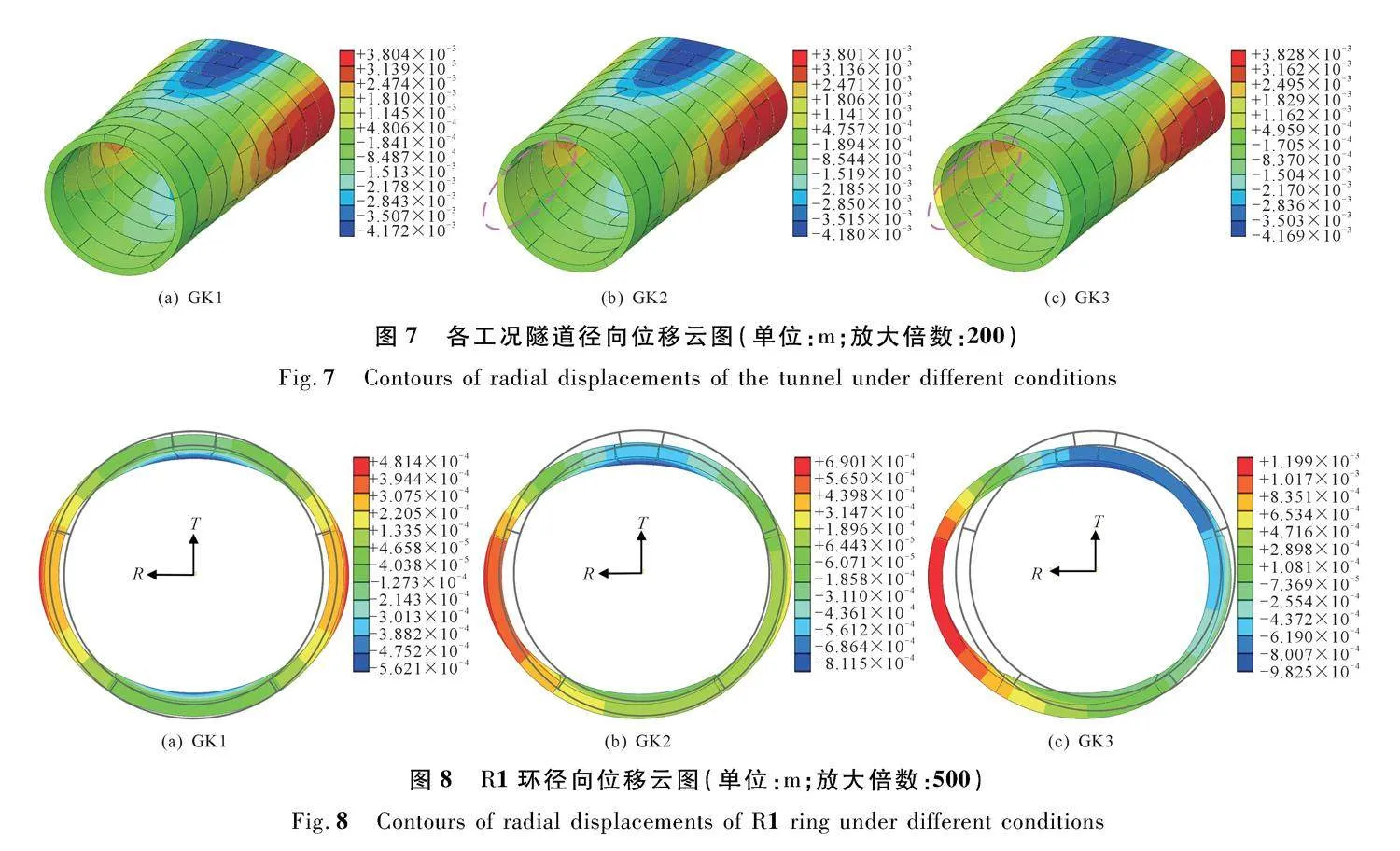
图7为不同计算工况下隧道径向位移云图。由图可见，由于沿隧道纵向荷载分布不同，隧道横断面变形特征沿纵向不尽相同。在水土压力作用段，隧道横断面变形呈典型的“横鸭蛋”形，隧道最大径向位移也发生在该范围内，各工况下管片最大径向位移相近，拱顶处径向位移约为-4.2 mm，拱腰处径向位移约为+3.8 mm。千斤顶推力对隧道横向变形的影响主要集中在盾尾附近的几环衬砌中，相比于均匀的顶推力，推力的非对称性使得盾尾管环横向变形也呈现出非对称性。

图8为盾尾第1环衬砌（R1环）径向位移云图。由图可见，由于R1环衬砌仅在纵向承受千斤顶推力，而在环向不受力，因此其径向位移较小。由于在GK3中各组油缸推力差异最大，因此R1环最大径向位移出现在GK3中，约为1.20 mm，比GK1中均匀推力作用下R1环的最大径向位移（0.48 mm）增大150%。此外，在非对称推力作用下盾尾管环的横断面变形表现为向大荷载侧的挤出变形，其横向变形与纵向推力的分布相关。

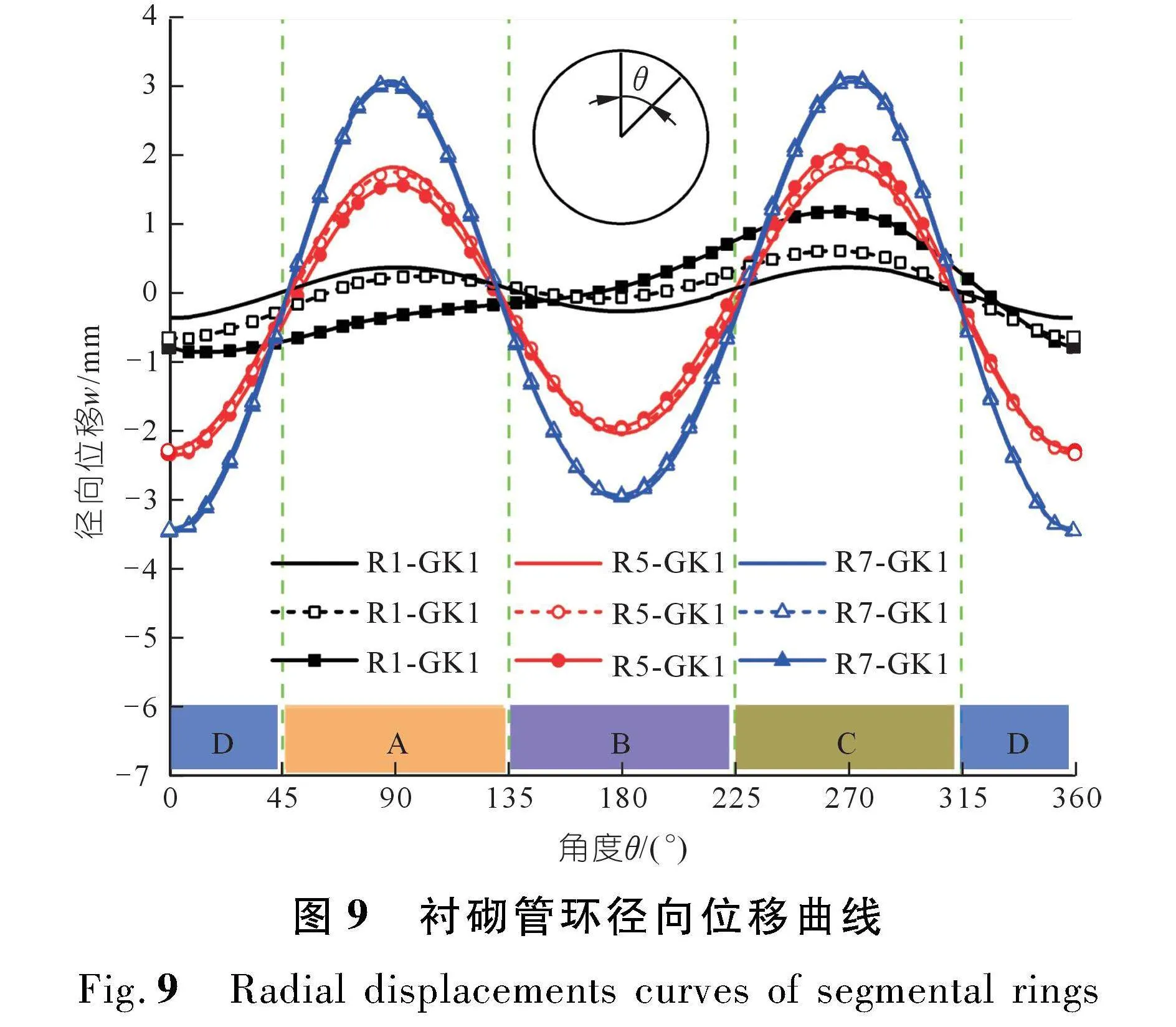
图9为各工况下沿隧道纵向不同位置处各环衬砌

径向位移变化曲线。由图可见，随着距盾尾距离的不断增加，偏心推力的影响不断减弱。在本文设定的计算工况中，GK1中偏心推力的纵向影响范围约为盾尾后5环管片衬砌，而GK2中偏心推力的影响范围约为盾尾后7环管片衬砌。

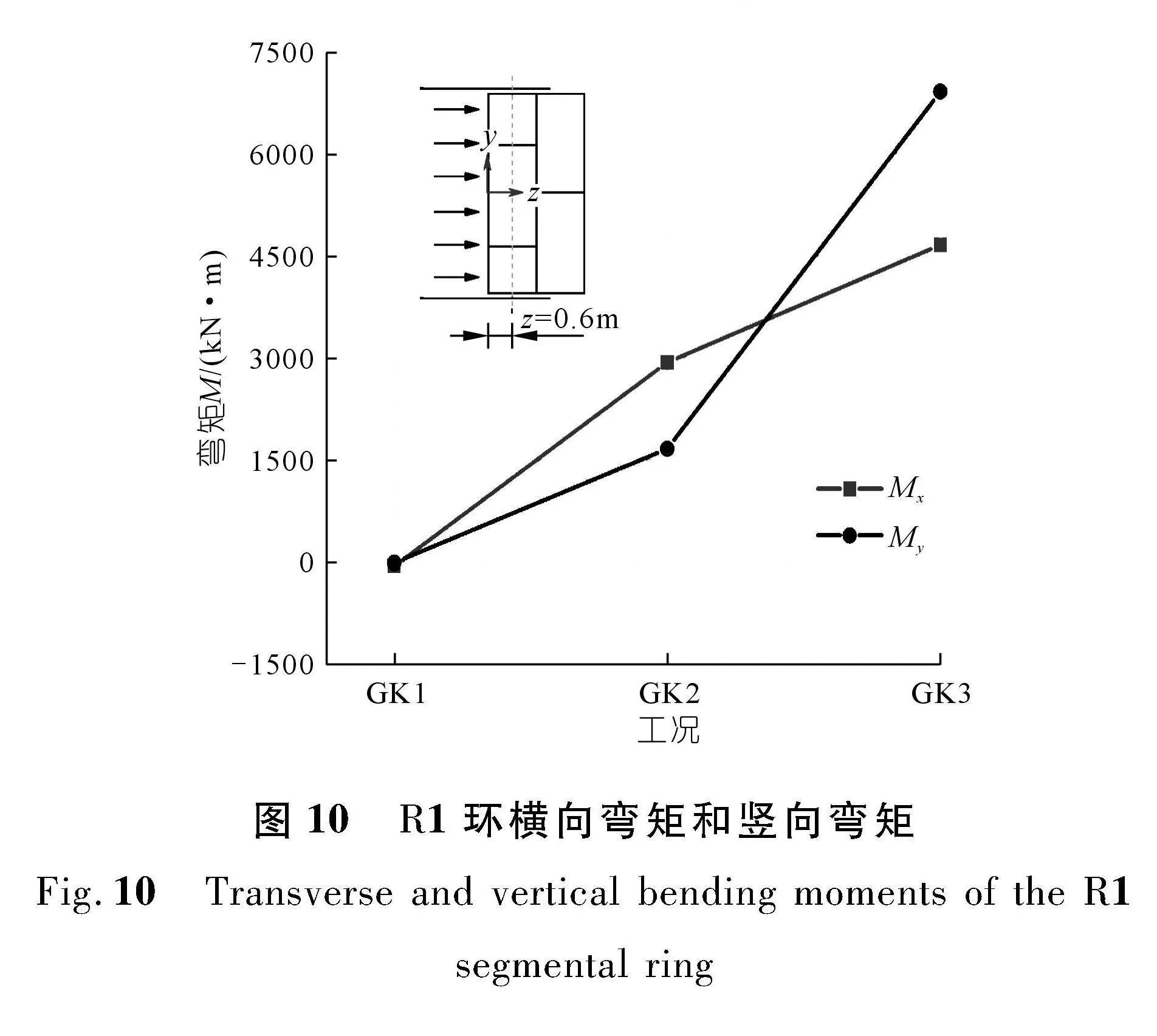
3.2" 管片内力

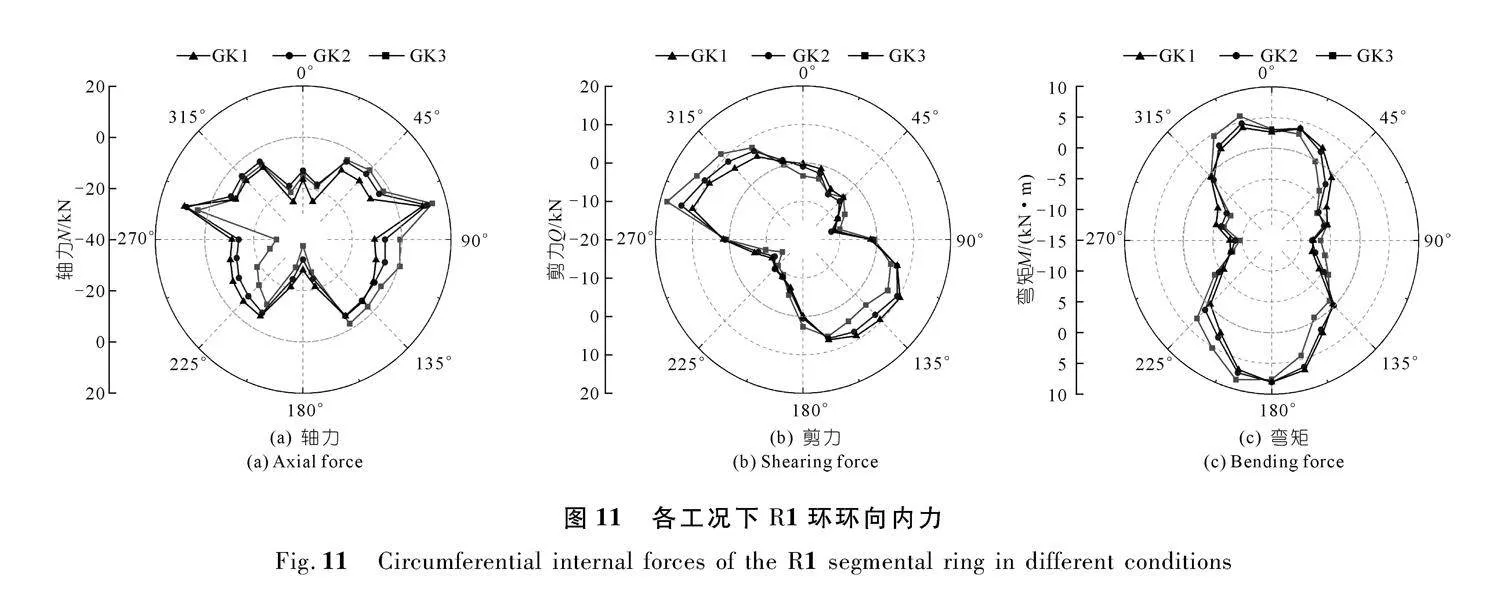
由于盾尾第1环衬砌直接承受千斤顶推力，因此顶推力对R1环衬砌的影响最为显著。图10为各工况下R1环衬砌横向弯矩（Mx）和竖向弯矩（My）变化曲线，图11为各工况下R1环衬砌环向内力分布曲线。由图可见，相比于对盾尾环环向内力的影响，顶推力引起的盾尾衬砌横向和竖向弯矩更为明显。在均匀顶推力作用下盾尾管环仅受推进油缸的挤压作用，不会在纵向产生附加弯矩，因此其对隧道的承载性能是有益的，可以提高盾构隧道的纵向刚度。

由图10可见，随着GK2和GK3中水平方向和竖直方向2组油缸推力偏差越来越大，其引起的横向弯矩和竖向弯矩也随之增大，GK2中非对称推力引起的横向弯矩和竖向弯矩分别为2 940 kN·m和1 670 kN·m，而GK3中非对称推力引起的横向弯矩和竖向弯矩分别增大至4 660 kN·m和6 910 kN·m。

由图11可见，非对称推力对盾尾R1环衬砌的环向内力有一定影响，但由于横向不受力，因此各工况下R1环衬砌环向内力值均较小。由图可见，随着各组油缸间推力偏差的不断增大，偏心推力对环向内力极值的影响也不断增大。相比于GK1，GK2和GK3中R1环环向轴力最大值分别增加15%和34%，环向剪力最大值分别增加28%和65%，环向弯矩分别增加11%

和21%，可见偏心推力对环向剪力的影响较大。

3.3" 管片应力

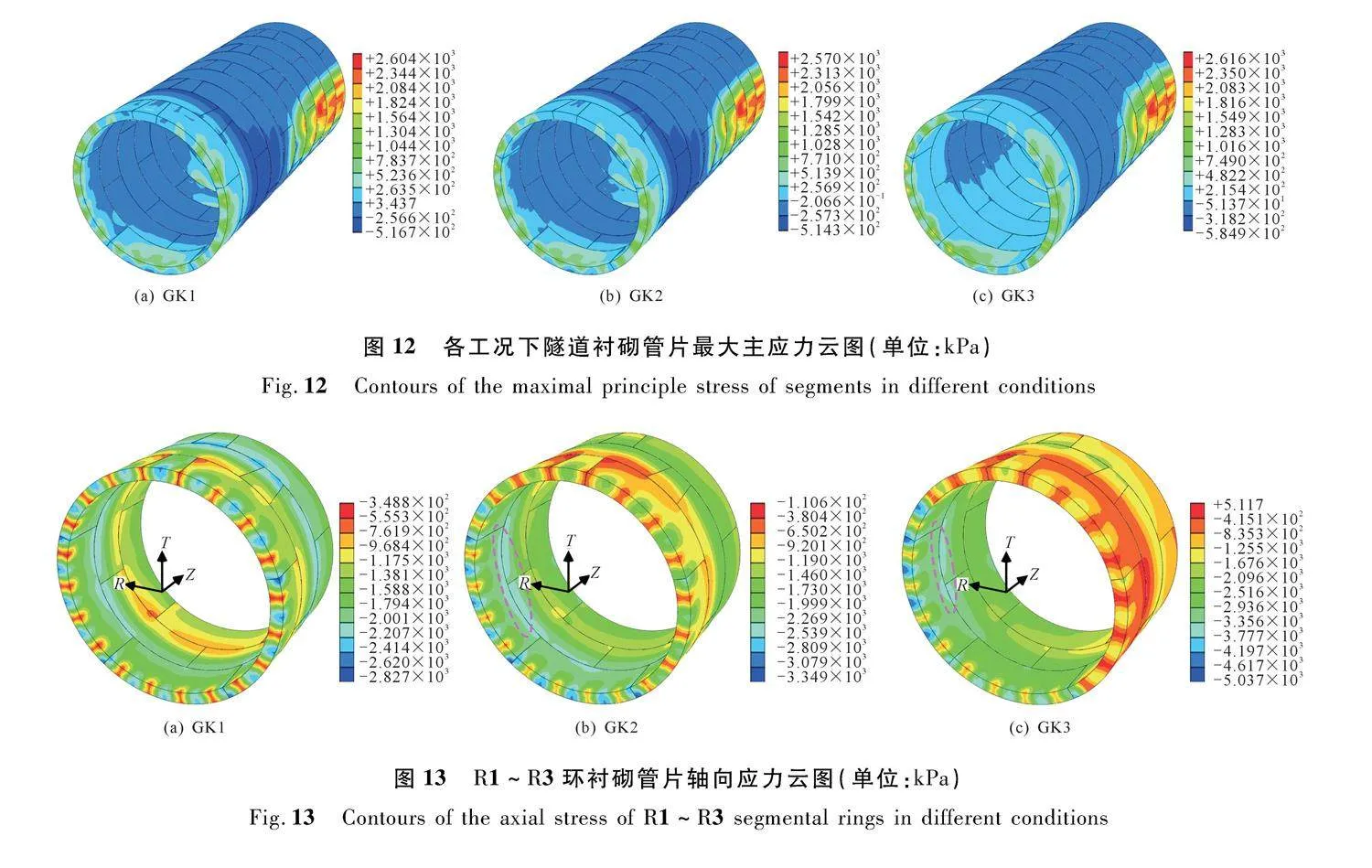
图12为各工况下隧道衬砌管片最大主应力云图。由图可见衬砌管片拉应力主要位于盾尾第1环和第6～10环水土压力作用段。由于在水土压力作用段，管片衬砌发生了较大的收敛变形，因此在该范围内，拱腰管片外侧及拱顶、隧底内侧混凝土出现拉应力，最大拉应力发生在拱腰处，各工况下最大拉应力基本一致，约为2.6 MPa。

图13为盾尾第1环至第3环管片轴向应力（σ33）云图。由图可见，由于盾尾第1环管片在纵向直接承受盾构推进油缸压力，其轴向基本处于全断面受压的状态。但随着推进油缸压力偏差的逐渐增大，小荷载侧轴向压应力逐渐减小，局部管片混凝土逐渐处于纵

向受拉状态。此外，由图13（b）和13（c）可知，在偏心推力作用下，大荷载侧盾尾2环衬砌间出现局部压应力集中现象（图中红色椭圆标识处），尤其在第1环和第2环衬砌“T”形接缝处，压应力集中现象更加明显，随着两侧推力差的进一步增大，T形接缝处压应力集中范围进一步减小，而应力值明显增大，GK2和GK3中接缝处最大轴向应力分别为-2.59 MPa和-3.68 MPa。

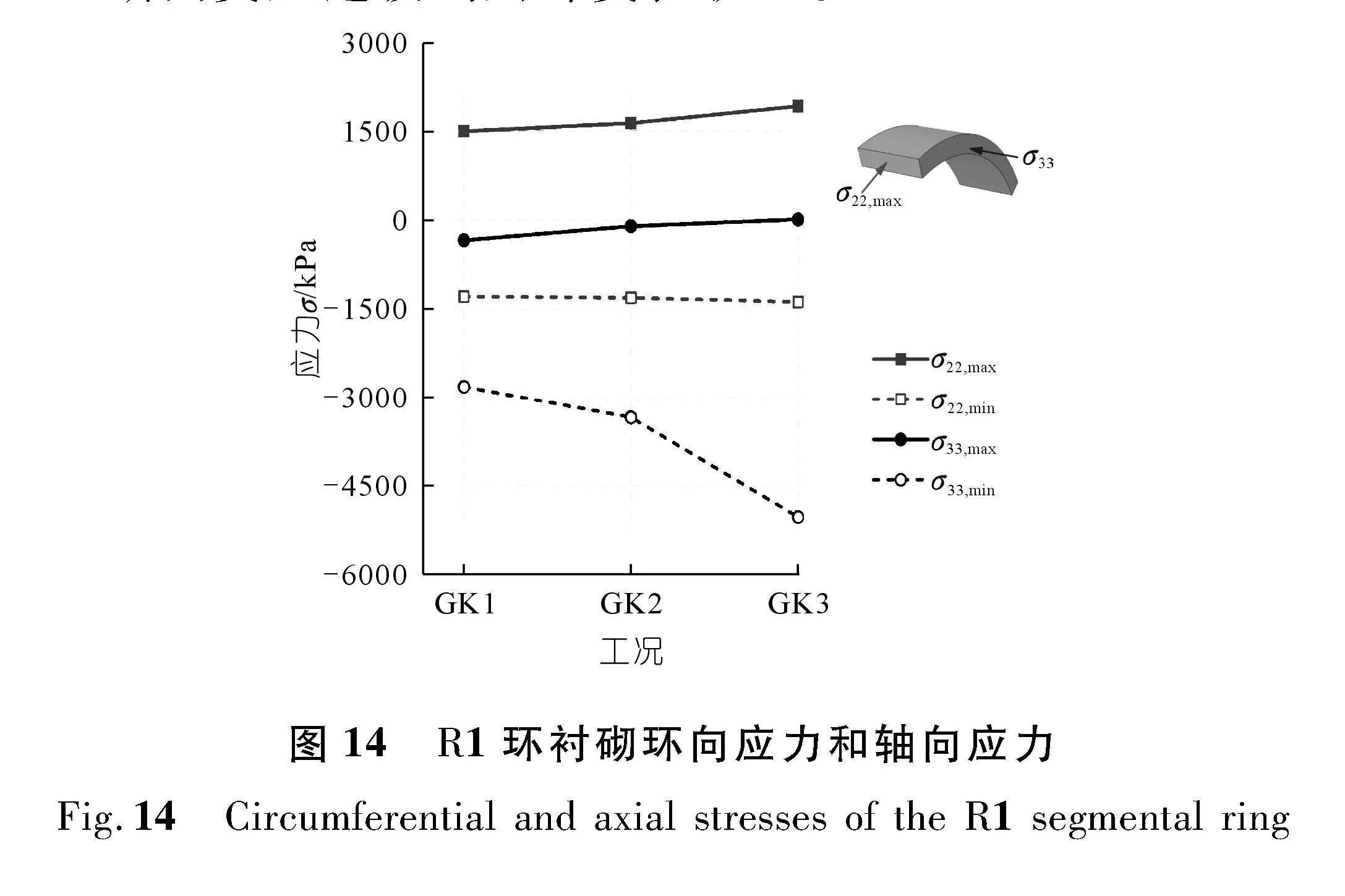
图14为盾尾第一环衬砌在不同工况下环向应力（σ22）和轴向应力（σ33）极值的变化情况，其中正值表示拉应力，负值表示压应力。由图可见，随着各组油缸推力偏差的不断增大，R1环衬砌环向应力极值也随之增大，环向拉应力的增长较环向压应力的增长明显。

从最大轴向应力（σ33，max）的变化情况来看，随着各组油缸推力偏差的不断增大，衬砌纵向应力状态逐渐由全断面受压过渡到局部受拉状态。

3.4" 螺栓内力

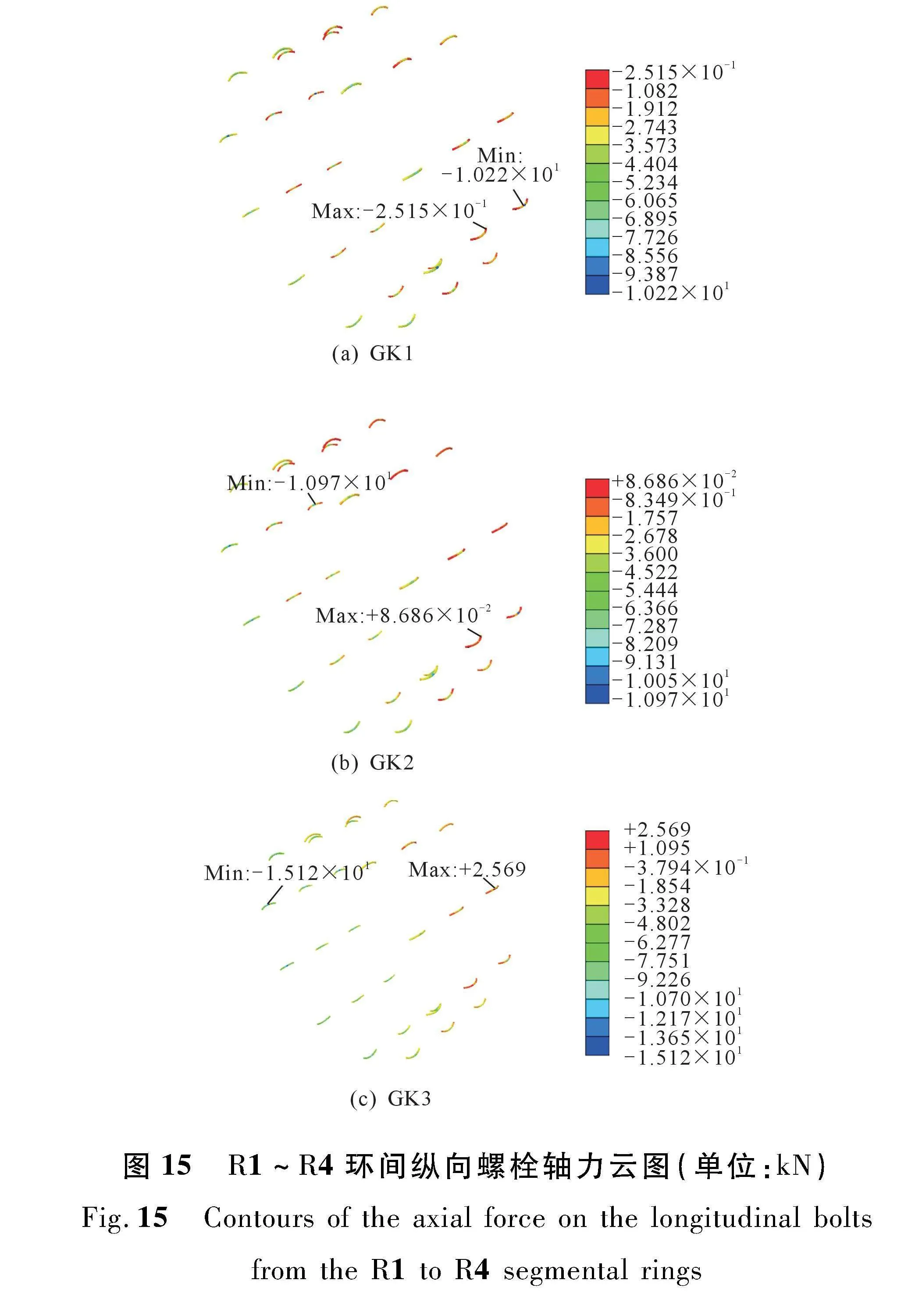
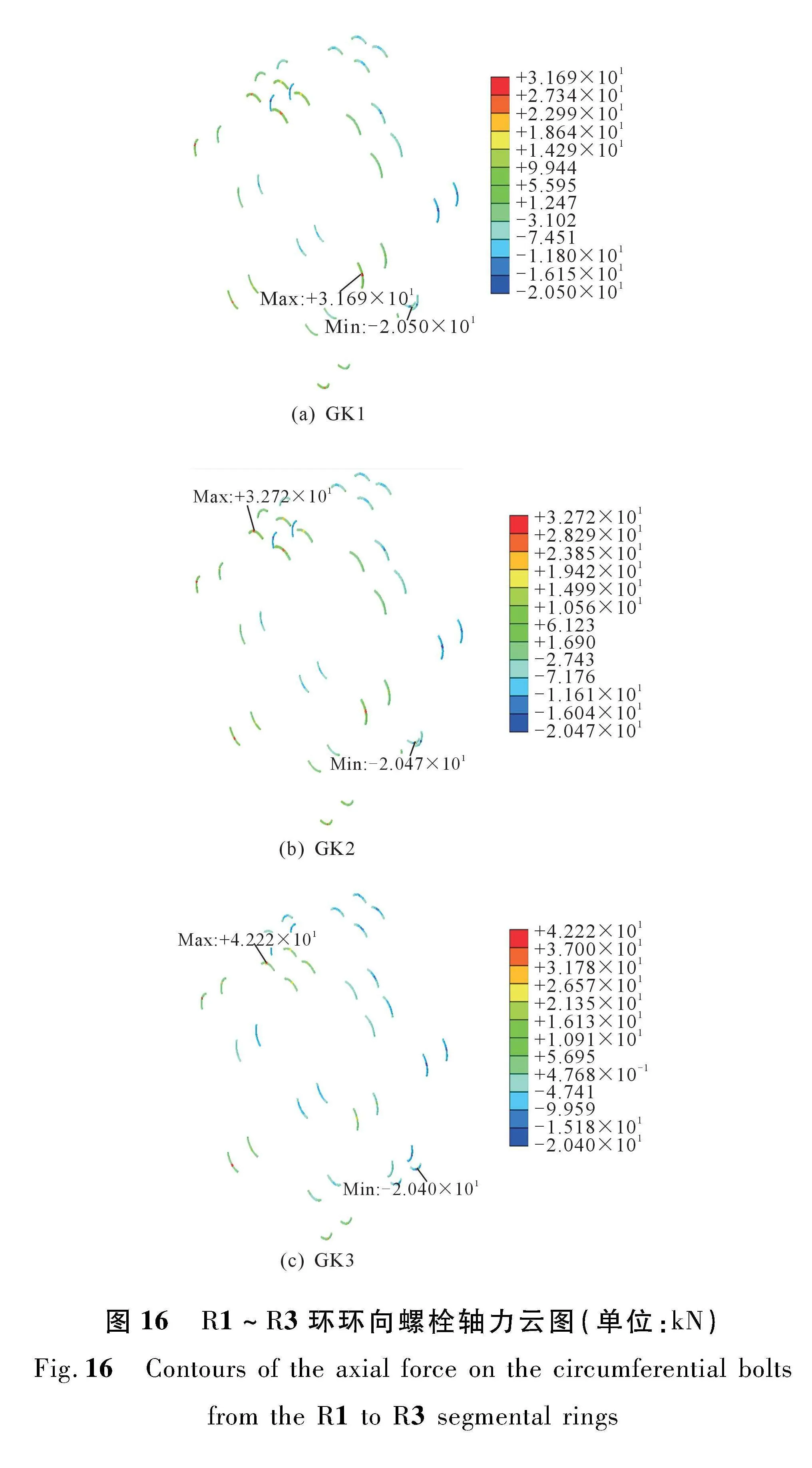
图15和16分别为盾尾第1～4环间纵向螺栓轴力云图和盾尾第1～3环内环向螺栓轴力云

图，其中正值表示螺栓受拉，负值表示螺栓受压。由图可见：① 随着盾尾各组油缸推力差异的不断增大，盾尾已拼装衬砌中环、纵向接头螺栓的拉力均有所增大。② 在均匀顶推力作用下（GK1工况），纵向接头螺栓均承受压力（图15（a））；而在非均匀推力作用下，小荷载侧（A、D组油缸所在区域）

部分纵向螺栓开始受拉，且推力差异越大，纵向螺栓拉力也越大（图15（b）和图15（c）），表明在此工况下部分环向接缝有受拉张开趋势。

③ 环向螺栓压力未随纵向推力变化而发生显著改变，但随着各组油缸推力偏差的增大，环向螺栓拉力却有所增大，且环向螺栓最大拉力均位于盾尾第1环衬砌内，这主要是由于随着各组推力差异的增大，盾尾第一环衬砌发生了显著的椭变（图8），使得部分环向螺栓受拉。

4" 结 论

本文以圭峰山隧道区间盾构隧道曲线施工工程为背景，建立了盾构隧道施工期精细化有限元模型，采用数值方法研究了非对称推力作用下已拼装衬砌的力学响应特性，得到以下结论。

（1） 在偏心推力作用下，盾尾衬砌发生非对称变形，其横向变形表现为衬砌管片向大荷载侧的挤出变形。非对称推力的影响范围与荷载偏心量相关，本文荷载条件下，盾构在直线段和曲线段掘进时，非对称推力的影响范围分别为盾尾后5环和7环管片。

（2） 非对称推力作用下隧道横向弯矩和竖向弯矩增长明显，使得隧道纵向处于压弯状态。相对而言，非对称对盾尾环环向内力的影响较小，且主要体现为对其环向剪力的影响。

（3） 衬砌管片的应力分析表明，管片混凝土拉应力极易达到管片混凝土的受拉强度，表明本文模型采用的混凝土损伤塑性模型能更好地反映衬砌管片的受力性能。

（4） 盾构沿曲线掘进时，大推力侧盾尾管片T形接缝处会产生压应力集中现象，若此处存在拼装误差则极易造成管片混凝土的压溃；而在小推力侧，随着推力偏差的增大，部分纵向螺栓开始受拉，可能会导致管片环缝防水失效。因此，盾构在曲线段施工时更应严格控制管片拼装质量，加强盾尾衬砌环缝渗漏水监测。

参考文献：

［1］" 何川，封坤，方勇.盾构法修建地铁隧道的技术现状与展望［J］.西南交通大学学报，2015，50（1）：97-109.

［2］" 叶飞，何川，王士民.盾构隧道施工期衬砌管片受力特性及其影响分析［J］.岩土力学，2011，32（6）：1801-1808.

［3］" 竺维彬，鞠世健.盾构隧道管片开裂的原因及相应对策［J］.现代隧道技术，2003，40（1）：21-25.

［4］" 秦建设，朱伟，陈剑.盾构姿态控制引起管片错台及开裂问题研究［J］.施工技术，2004，33（10）：25-27.

［5］" 焦齐柱，万波，门燕青，等.盾构施工中不利工况下隧道结构的力学行为［J］.地下空间与工程学报，2016，12（5）：1308-1314.

［6］" 苏昂，王士民，何川，等.复合地层盾构隧道管片施工病害特征及成因分析［J］.岩土工程学报，2019，41（4）：683-692.

［7］" 日本土木学会.隧道标准规范（盾构篇）及解说［M］.朱伟，译.北京：中国建筑工业出版社，2001.

［8］" TAJIMA H，KISHIDA M，FUKAI N，et al.Study on construction loads during shield tunneling using a three-dimensional FEM model［J］.Tunnelling and Underground Space Technology，2006，21（3）：250-256.

［9］" 张鹏.盾构隧道管片施工力学性能三维数值模拟研究［J］.铁道工程学报，2012（10）：63-69.

［10］ZHOU J H，WU D，S H，et al.Analysis on damage cause of shield tunnel segments during construction［J］.Advanced Materials Research，2012，594：13081313.

［11］CHO S H，KIM J，WON J，et al.Effects of jack force and construction steps on the change of lining stresses in a TBM tunnel［J］.KSCE Journal of Civil Engineering，2017，21（4）：1135-1146.

［12］CHAIPANNA P， JONGPRADIST P.3D response analysis of a shield tunnel segmental lining during construction and a parametric study using the ground-spring model［J］.Tunnelling and Underground Space Technology，2019，90：369-382.

［13］王士民，于清洋，彭博，等.基于塑性损伤的盾构隧道双层衬砌三维实体非连续接触模型研究［J］.岩石力学与工程学报，2016，35（2）：303-311.

［14］艾辉军，彭立敏，施成华.基于三维非连续接触模型的管片接头静动力特性分析［J］.岩土工程学报，2013，35（11）：2023-2029.

［15］中华人民共和国住房与城乡建设部.混凝土结构设计规范：GB 50010-2010［S］.北京：中国建筑工业出版社，2010.

［16］庄茁，由小川，廖剑晖.基于ABAQUS 的有限元分析和应用［M］.北京：清华大学出版社，2009.

［17］ABAQUS Inc.ABAQUS 2016 Documentation，Version 2016.SIMULIA.

［18］张占廷，刘宇锋.ABAQUS 中的混凝土塑性损伤模型［J］.建筑结构，2011，41（增2）：229-234.

［19］刘巍，徐明，陈忠范.ABAQUS混凝土损伤塑性模型参数标定及验证［J］.工业建筑，2014（增1）：167-171.

［20］闻邦椿.机械设计手册：连接与紧固［M］.北京：机械工业出版社，2007.

［21］日本土木学会.盾构隧道管片设计：从容许应力设计法到极限状态设计法［M］.官林星，译.北京：中国建筑工业出版社，2012.

［22］国家铁路局.铁路隧道设计规范：TB 10003-2016［S］.北京：中国铁道出版社，2017.

（编辑：郭甜甜）

Responses of shield tunnel structure under action of asymmetric thrust

YU Guowu1，LIANG Guanglin2，QI Jun1，LIU Qiqing1，ZHANG Lingzhi1

（1.GuangdongZhuzhao Railway Co.，Ltd.，Guangzhou 510000，China；" 2.School of Aeronautics and Astronautics，Sun Yat-sen University，Shenzhen 518107，China）

Abstract：

To investigate the effects of asymmetric shield thrust on the mechanical properties of a tunnel structure during small radius curved advancing，a refined finite element model of the shield tunnel in Guifeng Mountain was established.The numerical model employed a damaged plastic constitutive model of concrete considering the nonlinear properties of the segmental lining.The mechanical behavior of the shield tunnel under asymmetric thrust was systematically analyzed using the established numerical model.The results showed that ：① the cross-sectional deformation of the segment adjacent to the tail of the shield exhibits extrusion deformation towards the heavy load side under asymmetric thrust；② the vertical and transverse bending moments，induced by the asymmetric thrust，on the shield tunnel are much larger than those along the circumferential direction.Additionally，the influence of asymmetric thrust on the circumferential shear force on the tunnel is significant.③ the mechanical state of the shield tunnel along the longitudinal direction is transferred from a whole-section compression state to a compression-bending state thanks to the pressure difference between different thrust jacks.A dramatic concentration of compressive stress occurs at the circumferential joints of segmental rings on the side with larger thrust，particularly at the T-shaped joints.The concrete of the segmental lining can easily crack in this area if there are assembly errors in the segments.Additionally，the longitudinal bolts embedded in the circumferential joint on the side with smaller thrust will gradually be in tension as the pressure difference among the thrust jacks increases.This keeps some circumferential joints in a state of tension，leading to a potential risk of waterproof failure in the shield tunnel.Therefore，when a shield drives along a curved alignment，the pressure of the different thrust jacks should be adjusted rationally，the assembly quality of the segmental lining should be strictly controlled，and the monitoring of seepage in the joints of the shield tunnel should be enhanced.

Key words：

shield tunnel； driving in curved alignment； asymmetric thrust； concrete damage plasticity model； numerical simulation； Guifeng Mountain tunnel