基于运行灵活性的配电网扩展规划方法研究

摘 要：清洁能源在电力供应中的渗透率逐年提高，导致电网中出现较多的灵活性资源，如何充分调动清洁能源、控制电网扩展和运营成本是目前需要解决的问题。本文提出基于运行灵活性的配电网扩展规划模型，该模型由2层结构组成，规划层以综合投资成本最低为控制目标，运行层以电网运行状态最佳为控制目标，并兼顾配电网规划质量和扩展、运营成本。完成建模后，本文将一个32节点的配电网作为算例，对其应用效果进行验证。结果显示，与传统的配电网规划方法相比，本文提出的规划模型有效降低了配电网扩建费用和运行费用，显示出良好的应用价值。

关键词：配电网；运行灵活性；扩展规划模型

中图分类号：TM 715" " 文献标志码：A

随着清洁能源发电占比持续提高，配电网的不确定因素不断增加。风力发电、光伏发电具有较高的灵活性，对配电网扩展设计的影响较大。传统的规划方式难以适应该变化，需要一种具有运行灵活性的规划方法，可充分调动新能源发电资源，降低电网的扩容范围和总成本，并满足负荷需求。

1 基于运行灵活性的配电网扩展规划模型构建

1.1 数学模型构建

基于运行灵活性的配电网扩展规划模型包括2层，分别为规划层和运行层。这种双层架构方式既考虑了源荷的不确定性，又能保证运行控制的灵活性，其数学模型分别如公式（1）、公式（2）所示。

（1）

式中：f1（x）为规划层的成本目标函数；minf1（x）为扩建投资成本最低；x为待求的网架0-1扩展变量；h1（x，µ*）为约束上层规划层的条件；µ*为配电网运行层传递的参数，与主动控制要素相关；g1（x，µ*）为模型需要满足的等式约束条件。

（2）

式中：f2（µ）为规划层的运行状态目标函数；max minf2（µ）为系统运行状态最佳；y为配电网中的不确定因素；φ为不确定要素y的变化区间；以运行状态最优为目标，h2（x*，µ，y）为模型上层规划层需要满足的不等式约束条件；x*为规划层传递的网架扩展参数；µ为待优化的运行参数；以运行状态最优为目标，g2（x*，µ，y）为模型需要满足的等式约束条件[1]。

在以上模型中，由规划层产生网架扩展方案，并将其传递至运行层。与此同时，运行层生成优化的运行参数，再提供给规划层。双层模型相互配合，实现配电网灵活性规划。

1.2 上层规划层模型构建

上层规划层模型由多个要素组成，除了目标函数外，还包括投资约束条件、安全约束条件以及配电网潮流，根据该模型求解网架规划相关的0～1的变量。在传统模式下，升级改造既有配电网时，以电源和配电网负荷为基础，计算出配电网容量和净负荷，再结合电网的电压等级确定升级改造方案。随着新能源发电占比不断提高，新扩建的配电网大量并入风电、光伏发电，不确定因素显著增加，对配电网的灵活性提出了更高要求[2]。

在网架规划中，经济性是重要的考虑因素，其取决于网架扩展时的投资建设成本和建成后的运行成本，2类成本之和称为综合投资成本，以综合投资成本最小化为目标，相应的数学描述方法为minC=minCinv+Cop。其中，C为综合投资成本，Cinv为配电网扩展投资建设成本，Cop为扩建部分的运行成本。配电网扩展投资建设成本的计算方法如公式（3）所示。

（3）

式中：KL为馈线成本的回收系数；CL为单位长度馈线的投资成本；hL ij为馈线hij的长度；yij为馈线hij的二元投资变量。

当yij=0时，代表线路投资无变动；当yij=1时，代表规划年内需要进行投资扩容。参数馈线成本回收系数根据规划周期和折现率进行计算。

配电网的运行成本与储能电站数目、购电单位成本、储能电站单位成本、网络损耗以及可中断负荷数量相关。在上层规划层模型中，潮流解精度要求较低，因此可忽略其对模型的影响，潮流的约束条件如公式（4）所示。

（4）

式中：Uj，t为馈线节点j在时刻t的电压幅值；Ui，t为馈线节点i在时刻t的电压幅值；rij为馈线hij的电阻；xij为馈线hij的电抗；Pij，t为馈线hij在时刻t的有功潮流；Qij，t为馈线hij在时刻t的无功潮流；i和j为馈线起点和终点的节点编号；ΨL为配电网馈线的集合；Uref 为参考电压幅值；T为调度周期。

1.3 下层运行层模型构建

下层运行层模型的目标函数具有较多的约束条件，包括储能系统、电网安全、分布式电源出力、可中断负荷以及上级电网的馈入功率。以系统最优运行状态为目标，运行层模型的待求变量为配电网主动控制影响因素的运行参数。随着电网负荷增加，该模型的运行控制能满足扩容需求，同时降低扩容带来的投资成本。

下层运行层模型能够充分调动系统中的灵活性资源，并控制运行场景下的净负荷曲线，经过其优化，负荷曲线更平滑。优化结果上传至上层规划层模型后，根据运行反馈结果改进配电网的规划方案。运行层的最优状态以净负荷总量最低为目标，相应的目标函数数学描述方法如公式（5）所示。

（5）

式中：Pnel 为节点i在时刻t的净负荷；Ψ N为配电系统的节点集合。

参数Pnel 的计算方法如下：节点i在时刻t的有功功率+节点i在时刻t的储能系统充电功率-节点i在时刻t的分布式电源上网有功功率-节点i在时刻t的可中断负荷中断容量-节点i在时刻t的储能系统放电功率[3]。

该模型具有一系列约束条件，以上级电网馈入功率约束条件为例，其数学表达式如公式（6）所示。

（6）

式中：Pinj 为节点i在时刻t的上级电网馈入的有功功率；Pmax 为节点i在时刻t的上级电网馈入的最大有功功率；Qinj 为节点i在时刻t的上级电网馈入的无功功率；Qmax 为节点i在时刻t的上级电网馈入的最大无功功率。

2 模型求解方法和实例分析

2.1 模型求解方法

2.1.1 最恶劣运行场景的提取

本文提出的配电网规划模型由2个部分组成，其目标函数、待求变量、约束条件和数据量均较多且数据的量纲并不统一，配电网的运行参数在24h内变化幅度较大，以上问题增加了模型求解的难度[4]。另外，在运行层模型中，部分问题的计算存在耦合情况，难以进行求解。为了提高模型求解的可操作性，运用概率多场景分析方法生成较多数量的运行场景，再从这些场景中提取运行条件最恶劣的一种，该场景即代表全天负荷削减总量最大。此时，运行层模型转化为公式（7），降低了模型的求解难度。公式（7）将公式（2）进行了简化，实现了耦合问题的解耦，为正常求解创造了便利的条件。

（7）

2.1.2 模型求解流程

根据上述原理，可建立以下模型求解流程。1） 模型初始化，输入规划周期和数据。2） 通过多场景生成方法生成一定数量的差异化场景，场景数量记为Ns。3） 对场景进行遍历，计算每个场景下的全天负荷削减量，将削减量最大的场景确定为最恶劣场景。4） 将待优化的运行参数µ设置为零，以最恶劣的运行场景为前提，求解规划层优化模型。根据模型的求解结果，确定配电网的扩建方案。5） 根据规划层形成的扩建方案，对网架和约束条件进行修正，再分析求解运行层模型，使系统运行状态达到最佳[5]。6） 运行层模型求解的结果为设备运行方案，基于该方案修正新的最恶劣场景。7） 在新的最恶劣场景下重复以上步骤。8） 计算相邻2次规划层模型求解结果的差异，当其小于阈值时，停止迭代计算。

2.2 实例分析

2.2.1 算例模型参数

本文选取的算例模型由32个节点组成，其电压等级和基准容量分别为20kV、1MVA。该系统扩容后，最大载流量从200A提升至500A，运行调度时长设计为24h，上级电网馈入模型的最大功率设置为25MW。整个模型由1条主线和12条并联支线组成，支线的编号为F1～F12。根据顺序，支线上的节点数量分别为4、2、2、2、2、3、3、2、4、4、2和2个，线路、节点和设备间的关系见表1。风力发电设备、光伏发电设备、可中断负荷和储能系统接入特定的节点，设备与接入节点的关系见表2。在电力成本方面，购电价格为0.5元/kW·h，可中断负荷的补贴价格为0.3元/kW·h，储能装置的运行成本为0.67元/kW。32个节点共计形成31条馈线，每2个节点间的线路为1条馈线。其长度、电阻和电抗存在较大差异。

2.2.2 配电网扩展规划模型参数设置

在算例分析阶段，需要设置配电网扩展规划模型的初始参数，将折现率设置为1%，规划场景中数据间隔时间取值为1.0s，单位长度馈线的投资成本取值为100.275万元/km，节点i在时刻t的上级电网馈入的最大有功功率取值为0.4MW，可中断负荷的最大调用时长设置为10h。

2.2.3 最恶劣运行场景的提取

在该算例中，配电网的规划周期设置为10年，预计用电负荷的年增长速率为7%，不考虑光照强度和风速在规划周期内的变化，即认为这2项因素基本维持不变。运用概率多场景分析方法生成10个不同的运行场景，计算出每个运行场景下的全天负荷削减量[6]。对场景进行编号，记为1～10。其中，场景1的全天负荷削减总量最大，计算结果为98.86kW。在该场景下，光伏功率在7：00—16：00保持稳定，达到1.0MW。风电负荷在24h内的变化区间为0.5MW～0.98MW。系统有功负荷在0：00—4：00和20：00—24：00较高，在4：00—20：00时段内有功负荷先降低、后增大，最小值约为0.5MW。

2.2.4 规划效果分析

根据该模型输出和线路规划结果显示，在规划年内，需要扩容的馈线为1-2、2-3、13-14、1-13、1-25和1-29，配电网规划效果分析过程如下。

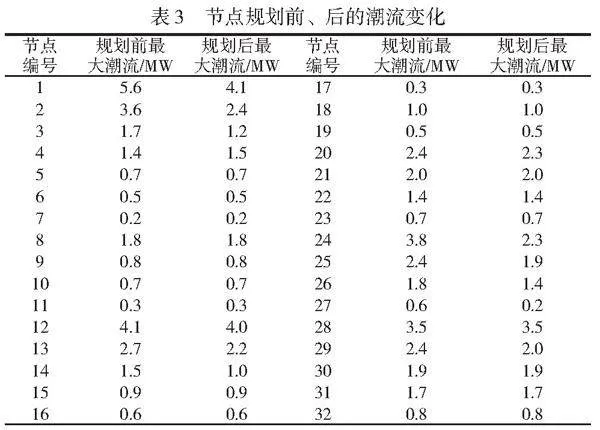
2.2.4.1 配电网潮流控制效果分析

以下对比线路中的前20个节点规划前、后的潮流变化见表3。模拟数据显示，在配电网扩容规划后，节点1、2、3、13、14、24、25、26、27和29的潮流明显下降，原因是这些节点对应的线路引入了可调节的灵活性资源，例如风机、光伏发电设备，其他节点未安装灵活性装置，因此潮流在规划前、后基本保持不变。配电网线路对潮流大小的设置有限值，显然，规划后配电网潮流整体降低，有利于提升配电网的运行效果。

2.2.4.2 灵活性资源优化调度效果分析

对于储能设备的运行状态，模拟结果显示，储能设备在0：00—8：00处于连续放电阶段，放电功率为0.4MW。8：00以后，储能设备的剩余容量和放电电流快速下降，放电功率在9：00降为0。可见，目标网架在初始阶段充分调动了储能装置，有效降低了0：00—8：00时段的全网净负荷。

上级电网馈入容量用于平衡全网净负荷。运用本文建立的模型扩展配电网模拟规划后配电网在24h内的上级电网馈入容量，结果显示，馈入容量呈现出先降低、后增大的趋势，12：00—14：00的上级电网馈入容量最低，对应的数据为8.2MW。由变化趋势可知，由于引入了具有灵活性的可再生电源，配电网对上级电网的依赖性有所下降。

2.2.4.3 经济性分析

在传统规划模式下，以满足配电网总负荷需求为目，并预留一定的负荷变化空间，预留负荷通常为预计负荷需求的10%～20%[7]。比较传统规划方案和本文规划模型的扩建费用和运行费用，结果见表4。由模拟数据可知，基于运行灵活性的配电网扩展规划方法比传统规划方法节约了51.609万元，经济效益良好。

3 结论

新能源发电方式在电力供应中的占比持续提高，与传统发电方式不同，新能源发电缺乏稳定性，导致电网中的不确定因素有所增加。为了在新的背景下提高电网规划的质量，本文提出基于运行灵活性的配电网规划方法，并得出以下结论。1） 该规划模型由上层规划层和下层运行层组成，上层规划层模型以综合投资成本最小化为目标，下层运行层模型以电网运行状态最佳为控制目标，通过上、下层模型的配合优化电网的扩展规划效果。2） 运用32节点的配电网模型检验该规划方法，与传统规划方法相比，在满足负荷需求的前提下，本文方法的扩容线路更少、投资建设成本大幅降低且运行成本基本持平。该规划模型有效提高了电网运行的独立性，降低了对上级电网的依赖，并能充分调动灵活清洁发电资源。

参考文献

[1]石铖，安锐，高红均，等.基于柔性多状态开关和动态重构的配电网灵活运行方法[J].电力系统保护与控制，2023，51（22）：133-144.

[2]李宗晟，张璐，张志刚，等.考虑柔性资源多维价值标签的交直流配电网灵活调度[J].电工技术学报，2024，39（9）：2621-2634.

[3]王利利，王皓，任洲洋，等.计及灵活资源调节潜力的高压配电网新能源接纳能力评估[J].中国电力，2022，55（10）：124-131.

[4]董冰冰，陈子建，陈维江，等.配电网用灵活控制特快速开关方案及其触发导通特性[J].高电压技术，2022，48（5）：1808-1816.

[5]任智君，郭红霞，杨苹，等.含高比例可再生能源配电网灵活资源双层优化配置[J].太阳能学报，2021，42（9）：33-38.

[6]雷才嘉，贾巍，高慧，等.一流城市配电网的灵活适应性评价指标及计算方法[J].供用电，2019，36（5）：2-7.

[7]曹子健，林今，宋永华.含分布式电源及灵活负荷的配电网电量合约市场[J].电网技术，2019，43（7）：2430-2440.