基于MSBWO优化LSTM的短期风电功率预测

摘 要：本文针对风电当并网时风电功率不稳会影响整个地区总网内的电压稳定的问题，建立以优化长短期记忆神经网络（Long-Short Term Memory，LSTM）超参数、提升风电功率的预测精度为目标的优化模型，提出基于多策略改进的白鲸优化算法（Multi-Strategy Beluga Whale Optimization，MSBWO）的求解方法。利用电力集团真实风力发电数据预测数据集1号风机数据来验证所提模型的可行性。试验结果表明，本文提出的方法能够获得更优解，收敛速度更快，预测效果更好。

关键词：风电功率预测；白鲸优化算法；长短期记忆网络

中图分类号：TK 89" " " " " " " " 文献标志码：A

研究者对风电功率预测做了大量研究，深度学习模型具有从原始数据中提取复杂模式的良好能力，因此备受关注。长短期记忆神经网络（Long Short Term memory，LSTM）的专门化结构设计有效规避了模型训练中的梯度爆炸或消失问题，成为在风电功率预测等时间序列分析领域最流行的算法之一。LSTM模型有参数设置烦琐的问题，采用智能优化算法进行超参数寻优成为解决神经模型参数设置烦琐的方法之一。唐杰等[1]引入粒子群优化算法对双向LSTM预测模型的超参数进行优化，加快模型收敛速度，提高模型预测精度。史彭珍等[2]建立了蝴蝶优化算法，优化最小二乘来对向量机的风电功率进行短期预测。上述智能算法存在搜索空间维度较低、算法结构复杂、内部参数较多以及寻优精度有限等问题。综上所述，本文提出基于多策略改进的白鲸优化算法（Multi-Strategy Beluga Whale Optimization，MSBWO）的求解方法，使用该方法建立以优化LSTM超参数来提升风电功率的预测精度为目标的优化模型。对实测数据进行仿真，仿真结果验证了模型的预测精度更高。

1 白鲸优化算法（BWO）

白鲸优化算法（Beluga Whale Optimization，BWO）是由大连理工大学的ZHONG C T等学者[3]于2022年提出的一种元启发式优化算法，模拟了白鲸的游泳、捕食和鲸落行为。该算法将优化过程划分为探索、开发和鲸落3个阶段，并引入平衡因子Bf和白鲸坠落概率Wf这2个自适应变量。平衡因子Bf的作用是完成从探索至开发阶段的过渡，白鲸坠落概率Wf的作用是判断是否进入鲸落阶段。

Bf和Wf对算法的控制决策和探索能力起决定性作用，当平衡因子Bflt;0.5时，白鲸进入开发阶段；反之，进入探索阶段。随着迭代次数T增大，进入开发阶段的概率随之增大。当Bflt;Wf时，白鲸进入鲸落阶段。

1.1 探索阶段

在探索阶段，同步或镜像近距离游泳的一对白鲸共同决定位置的更新，其数学模型如公式（1）所示。

（1）

式中：XT+1 为第i条白鲸在j维度更新后的位置；T为当前迭代次数；XT 为第i条白鲸在Pj维度中的位置，Pj（j=1，2，…，d）为从d维中选取的随机数；XT 为从种群中随机选取的第r条白鲸；r1、r2为增强搜索阶段的随机算子，均为（0，1）的随机数；sin（2πr2）、cos（2πr2）模拟镜像白鲸的鳍朝向水面。根据奇数odd和偶数even选择维度，更新后的位置信息显示2条白鲸游泳和跃出水面的同步或镜像行为。

1.2 开发阶段

BWO算法的开发阶段受到白鲸捕食行为的启发，白鲸可以根据其周围白鲸的位置进行移动和觅食，其之间也会交换位置信息以合作寻找食物源。为了增强算法的收敛性，在BWO算法的开发阶段引入Levy飞行策略。Levy飞行策略的数学模型描述如公式（2）所示。

XiT+1=r3XT best-r4XiT+C1⸱LF（XrT-XiT） （2）

式中：XiT+1为第i条白鲸的新位置；r3、r4为（0，1）的随机数；XT best为种群中白鲸的当前最佳位置；C1为随机跳跃度，其作用是衡量Levy飞行的强度；LF为符合Levy分布的随机数，表示飞行策略；XrT为1条随机白鲸的当前位置；XiT为第i条白鲸的当前位置。

LF的计算过程如公式（3）所示。

LF=0.05×（（u×σ）/|v|1/β） （3）

式中：u、v为正态分布随机数；σ为u对应的正太分布的标准差； β为默认的常数，β=1.5。

σ的计算过程如公式（4）所示。

（4）

1.3 鲸落阶段

在优化过程中，白鲸可能迁徙至其他地方，也可能发生鲸落并坠入深海。当平衡因子Bflt;Wf时，白鲸进入鲸落阶段。在鲸落阶段，白鲸利用当前位置和鲸落下坠的步长建立位置更新公式，如公式（5）所示。

XiT+1=r5XiT-r6XrT+r7XTstep （5）

式中：r5、r6和r7为（0，1）的随机数；XTstep为白鲸步长，其计算过程如公式（6）所示。

（6）

式中：ub、lb分别为优化问题的上界和下界；Tmax为最大迭代次数；C2为与白鲸下降概率和种群大小有统计学意义的步长因子，其计算过程如公式（7）、公式（8）所示。

C2=2Wf×N" " " " " " （7）

（8）

式中：Wf为白鲸坠落的概率，从初始迭代的0.1下降至最后一次迭代的0.05，说明在优化过程中，当白鲸与食物源更接近时，白鲸的危险降低；N为种群规模。

2 多策略改进的白鲸优化算法（MSBWO）

标准BWO算法具有良好的寻优能力，但是在解决复杂优化问题的过程中存在收敛速度慢、全局探索能力不足以及易陷入局部最优的问题[4]。本文针对BWO提出多个方面改进，以提高种群初始解的质量，提高算法的全局收敛性，即多策略改进的白鲸优化算法（Multi-Strategy Beluga Whale Optimization，MSBWO）。

2.1 初始化种群改进

BWO采用随机生成初始种群的方法，种群容易分布不均匀，会导致种群多样性减少，种群质量不高，减慢算法的收敛速度。混沌映射具有随机性、非重复性和混沌遍历性等特点，与依赖概率的随机生成相比，其更能够使种群分布均匀，因此可以利用混沌映射生成初始种群来增加潜在解的多样性。文献中常用的混沌映射有Logistic映射、Tent映射和Circle映射等，Circle映射更稳定，其混沌值覆盖率高[5]，考虑Circle映射当取值为 [0.2，0.6] 时较为密集，因此对Circle映射公式进行改进[6]，使其更加均匀。原Circle 映射计算过程如公式（9）所示。

（9）

式中：xn+1为映射后的第n+1个种群数据点；mod为求余函数；xn为第n个种群数据点。

改进后的Circle映射计算过程如公式（10）所示。

（10）

2.2 精英池策略

由上述BWO原理可知，当BWO在开发阶段和鲸落阶段进行位置更新时，总是使用当前最佳个体作为食物源，如果食物源已陷入局部最佳，那么后续所有个体都将聚拢于局部最佳个体，导致算法早熟收敛。为增强种群多样性，灰狼优化算法（Grey Wolf Optimization，GWO）提出等级制度，将当前最佳的3个头狼的算术平均作为最佳位置，以避免使用1个最佳个体引导造成的缺陷。因此，受GWO启发，本文引入精英池策略，将当前最佳的前3个个体以及3个个体的加权平均作为精英池中的候选精英，当进行位置更新时随机从精英池中选择1个个体作为引导，提高算法跳出局部最佳的能力。

2.3 融合自适应Levy飞行与螺旋搜索的开发阶段

标准BWO的开发阶段采用固定步长的Levy飞行以提高其收敛能力，在算法的不同阶段，其期望的Levy飞行步长可能会有所不同。Levy飞行的步长α越大，越容易搜索到全局最优解，但是搜索精度降低；α越小，搜索精度越高，但是搜索速度减慢，公式（3）中0.05是其步长。因此，为增强算法对解空间的探索能力，提高其收敛精度，本文采用自适应的Levy步长策略。在迭代前期Levy飞行步长较大，能够探索解空间的广度范围；在迭代后期 Levy飞行步长递减，探索过程更精细。由BWO开发阶段的位置更新公式（2）～公式（4）可知，其虽然涉及随机个体、最佳个体和当前个体，但是对解空间的探索存在漏洞。在白鲸优化算法中，白鲸个体在搜寻猎物的过程中会根据目标位置（即最佳位置）与自身位置之间的螺旋形状调整每次位置更新的移动距离，这种策略能够极大程度地利用区域信息，提高搜索能力，因此本文引入该策略，以提高算法在局部空间开发方面的严密性与准确性，增强局部搜索能力。

综上所述，融合自适应Levy飞行与螺旋搜索的开发阶段的位置更新如公式（11）所示。

XiT+1=r3⸱EleteT-r4XiT+C1⸱LF（XrT-XiT）⸳|EliteT-XiT|cos（EliteT-XiT）⸱ebl " " " " " " " " " " " " " " " " " " " " " " " " （11）

式中：EliteT为当前随机从精英池中选择的最优解；ebl为螺旋形状搜索参数；b为对数螺旋形状常数；l为 [-1，1] 的随机数。

LF的计算过程如公式（12）所示。

（12）

式中：为自适应指数步长。

2.4 黄金正弦策略

黄金正弦算法（Golden Sine Algorithm，Golden-SA）基于正弦函数与单位圆的关系，能够遍历正弦函数中的所有点，即单位圆中的所有点，因此具有较强的全局搜索能力。该算法在位置更新过程中引入黄金分割系数，使算法在每次迭代过程中都能够对可能产生优秀解的区域进行充分搜索，加快了算法的收敛速度，有助于跳出局部最优解。

本文采用黄金正弦策略对BWO种群进行更新，以增强BWO的全局搜索能力，加快算法的收敛速度。改进后鲸落阶段的位置更新如公式（13）所示。

XiT+1=XiT+1|sinR1|+r1sin（2πr2）|x1⸳EliteT-x2XiT " " " " " " " " " " " " " （13）

式中：R1为[0，2π]的随机数；x1、x2为黄金分割系数，其作用是缩小搜索空间，引导个体向精英收敛。其计算过程如公式（14）、公式（15）所示。

x1=α⸳（1-τ）+b⸱τ （14）

式中：α为搜索起始位置，即优化问题的下界；τ为黄金比率，τ=；b为搜索结束位置，即优化问题的上界。

x2=α⸳τ+b⸱（1-τ） （15）

3 MSBWO优化LSTM的短期风电功率预测模型设计

本文对BWO进行4个方面改进后，提出MSBWO算法，MSBWO算法流程如图1所示。

基于MSBWO优化LSTM的短期风电功率预测具体步骤如下。1）数据预处理。采用四分位法识别功率异常点，提高数据质量。2）超参数寻优。使用MSBWO优化LSTM的4个超参数，适应度函数为LSTM的平均绝对误差（Mean Absolute Error，MAE）。3）基于MSBWO优化LSTM风电功率预测。使用步骤（2）优化的4个超参数设置LSTM模型参数，构建LSTM预测模型。4）模型评判。使用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、MAE和均方根误差（Root Mean Square Error，RMSE）评价指标分析预测结果，评判模型效果。

4 实例分析

为验证MSBWO优化LSTM的短期风电功率模型的优越性，采用Python 3.9进行编程。选取真实风力发电数据预测数据集1号风机的风电数据，以15 min为1个采样点，共34 589个采样点。本文划分前70%的数据用于训练模型，后30%的数据用于测试。

4.1 MSBWO-LSTM模型超参数优化过程

采用MSBWO、BWO和PSO 3种优化算法分别对LSTM的迭代次数、2层隐藏层的神经元个数以及学习率共4个超参数进行寻优，构建LSTM模型对风电功率进行预测。优化算法的种群规模N设置为15，最大迭代次数Tmax为20，在试验中采用的对比算法的参数设置与原文献一致，适应度函数为平均绝对误差。4个超参数的寻优搜索范围见表1。

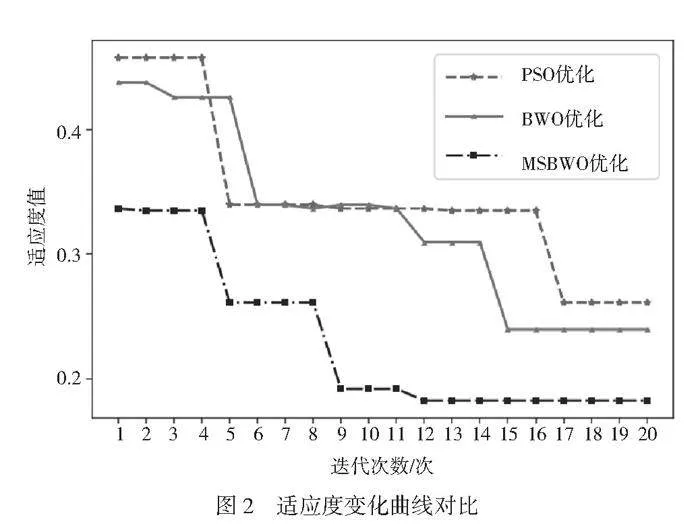
3种群体智能优化算法对 LSTM 寻优过程的适应度变化曲线对比如图2所示。

4.2 预测结果分析

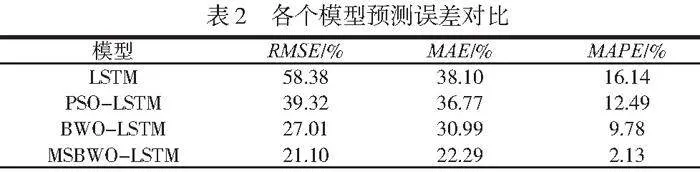
根据MSBWO算法的寻优结果对LSTM参数进行配置。在划分的测试集中进行仿真测试，并与单一LSTM模型、PSO-LSTM模型和BWO-LSTM模型进行对比。各个模型预测误差对比见表2。由表2可知，使用优化算法对LSTM模型进行超参数寻优可以提升LSTM模型的预测效果，PSO-LSTM、BWO-LSTM模型比单一LSTM模型的RMSE分别降低了32.64%、53.73%，MAE分别降低了3.49%、18.66%，MAPE分别降低了22.61%、39.40%。使用多策略改进的BWO优化LSTM模型（MSBWO-LSTM）比BWO-LSTM模型的RMSE、MAE和MAPE分别降低了21.88%、37.75%和78.22%。说明MSBWO-LSTM能够有效提升风电功率的预测效果。

5 结论

本文提出使用多策略改进的MSBWO对LSTM进行超参数寻优，以提升风电功率的预测精度。主要采用改进的Circle映射以增加BWO种群的多样性，增强了算法的全局搜索能力；引入精英池策略，提高BWO跳出局部最优的能力；采用自适应的Levy步长策略，提升了BWO的收敛速度；在鲸落阶段引入黄金正弦策略，加快了算法的收敛速度。实例分析结果表明，本文采用多策略对BWO进行改进，提出基于 MSBWO 建立优化模型，其目标为优化 LSTM超参数来提升风电功率的预测精度，成功提高了预测精度和准确性。

参考文献

[1]唐杰，李彬.基于EMD-PSO-BiLSTM组合模型的短期风电功率预测[J].自动化应用，2024，65（5）：126-129.

[2]史彭珍，魏霞，张春梅，等.基于VMD-BOA-LSSVM-AdaBoost的短期风电功率预测[J].太阳能学报，2024，45（1）：226-233.

[3]ZHONG C T，LI G，MENG Z.Beluga whale optimization：A novel"nature-inspired metaheuristic algorithm [J]. Knowledge-Based systems，2022（251）：109215.

[4]陈曦明，张军伟.融合FDB策略和切线飞行的改进白鲸优化算法[J].计算机时代，2023（11）：46-51.

[5]黄杨杨.属性Logistic混沌映射下的物联网隐私数据安全共享[J].现代电子技术，2024，47（13）：97-101.

[6]ZHANG D M，XU H，WANG Y R，et al. Whale optimization algorithm for embedded circle mapping and onedimensional oppositional"learning based small hole imaging[J]. Control and Decision，2021，36（5）： 1173-1180.

基金项目：湖南省教育科学研究工作者协会2024年度高校课题“基于深度学习模型的高职智慧课堂的构建策略与应用研究”（项目编号：XJKX24B241）；湖南环境生物职业技术学院校情专项课题“计算机应用技术专业（五年制中高职衔接）人才培养方案建设研究”（项目编号：XQ2023-58）。