基于爬山算法的地铁系统功耗监控技术

摘 要：地铁系统是能量消耗较大的复杂系统。为了有效降低地铁系统的能量消耗，本文针对其功率曲线的监控问题，提出了一种基于爬山算法的监控方法。根据地铁系统功率曲线随速度变化不断调整的实际情况，爬山算法能够在低速、中速和高速功率曲线上进行持续监控和搜索。在搜索过程中，本文重点设计了爬山算法的搜索方向和搜索步长，并深入分析了搜索方向与搜索步长的关系。在仿真环境下，进行了爬山算法对功率曲线的监控效果测试。测试结果表明，随着地铁系统变速调整，爬山算法可以有效地进行持续跟踪，并将实际功率调整到最佳功率点。

关键词：地铁系统；功率消耗；爬山算法

中图分类号：U 231 " " 文献标志码：A

地铁是非常重要的城市内循环交通方式，可以极大地缓解地面交通压力。地铁运输不仅载客容量大，而且运输速度快、运输效率高[1]，因此地铁是一线城市、新一线城市，甚至部分有建设条件的二线城市的重要运输方式。从能量消耗的角度看，地铁自身质量较大，是电能、机械能等多系统交织的复杂系统，因此需要消耗大量能量来维持运行[2]。为了有效降低地铁能耗，必须对地铁运行过程中的功率进行监控。经验数据表明，复杂系统的最低能耗均有对应的最佳功率点。因此，地铁系统功耗监控过程中的重点就是如何监控其功率运行曲线，使其一直运行在最佳功率点或者接近最佳功率点的位置[3]。地铁系统的功率变化曲线是一条峰、谷特征明显的曲线，最佳功率点一般位于波峰或波峰附近。针对该特点，本文构建爬山算法，使地铁系统的功率一直处于或接近最佳功率点，从而提升地铁系统的功率效率。

1 爬山算法的设计

以电能为主的各种能量消耗决定了地铁系统的能量利用率。为了有效降低地铁系统的能耗，应该使地铁系统持续运行在最佳功率点位。经验数据表明，最佳功率点处于接近最大功率点的位置，并不是处于低位的功率点。在最佳功率点上运行，地铁系统的运行效率高、能量损耗低。因此，在地铁动态运行过程中，对最佳功率点进行持续搜索是功耗监控的关键所在。

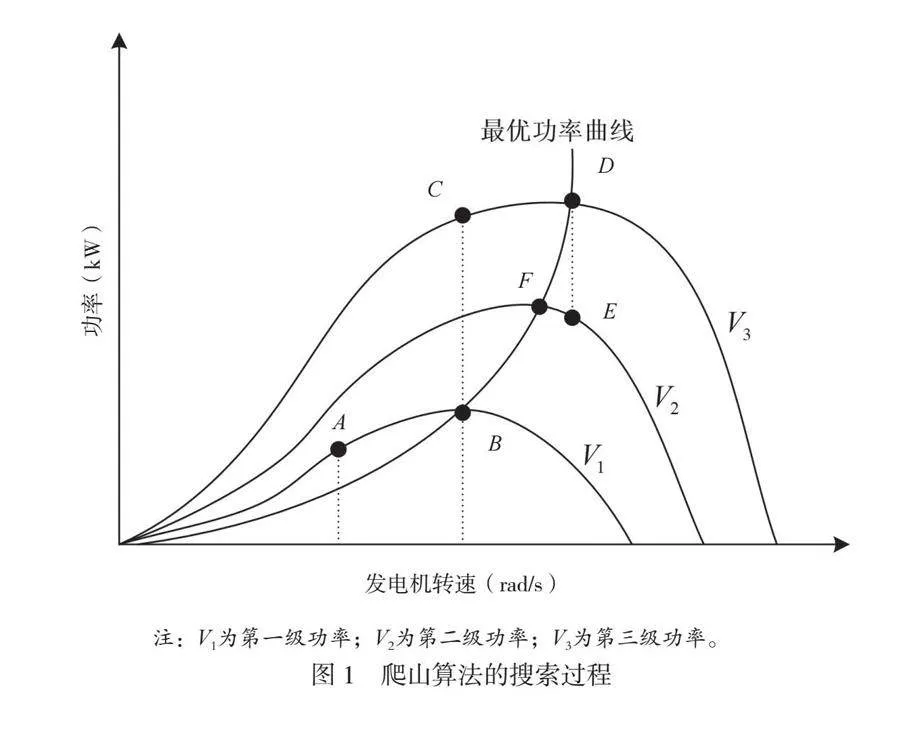
在功率寻优的各种算法中，爬山算法具有非常重要的地位。在当前位置处，爬山算法会沿着功率曲线持续搜索。该搜索过程具有相对稳定的步长，并按照一定的搜索方向，沿着功率曲线不断寻找最佳功率点的位置。如果搜索方向不正确，爬山算法会自动调整方向。如果搜索步长过大，可能会越过最佳功率点，需要执行反向搜索来发现最佳功率点。可见，搜索步长和搜索方向的合理配置对爬山算法的性能实现具有非常重要的影响。爬山算法的最佳功率点搜索过程如图1所示。

图1以发电机转速-功率曲线来表征爬山算法的控制对象，一共给出了3条曲线，分别代表不同位置的功率变化曲线。越向上方，功率曲线的绝对数值变化区域越大。从最下方的曲线可以看出，爬山算法会从功率点A位置进行搜索，逐渐找到B点所在的最佳功率点。如果发电机在这种状态下保持运行，爬山算法会稳定在B点，以使整个系统持续获得最佳功率。但是当发电机功率曲线突变到最上方曲线时，B点在垂直方向上对应的功率点C就不是新功率曲线的最佳功率点。爬山算法会再次启动，进而找到D点所在的最佳功率点。同理，如果发电机功率曲线再次突变到中间曲线时，那么D点在垂直方向上对应的功率点E就不是新功率曲线的最佳功率点。爬山算法会反向搜索，进而找到F点所在的最佳功率点。

可见，随着系统运行状态的改变，最佳功率点也在不断变化，从而形成一条最佳功率点变化曲线，即图1中的B、F和D点所构成的曲线。

上述过程同样适用于地铁系统。地铁启动后以中低速运行，对应一条功率变化曲线。进而地铁系统会拉升到高速运行状态，也对应一条功率变化曲线。即将停靠时，地铁系统会减速，对应一条相对低速的功率变化曲线，直至停靠。地铁系统的变速过程如图2所示。

可见，地铁系统并不会一直以一个稳定的速度值运行，因此整个地铁系统所需功率处于动态波动和持续变化中。地铁车辆按照启动、运行、加速、加速运行和减速停靠的物理状态循环演进。在该过程中，地铁的速度也从0变化到低速，从低速变化到高速，从高速变化到低速，再从低速变化到0。地铁车辆的速度不同，所需牵引力做功也不同，导致地铁系统所需功率并不一致。为了满足地铁不断变速、调整的需要，需要对其能量系统进行有效控制，不断改变其实际运行功率。这种改变的终极目标是调整地铁功率，使其在动态运行过程中一直运行在最佳功率点的位置。

根据图2所示的地铁系统的变速过程，需要采用爬山算法，对功率曲线进行持续跟踪、监控，不断寻找最佳功率点，有效减少地铁系统的功耗。在最佳功率点的搜索过程中，需要合理设计搜索距离即搜索步长。本文设计分为3种方面。

第一，当“爬山算法”向右侧寻找新的最大功率点时，操作的数学模型如公式（1）所示。

（1）

式中：P（n）为功率曲线上n点对应的功率大小；α为转速调整参数；kwo为地铁系统功率调整参数。

第二，当“爬山算法”向左侧寻找新的最大功率点时，操作的数学模型如公式（2）所示。

（2）

式中：β为用于转速调整的参数。

第三，设定搜索方向，主要是判断当前的搜索方向是否正确，数学模型如公式（3）所示。

（3）

在搜索距离的配置下，“爬山算法”会比较当前功率和一个搜索距离上的功率，如果二者的差值ΔPgt;0，就说明新搜索位置上的功率比原来位置上的功率大，搜索方向正确。如果二者的差值ΔPlt;0，就说明新搜索位置上的功率比原来位置上的功率小，搜索方向需要更改，进行反向搜索是正确的。

在不断判断搜索方向的过程中，如果Δw（n）的变化非常微弱，就表明搜索过程可以终止了。

在本文设计的爬山算法中，搜索步长和搜索方向的关系如图3所示。由图3可知，采取小步长的搜索速度较慢，但是越过最佳功率点的概率较低。大步长的搜索速度更快，但是可能会出现越过最佳功率点、继续反向搜索的情况。因此，需要合理配置搜索步长和搜索方向，才能取得最佳搜索效果。

2 爬山算法的性能测试

地铁系统是一个复杂系统，为了适应其运行过程中的速度变化，其功率曲线一直处于不断跃升、变迁的状态。因此，爬山算法需要在不同功率曲线上进行最佳功率点寻优。本文给出了地铁系统功率曲线跃迁的状态，进而针对其不断变速、调整的情况，设计了爬山算法，重点对爬山算法的搜索方向和搜索步长进行了合理设置。下文将进行试验，以验证爬山算法的有效性。

试验将地铁系统纳入一个仿真环境中，测试电气系统运行所需的最佳功率。在仿真环境下，设定地铁系统电气模块所需的最佳功率点为2500W，其初始工作状态为500W。爬山算法需要从初始状态不断向最佳功率点进行搜索。

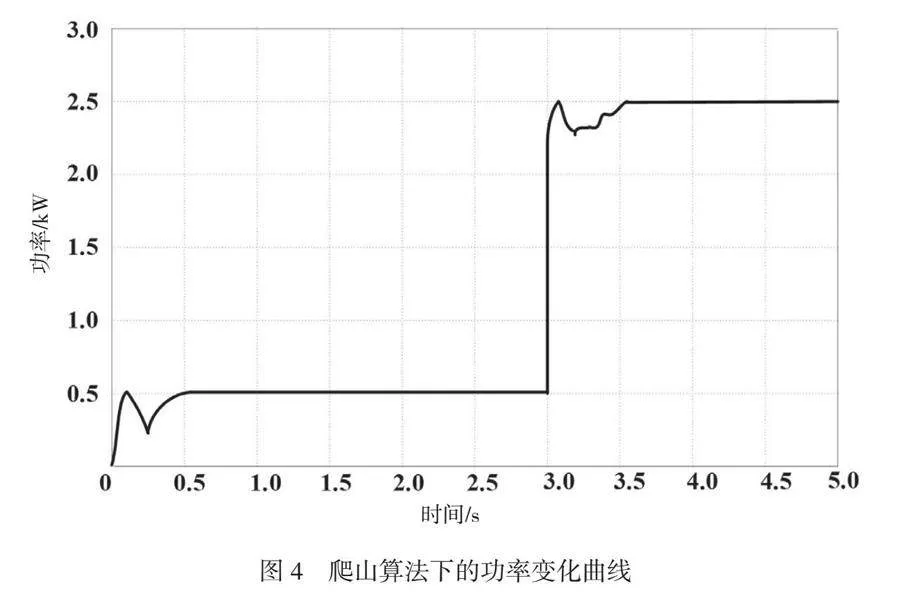
爬山算法在持续的寻优过程中，会对功率曲线进行有效监控、跟踪，并将地铁系统电气模块的初始500W迅速拉升至2500W的最佳功率点。但是，该过程可能存在起伏变化。仿真环境下的功率曲线跟踪观察结果如图4所示。

地铁系统启动电气模块后，以较短的时间进入500W的初始工作状态，其后出现0.5s左、右的短时波动，进而进入较平稳的持续状态。但是500W并不是地铁系统电气模块的最佳功率点位，这时采用爬山算法，可以将其拉升到最佳功率点。爬山算法持续搜索，找到最佳功率点，并且当第3.0s时将功率曲线拉升至2500W的位置。由于拉升前、后功率曲线存在较大的功率差，因此系统需要经过短时间波动，才能稳定工作在2500W状态下，即达到地铁系统的最佳功率点。

除了功率曲线的变化外，试验还观察了整个功率控制过程中占空比的变化。在传统“爬山算法”运行过程中，对应于电气系统的0.5kW工作功率，占空比为0.30～0.45；对应于电气系统的2.5kW工作功率，占空比为0.48～0.60。可见，同功率的变化曲线情况相似，传统“爬山算法”的占空比变化不稳定，并且波动的时间更长。本文改进“爬山算法”控制下的地铁电气系统占空比变化情况如图5所示。

由图5可知，在改进“爬山算法”的控制下，对应于电气系统的0.5kW工作功率，占空比为0.33～0.36；对应于电气系统的2.5kW工作功率，占空比为0.56～0.60。可见，与传统“爬山算法”相比，本文算法控制下的占空比波动范围更小。

3 结论

地铁是重要的城市内循环交通方式，可以极大缓解地面交通压力。地铁运输不仅载客容量大，而且运输速度快、运输效率高。从能量消耗的角度看，地铁自身质量较大，是电能、机械能等多系统交织的复杂系统，因此需要消耗较多能量来维持运行。为了有效降低地铁能耗，必须监控地铁运行过程中的功率。本文针对地铁功耗的实际情况，构建了爬山算法，并在功率曲线上持续搜索最佳功率点。仿真环境下的测试结果表明，采用本文提出的爬山算法，可以准确得到地铁系统的最佳功率点，并使地铁系统持续运行在最佳功率点位。

参考文献

[1]赵红宇，杨壁贤，钟子峰，等.基于地铁车辆功率设备的温度传感器性能检测装置研究与应用[J].电子制作，2023，31（24）：102-105.

[2]陶子渝，汪益敏，邹超.基于阻抗和功率守恒法的地铁车辆段上盖建筑车致振动预测模型研究[J].振动与冲击，2022，41（7）：58-65.

[3]闵杰.地铁车辆段分布式光伏发电并网功率控制方法研究[J].江苏科技信息，2024，41（1）：128-131.